MFG： 集中線の解説

渦巻きっぽい集中線を作るフィルタを実装してみたくなった。

以前集中線は作った事があるので、その応用で良さそう。だけれど集中線がどんなだったかをもう忘れているので、それを思い出す必要がある。

という事でコードを見直すにあたり、ブログにしておこうと思う。

コードを眺める

まずはサンプル集のコードを持ってきて、リソースを文字列に置き換えると大体以下のようなコードになっている。

@title "集中線"

# Specify width by ratio of I.
@param_f32 TR(SLIDER, label="幅",  init=0.5, min=0.1, max=1.0)
@param_f32 WRR(SLIDER, label="幅ランダム",  init=0.2, min=0.0, max=1.0)
@param_f32 DR(SLIDER, label="密度", init=0.5, min=0.01, max=1.0)
@param_f32 LR(SLIDER, label="長さランダム",  init=0.2, min=0.0, max=1.0)
@param_pos ORIGIN(POINTER, label="中心")

let PI = 3.141592
let N_MAX = 400
# Number of lines. Interval is 2PI/N
let N = f32(N_MAX)*DR
let I = 2.0*PI/N


# Shorter edge of canvas (width or height).
let SIDE = f32(min(*input_u8.extent()))

# Start line from about half of shorter edge.
let OFFSET = SIDE/4.0

# N random number, but N is not known  in advance, so create N_MAX.
@bounds(N_MAX, 2)
def RAND_TABLE |x, y| { rand() }

# return positive region theta.
fn atan2p |y: f32, x: f32| {
  let theta = atan2(y, x)
  ifel(theta > 0.0, theta, 2.0*PI+theta)
}

def result_u8 |x_0, y_0| {
  # ORIGIN to pixel pos.
  let fo = ORIGIN*f32(input_u8.extent())
  let fxy0 = f32[x_0, y_0]

  @bounds(3, 3)
  def occupy |xi, yi| {
    let fxy = fxy0 - [0.33, 0.33] + 0.33*f32[xi, yi]

    let [rx, ry] = fxy - fo

    let theta = atan2p(ry, rx)

    # Index of I.
    let A = round(theta/I)
    # Basic angle of this pos.
    let ATheta = A*I
    let AI = i32(A)


     # Width of line, stands for the angle of triangle. Randomness is added for each A.
     let T = TR*(1.0-WRR*RAND_TABLE(AI, 0))*I

     # Length of origin. Away from OFFSET+random.
     let RO = OFFSET*(1.0+2.0*LR*RAND_TABLE(AI, 1))

     # to: Origin of triangle
     let to =  fo + RO* [cos(ATheta), sin(ATheta)]

     let txy = fxy - to
     let ttheta = atan2p(txy.y, txy.x)

     ifel(abs(ttheta-ATheta) < T/2.0, 1.0, 0.0)
  }

  let avg_occupy = rsum(0..<3, 0..<3) |rx, ry| { occupy(rx, ry) }/9.0
  u8[0x0, 0x0, 0x0, round(255.0*avg_occupy)]
}

えーと、N_MAX個の乱数テーブルを作っているな。

# N random number, but N is not known  in advance, so create N_MAX.
@bounds(N_MAX, 2)
def RAND_TABLE |x, y| { rand() }

そしてavg_occupyと言っているので、スーパーサンプリングでアンチエイリアスしているのか。

  let avg_occupy = rsum(0..<3, 0..<3) |rx, ry| { occupy(rx, ry) }/9.0

occupyの中は真面目にコードを読む必要がある。 コードの中にいく前に、ロジック的な事を考えてみたい。

どの三角形の区画に所属しているか

GPUプログラムなので、与えられた点から考え始めないといけない。

ある点x0, y0が与えられた時に、これは三角形に入っているか？入っていたた黒、入っていなければ透明、というのが基本的な考え方になる。

ランダムさをどう考えているか、というと、どうも幅と長さだけがランダムで、各三角形の中心は一定間隔のようかな。

とすると、中心の点と線の本数からキャンバス全体が区画に分けられるか。

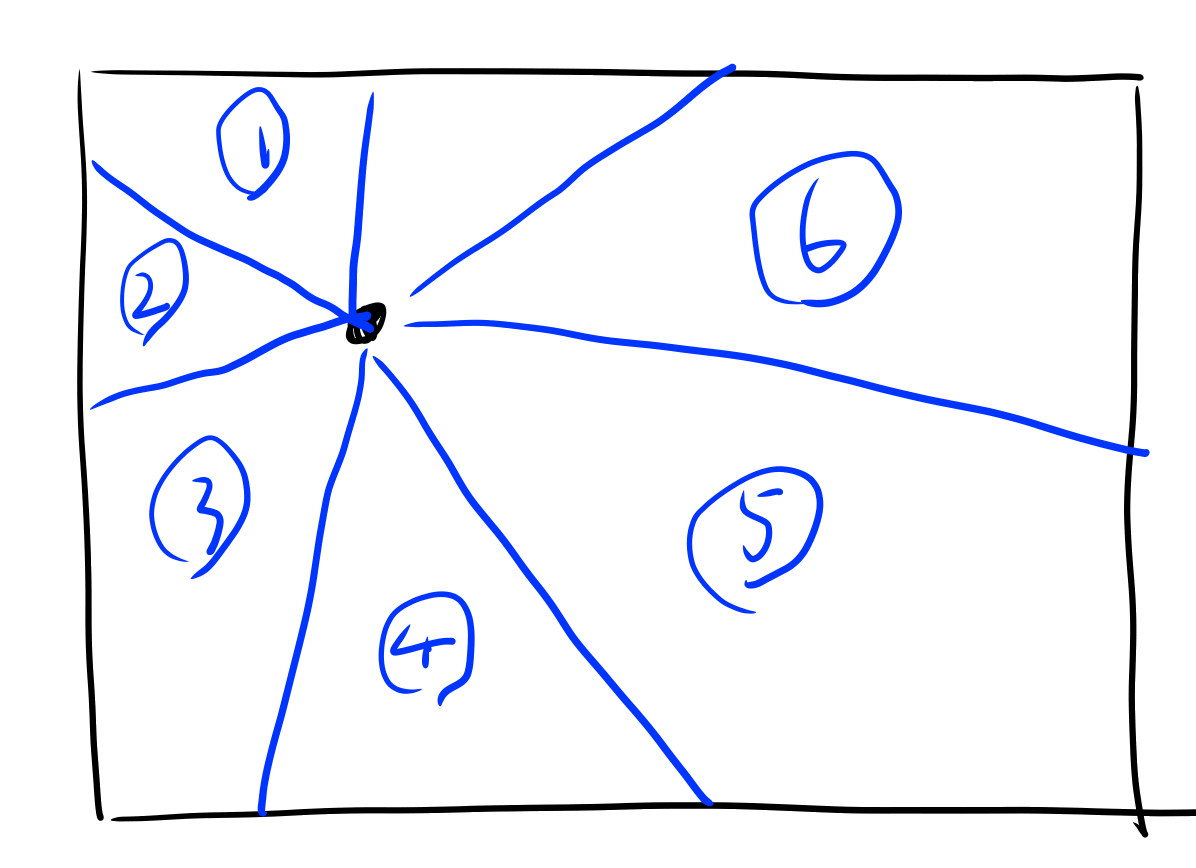
この青の数字の幾つか、という区画をまず調べて、 この区画の中心から見た座標系で考えて三角に入っているか、というのが、ロジカルには一番単純だな。

計算としては三角形の頂点から始めて中に入っているかを見る方が多分簡単だけど、 ここでは考え方にフォーカスしたいので、ひとまず中心から考えた座標系を考えたい。

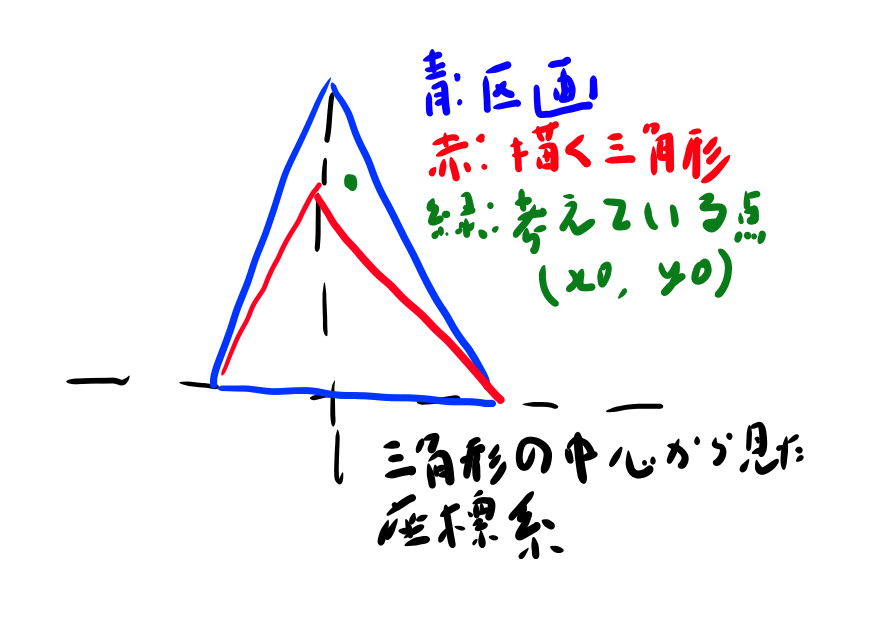
この座標系で考えた時に三角形の中にあるか外にあるか、を考えれば良さそう。 そして三角形の幅と長さにランダムさがあるようなので、 幅と長さがパラメータのようだ。

幅と長さが与えられた時に、緑の点が三角形の中にあるか外にあるか？というのがナイーブに考えた問題っぽい。

頂点から考える

ナイーブに考えた結果を、もう少し計算が容易になるように考えると、区画まで考えたら頂点と二つの辺を見て、その中にあるかを外積で判定する方が良さそうだ。 これはGPUで三角形を描く定石でもある。

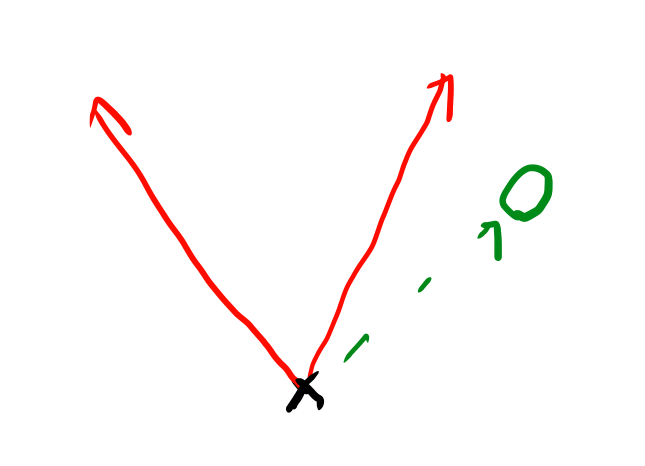
頂点から見て、対象の点が三角の中かどうかは二つのベクトルとの外積を求めて、符号が同じなら外、符号が変われば中と判定出来そう。 このへんの話は以前MFGで基本図形を描いてみよう（後編）に書いた。

けれど今回の限定された状態なら、もっと簡単に出来そう。 外積を使うまでも無く、角度が赤の範囲の外だったら外、と結論づけられる気もする。

三角形の幅と長さがパラメータになっているのだから、パラメータからこの頂点の位置ベクトルは出すことができて、三角形の二辺のなす角度も求まりそう。 あとは目的の点へのベクトルがどの角度にあるかを調べれば良さそう。

アルゴリズムとコードを対応づける

以上の考えで大体集中線を描くロジックは理解出来た気がする。 ロジックとコードを対応づけていきたい。

ロジックの流れ

以上の理解をまずは整理しておく。

1. 中心からの角度で区画に分けて、どの区画にいるかを決める
2. その区画の三角形の頂点を求める
3. 頂点を基準に二つの辺のカバーする角度の範囲を求める
4. 頂点から目的の点へのベクトルのなす角度を求める

こういう流れになってそう。 あとはコードの対応関係を見ていこう。

最初の変数たち

コードの冒頭にパラメータとなる変数たちが色々定義されている。

最初にparamで指定されているのが以下

• TR: 幅
• WRR: 幅のランダムさ
• DR: 密度
• LR: 長さのランダムさ
• ORIGIN: 中心

TRという名前は意味がわからないな。triangleの幅だろうが。 密度はどうしているかを見る。

let N_MAX = 400
# Number of lines. Interval is 2PI/N
let N = f32(N_MAX)*DR
let I = 2.0*PI/N

最大で400本として、それをDRで割り引く感じか。 Iは一区画あたりの角度だな。

# Shorter edge of canvas (width or height).
let SIDE = f32(min(*input_u8.extent()))

# Start line from about half of shorter edge.
let OFFSET = SIDE/4.0

SIDEはキャンバスの縦と横のうち短い方。

OFFSETは不思議な数字だな。あとのコードをざっと確認すると中心から直線の始まりがどれくらい離れているか、を表してそう。

でもこれがSIDEの半分の半分というのは結構広い気がするな。 ランダムを足すので意外と近くまで行くという事っぽいが。 この値も多分パラメータにする方が良さそうではある。

とりあえず最初に定義される変数は大体わかったので次に行こう。

主要な点と角度たち

最初はコードをロジックと対応づけて解説していこうと思ったのだが、 思ったよりも大変になりそうな上にコード読む方が早い、となりそうだったので、 予定を変更してここではコードを読む事を前提に、その助けになりそうな変数の説明をする事にする。

コードを読む上でややこしいのは点や角度が何を表しているか、だと思うので、 主要なものを図示しておく。

まずは区画関連。 中心から、角度Iごとに区画に分けてある。

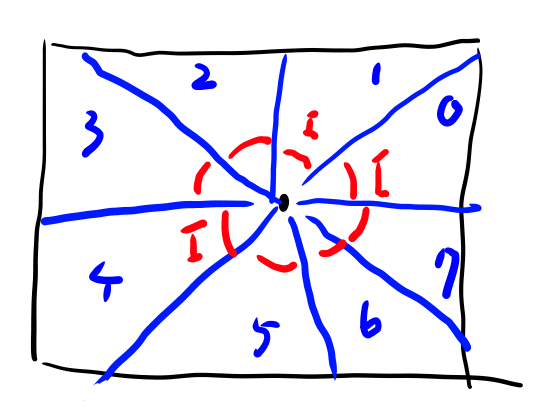
各区画のインデックス（青で0, 1, 2と書いてあるもの）を、コードではAと呼んでいる。 基本的には現在対象としている点がどの区画に属しているかを計算したら、 以後はその区画内の事だけを考えれば良い。

次に区画内の主要な変数は以下。

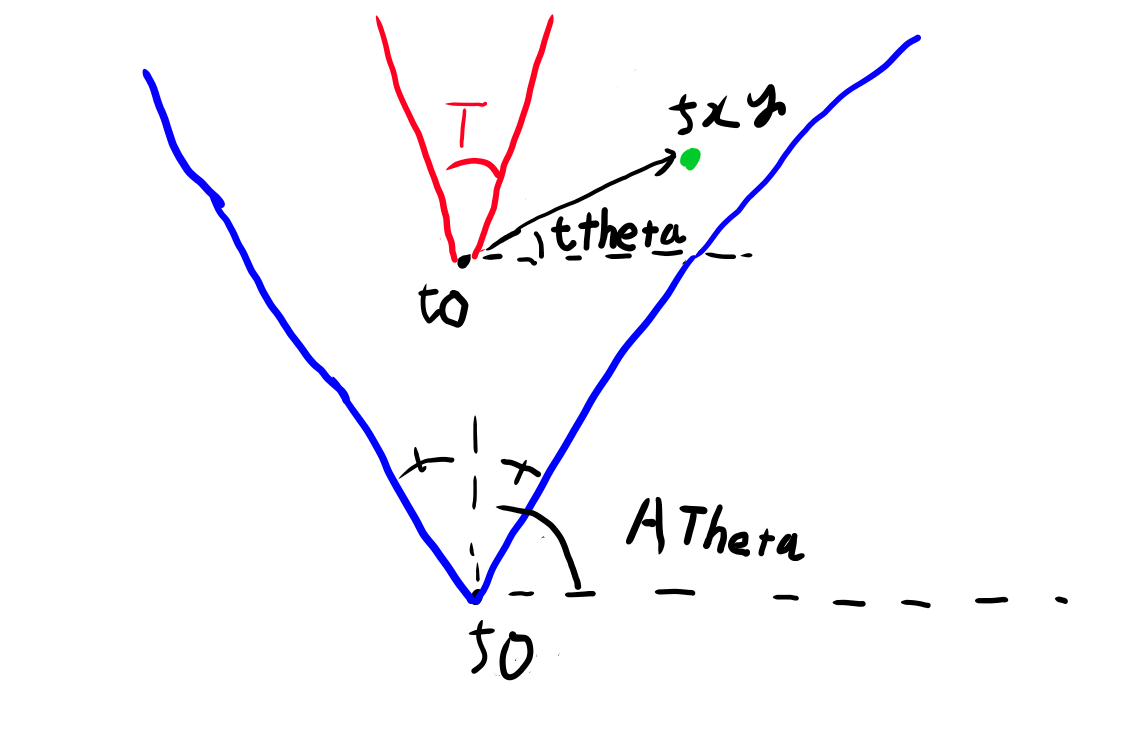
AThetaは区画の真ん中を通る線のなす角。

以上の変数を元に、ロジックの中心となる三角形の中にあるかどうかを判定する部分を見ていこう。

三角形の中かどうか

先ほどの図は偶然真上っぽくなっていて誤解を招くので、少し傾けた図で考える。

真ん中はAThetaで、内側の方の赤い線はこれに0.5Tを引いたものになっていそう。

すると、前の図のtthetaが、ATheta-0.5*T以上、Atheta+0.5*T以下なら三角形の中っぽい。

つまり引いた絶対値が0.5*Tの範囲なら良さそう。

コードとしては以下の部分か。

     ifel(abs(ttheta-ATheta) < T/2.0, 1.0, 0.0)

まとめ

• 集中線は区画に分けて、区画の中に三角形を描く事で実現出来ているよ
• GPU的に書く必要があるので、与えられた点から考える必要があるよ

追記: アンチエイリアスの改善を行いました

先っぽの品質が気になったので、より真面目なアンチエイリアスの実装を以下で行いました。

MFG： 集中線のアンチエイリアス改善