MFG： 集中線のアンチエイリアス改善

MFG： 集中線の解説で作ったフィルタは、先っぽのアンチエイリアスの効きがいまいちだ。

これを改善していきたい。 なお、アンチエイリアスはここでは略してAAと呼ぶ事にします。アスキーアートではありません。

アンチエイリアスの解説は、須崎さんの「2Dグラフィックスの仕組み」が平易でありながら詳しく書かれているのでおすすめです。

amazon: 2Dグラフィックスの仕組み

この本はCPUを前提に書かれているのでGPUプログラミングが基本となるMFGとは違う部分もありますが、 GPUプログラミングで画像処理をするにしても、必要となるグラフィックス処理の知識はどこかで学ぶ必要はあります。 この本はアルゴリズムの解説だけでなく、それらの前提となるピクセルの解釈や理論的にはスッキリしないが実際の応用に必要な事なども全て網羅されているので、 この本とGPUプログラミングの本を併用するのがオススメです。

以下の解説でもこの書籍の関連するページも示しておきます。全体的にはp95の2.06にある、斜めの直線の描画からの話となります。

現状のサブピクセル（スーパーサンプリング）のAA

エイリアスが何故起こるのかの問題と対策を考える前に、現状は何をやっているのかの説明を簡単にしておきます。

現状は3x3のサブピクセルによるアンチエイリアスを行っています。 これは対象とする点に対して、ピクセルのサイズの1/3の仮想的なピクセルがあるとして、この3x3のピクセルの計算を行った後に、 その寄与度を足して9で割る事で半透明にする、というものです。

これは実装が簡単な割に効果も高いので、試作の段階ではとりあえず採用している事が多く、集中線でもそうでした。

「2Dグラフィックスの仕組み」ではp106の円のアンチエイリアスのあたりに解説があります。

実装例

該当するのは以下の部分です。

  @bounds(3, 3)
  def occupy |xi, yi| {
    let fxy = fxy0 - [0.33, 0.33] + 0.33*f32[xi, yi]
    ...
    ifel(abs(ttheta-ATheta) < T/2.0, 1.0, 0.0)
 }

  let avg_occupy = rsum(0..<3, 0..<3) |rx, ry| { occupy(rx, ry) }/9.0

ですが、昔に書いたコードなので何故かローカルテンソルを使っています。 多分当初は集中線をどう実現するのか良くわからず、試行錯誤した結果こうなっているのだと思います。

普通はrsumで以下のようにします。

  let avg_sum = rsum(0..<3, 0..<3) |xi, yi| {
    let fxy = fxy0 - [0.33, 0.33] + 0.33*f32[xi, yi]
    ...
    ifel(abs(ttheta-ATheta) < T/2.0, 1.0, 0.0)
  }
  let avg_occupy = avg_sum/9.0

自分のフィルタにサブピクセルAAを追加しようと思う場合はこちらのコードを使うと良いでしょう。

コードを見ると、縦と横に対して、-0.33, 0, +0.33だけずらした点をピクセルと見て計算をして、それぞれに1.0か0.0を返しています。 1.0が黒を打つ、0.0が透明です。そしてこの結果を3x3で足した結果のavg_sumを、最後に9.0で割って平均を取っています。

ほとんどのアルゴリズムでxとyについて計算している所をこのrsumで覆って最後に9.0で割るだけで実装出来るので、他のアルゴリズムにも簡単に流用出来ます。

サブピクセルAAの利点と欠点

サブピクセルによるアンチエイリアスのメリットとデメリットを簡単に示しておきます

利点

• 実装が簡単：ロジックに一切手を入れずに実装出来る
• アルゴリズムに依らない: どんなアルゴリズムでも同じ実装で良いので、問題ごとにアンチエイリアスを考える必要が無い
• 異常値が出ない: 角度が0度の付近であれ、垂直付近であれ、安定した結果が得られる

欠点

• 本質的な解決では無いため、必ず元と同じエイリアスが発生する（ただし程度は弱まる）
• アルゴリズムによっては計算量が大きい
  • 元のアルゴリズムを単純にサブピクセルの数だけ繰り返すので、元のアルゴリズムが重いと計算コストが高い

サブピクセルは結局はピクセルの幅を考慮に入れていない、という事実は変わらないので、 エイリアスの議論をする時にはAA無しと全く同じ事情となります。

結果の評価

サブピクセルのAAの効果を実際に見てみましょう。

アンチエイリアス無し

先端が途切れて点線になったり、斜めがカクカクしたりしてます。これは酷いですね。

次にサブピクセルによるAA

比べてみると圧倒的に綺麗になりますね。冒頭の大きく拡大した絵では随分汚く見えますが、普通のサイズではこれでも実はかなり綺麗です。 ただし大きく拡大すると上と同じような現象は確認できます。

サブピクセルAAは、この簡単さでこの綺麗さなので、とりあえず試してみて、これで満足してしまう事も少なくありません。

集中線におけるエイリアスのメカニズム

集中線の正しいアンチエイリアスについて考えてみます。 そのためには集中線ではなぜエイリアスが起きているのかを理解する必要があります。

理論的にはなぜエイリアスが起きているのかと、数学的にはどうしなくてはいけないのかはほぼ同じ話でもあります。

ピクセルの位置と幅

まず、エイリアスを真面目に考える場合、ピクセルの座標がどこを表しているのか、というのはちゃんと考える必要があります。 理論的には座標はピクセルの中心となります（左上ではありません）。 詳細は「2Dグラフィックスの仕組み」のp96あたりに解説があります。

そして多くのアルゴリズムで、このピクセルの中心の位置がある境界の内側か外側かで0か1かを決めるのが点を打つ基本となります。

解像度が無限であれば、これで厳密に正しい結果となります。

ですが実際にはピクセルには幅と高さがあります。そこで、境界に部分的にまたがるようなピクセルも出てきてしまいます。 このまたがっているピクセルを、境界の中にある割合をアルファ値とする事が厳密なアンチエイリアスとなります。

厳密解や、それの多少の近似をしたほぼ厳密な解は、境界となる線の数学的な表現に依存するので、 アルゴリズムごとに専用の処理を考える必要があります。

三角形にまたがるケース

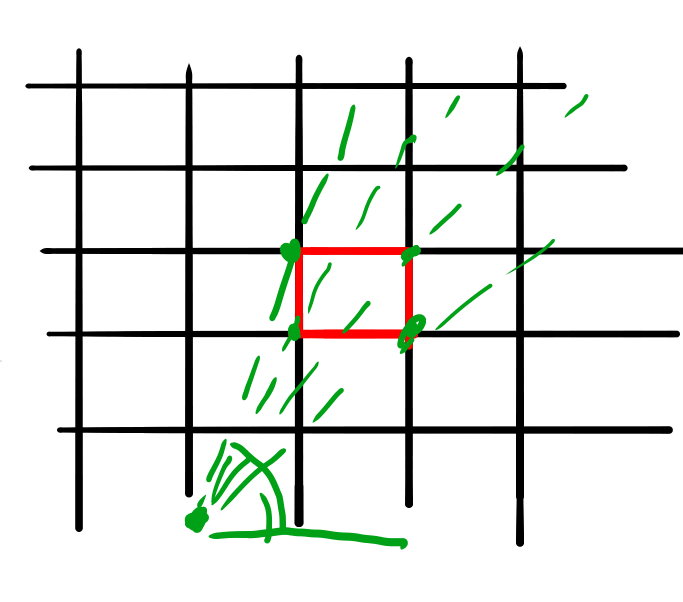
集中線の場合は、MFG： 集中線の解説の「主要な点と角度たち」で書いた図が関連する所になります。 図を再掲しておきます。

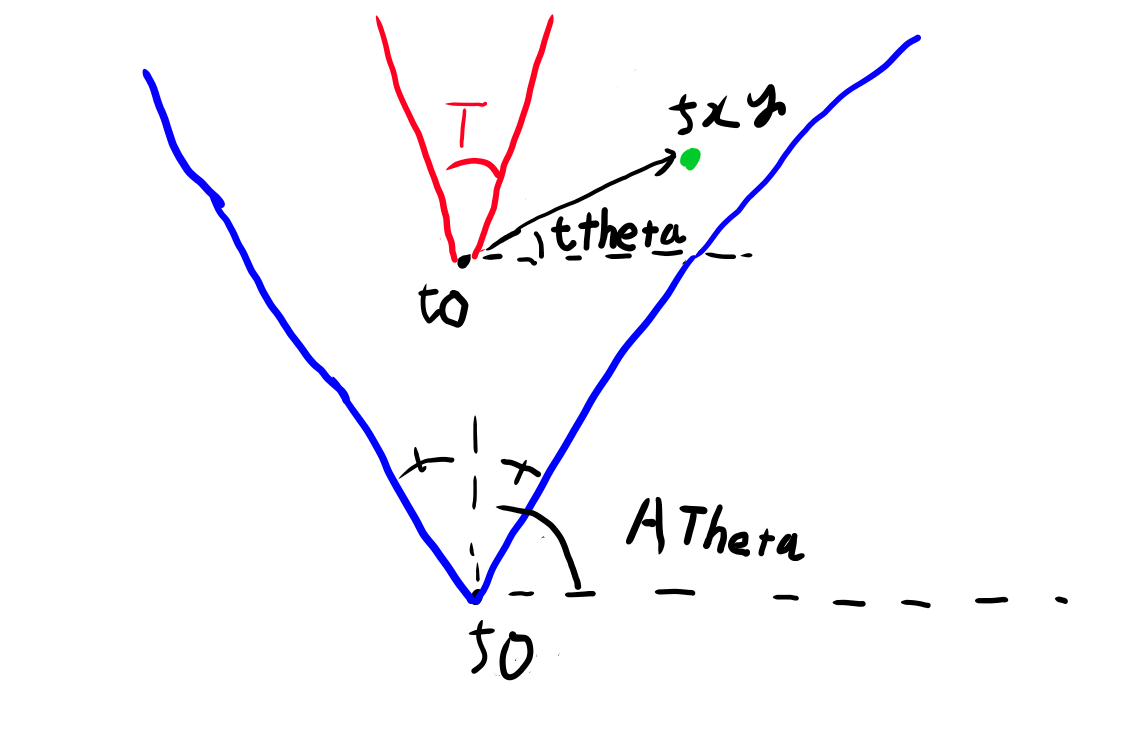
この図で、赤の線と緑の線の関係が基本となります。 それは角度だけ見れば良くて、ATheta - T/2の線（赤の線）とtthetaの大小関係が、境界の中か外かを判定する基準となっていました。

ですがピクセルに幅と高さがある事を考えると、緑のベクトルは本当は線では無く、こちらも三角形となります。

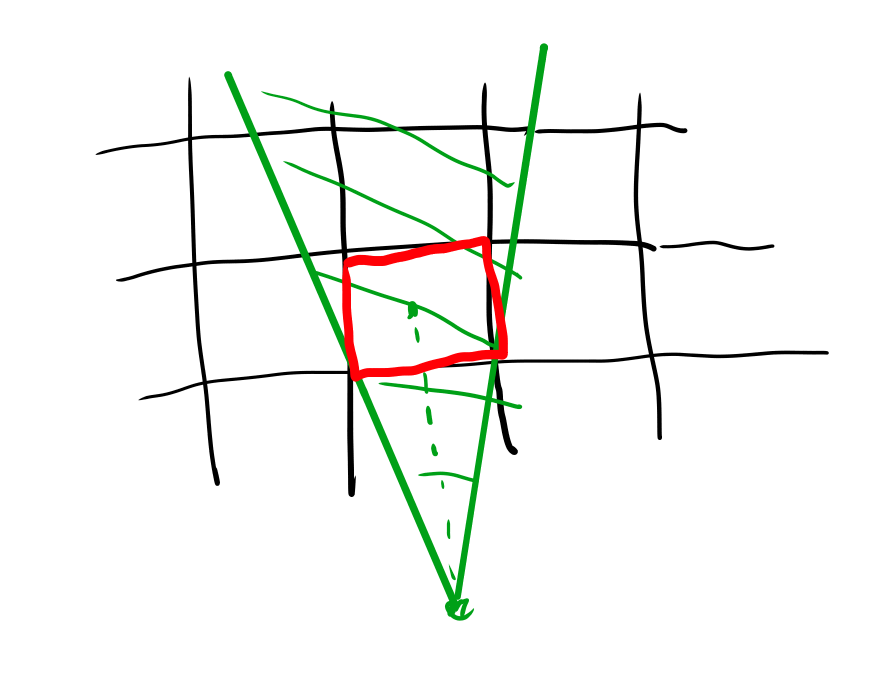
上の図で、赤い四角のピクセルを考える時に、幅を考えていない時は緑の点線がx軸となす角度を考えれば良いのですが、 幅を考えると緑の三角形の範囲の角度を考える必要がある、という事です。

この緑の三角形と赤の三角形のオーバーラップ具合でアンチエイリアスを考える必要があります。 厳密にはオーバーラップしている範囲のピクセルの長方形の面積の割合になりますが、 大雑把にはオーバーラップしている角度の割合でいいでしょう。

オーバーラップする様々なケースを考える

ざっと考えると以下のような場合がありそうです。

• 完全に外
• 完全に中
• 部分的に外
  • 赤がピクセル幅より大きい場合
  • 赤がピクセル幅より小さい場合

完全に外

完全に中

部分的に外、赤の方が大きいケース

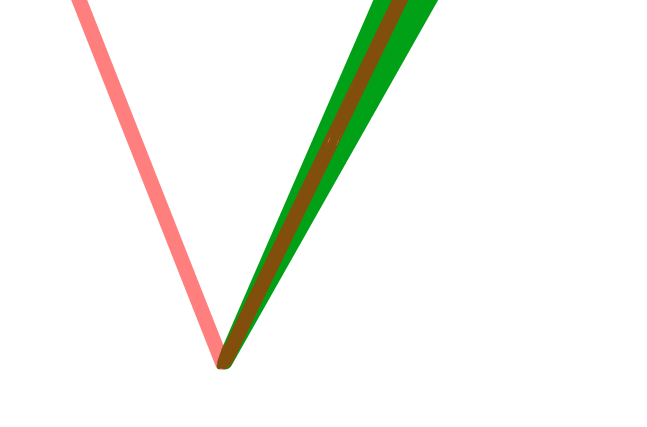
部分的に外、両方はみ出るケース

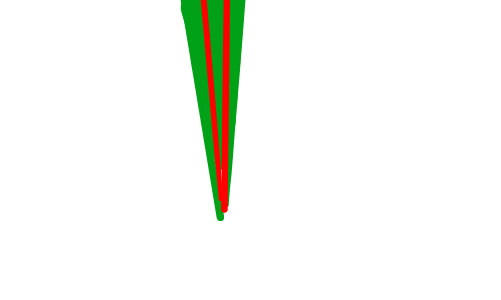
描いてみて気づきましたが、最後は片方だけはみ出るケースは一つ上と同じことになりそうなので、赤の方が大きいかどうかよりも、本質的には両方にはみ出ているかどうか、 と考える方が正しそうですね。

右にはみ出ている割合と左にはみ出ている割合を計算してそれを引いてやれば、全ての場合を統一的に扱えそうです。

アンチエイリアスの具体的な計算

理論的にはピクセルのオーバーラップの割合は、tthetaの周りの緑の三角形とAThetaの前後T/2の範囲のオーバーラップ具合の割合で良さそうでした。

赤の範囲は厳密に計算出来ているので、あとは緑の範囲を求めて、そのオーバーラップを計算すれば良さそうです。

緑の幅の計算方法

緑の幅は、何も考えないと角度によって場合分けが必要ですが、少し考えてみると、 ピクセルの4頂点で角度を出して、その最大値と最小値で良さそうです。不要な点が二つ入りますが、最大と最小で必ず消えるので問題ないでしょう。

ただ、0と2パイの境界の所では不連続になるので当別扱いが必要そう。 とりあえず特別扱いはせずに処理をして、他が動いていたら最後に直す事にして、ここではその特別扱いは考えない事にしましょう。

4頂点というのは、ピクセルの幅と高さの1/2を引いたり足したりする事で得られます。 ピクセルの幅が1、高さが1と思っているので、半分は0.5なので、以下の4点を考えれば良い、という事でしょうか。

(x-0.5, y-0.5)
(x+0.5, y-0.5)
(x-0.5, y+0.5)
(x+0.5, y+0.5)

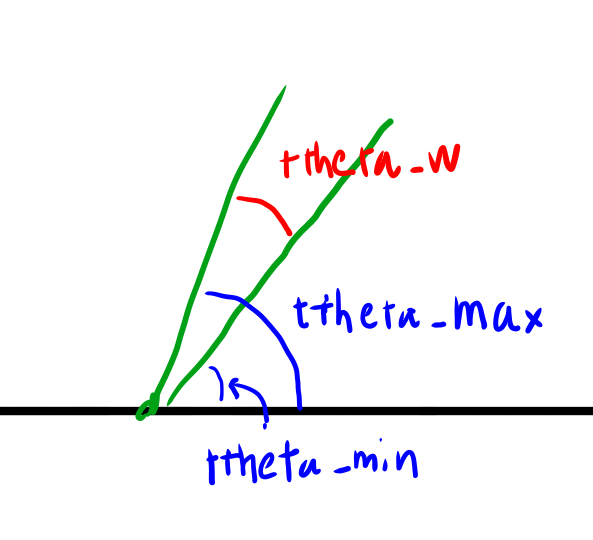
以下図で、赤のピクセルが締める範囲の角度の最大値と最小値が、少なくとも4点計算した最大と最小値がそれになっている、というのは分かるでしょう。 真ん中の2本は無駄なので計算する必要は無いはずですが、最大値と最小値には影響は無いはずです。

これで得られた最小値と最大値をttheta_min、ttheta_max、そしてその差分をttheta_wと呼ぶことにしましょう。

コードとしてはreduceを使えば計算出来そうです。

# toまでは前回のコードと同じ

let AT_min = ATheta-T/2.0
let AT_max = ATheta+T/2.0

let [tt_min, tt_max] = reduce(init=[-1.0, -1.0], 0..<2, 0..<2) |i, j, accm| {
    # (x-0.5, y-0.5), (x+0.5, y-0.5), (x-0.5, y+0.5), (x+0.5, y+0.5)
    let fxy = fxy0 -[0.5, 0.5] + f32[i, j]   
    let theta = atan2xy(*(fxy-to))


    ifel( accm < -0.5, vec2(theta), [min(accm.x, theta), max(accm.y, theta)])
}

accmの不等号の-0.5には深い意味は無いけど0よりも小さいが精度で0を拾ってしまわないように少し余裕を持って小さめな数字。

右にはみ出ている割合

右にはみ出ている割合と左にはみ出ている割合を計算して引けばオーバーラップしている割合が残りそうです。 そして右が出来れば左は同じ計算と思うので、右の計算だけを考えましょう。

右の線はATheta-T/2なので、これとttheta_maxやttheta_minの大小関係に応じて割合が決まるか

• ttheta_maxの方が小さい: ttheta_w
• ttheta_minの方が大きい: 0
• その間: 求めたい値

間のケースを考える。 はみ出ている割合はATheta-T/2 - ttheta_minか。

つまり、以下でいいのかしら？

clamp(ATheta-T/2.0-ttheta_min, 0, ttheta_w)

よさそうな気がする。

実装してみる

以上を踏まえて、角度のオーバーラップの割合をアルファとするアンチエイリアスを実装してみた。

概ね以下のようになる。

  let tt_w = tt_max - tt_min

  let r_over = clamp(AT_min-tt_min, 0.0, tt_w)
  let l_over = clamp(tt_max - AT_max, 0.0, tt_w)

  let overwrap = tt_w - r_over - l_over
  let avg_occupy = overwrap / tt_w  

この結果は以下。

とても綺麗になりました。サブピクセルAAで見られた最後が点線になってしまう現象も無くなっています。

水平の0を跨ぐ所の処理

現状は最大値と最小値という所でマイナスになったり2パイから0になる所の処理を何もしてないので、変になっているはず。

実際に見てみると以下のように、水平の所に空白が出来ていた。

この0の付近では2パイになったり0になったり不連続に変化しているが、そういう区画はたかだか一つしか無いはずで、 その区画内では全ての角度に2パイを足した数値で統一すれば連続になると思われる。

区画を計算する基準となる角度が、ギリギリ2パイになる時とギリギリ0以上になる時の両方を考慮に入れると、 区画の片方がマイナスになるときと2パイより大きくなる時の両方でこの補正を入れれば良い。

補正前に0のsuffixをつけて計算すると、以下のような感じか。

  let tt_center_0 = atan2xy( *(fxy0-fo) )
  let A0 = round(tt_center_0/I)
  let ATheta0 = A0*I

  let offset = ifel(ATheta0-I/2.0 < 0.0 || ATheta0+I/2.0 > 2.0*PI, 2*PI, 0.0)

このffsetは問題の区画以外ではいつも0.0となる。 そしてこれが0.0じゃない区画では、2パイ側では何もせず、0より上側では2パイを足せば良い。

fn continuise |offset: f32, rad: f32| {
  ifel(rad > PI, rad, rad+offset)
}

ifelのPIは2PIのそばという条件なのだけれど、offsetが0.0でなければradがある程度大きければ十分なのでPIとした。 なお、引数の順番はパイプラインで使うためにこの順番になっている。

これで以下のように、水平線の空白が消えた。

全体のコード

最後に全体のコードを載せておく。

@title "集中線"

# Specify width by ratio of I.
@param_f32 TR(SLIDER, label="幅",  init=0.5, min=0.1, max=1.0)
@param_f32 WRR(SLIDER, label="幅ランダム",  init=0.2, min=0.0, max=1.0)
@param_f32 DR(SLIDER, label="密度", init=0.5, min=0.01, max=1.0)
@param_f32 LR(SLIDER, label="長さランダム",  init=0.2, min=0.0, max=1.0)
@param_pos ORIGIN(POINTER, label="中心")

let PI = 3.141592
let N_MAX = 400
# Number of lines. Interval is 2PI/N
let N = f32(N_MAX)*DR
let I = 2.0*PI/N


# Shorter edge of canvas (width or height).
let SIDE = f32(min(*input_u8.extent()))

# Start line from about half of shorter edge.
let OFFSET = SIDE/8.0

# N random number, but N is not known  in advance, so create N_MAX.
@bounds(N_MAX, 2)
def RAND_TABLE |x, y| { rand() }

# return positive region theta. arg order is x, y for spread usage
fn atan2xy |x: f32, y: f32| {
  let theta = atan2(y, x)
  ifel(theta > 0.0, theta, 2.0*PI+theta)
}

# Adding offset if rad is near 0.0.
# offset is either 0.0 or 2.0*PI.
# This make "2*PI-eps" to "eps" to be "2*PI-eps" to "2*PI + eps", which is continous.
# offset is first for better pipelining.
fn continuise |  offset: f32, rad: f32 | {
  ifel(rad > PI, rad, rad+offset)
}

def result_u8 |x_0, y_0| {
  # ORIGIN to pixel pos.
  let fo = ORIGIN*f32(input_u8.extent())

  let fxy0 = f32[x_0, y_0]

  let tt_center_0 = atan2xy( *(fxy0-fo) )
  let A0 = round(tt_center_0/I)
  let ATheta0 = A0*I

  let offset = ifel(ATheta0-I/2.0 < 0.0 || ATheta0+I/2.0 > 2.0*PI, 2*PI, 0.0)
  let tt_center = continuise(offset, tt_center_0)

  # Index of I.
  let A = round(tt_center/I)
  # Basic angle of this pos.
  let ATheta = A*I
  let AI = i32(A)

  # Width of line, stands for the angle of triangle. Randomness is added for each A.
  let T = TR*(1.0-WRR*RAND_TABLE(AI, 0))*I

  # Length of origin. Away from OFFSET+random.
  let RO = OFFSET*(1.0+2.0*LR*RAND_TABLE(AI, 1))

  # to: Origin of triangle
  let to =  fo + RO* [cos(ATheta), sin(ATheta)]

  let AT_min = ATheta-T/2.0 |> continuise(offset, ...)
  let AT_max = ATheta+T/2.0 |> continuise(offset, ...)

  let [tt_min, tt_max] = reduce(init=[-1.0, -1.0], 0..<2, 0..<2) |i, j, accm| {
    # (x-0.5, y-0.5), (x+0.5, y-0.5), (x-0.5, y+0.5), (x+0.5, y+0.5)
    let fxy = fxy0 -[0.5, 0.5] + f32[i, j]   
    let theta = atan2xy(*(fxy-to)) |> continuise(offset, ...)


    ifel( accm < -0.5, vec2(theta), [min(accm.x, theta), max(accm.y, theta)])
  }

  let tt_w = tt_max - tt_min

  let r_over = clamp(AT_min-tt_min, 0.0, tt_w)
  let l_over = clamp(tt_max - AT_max, 0.0, tt_w)

  let overwrap = tt_w - r_over - l_over
  let avg_occupy = overwrap / tt_w  

  u8[0x0, 0x0, 0x0, round(255.0*avg_occupy)]
}

雑感

真面目に実装したアンチエイリアスのコードとスーパーサンプリングによるアンチエイリアスのコードを比較すると、 行数としては真面目に実装したアンチエイリアスの方がむしろ短くなっていて、計算コストも低くなっています。 結果も拡大すれば明らかに違いが分かるくらいクオリティには差が出ます。

一方、真面目に実装したアンチエイリアスは問題ごとに実装する必要があり、正しく動いているかもいちいち問題ごとに検証する必要があります。 スーパーサンプリングのAAはどこかで動く実装があれば、それを持ってくるだけでほぼ正しい事が保証されるので、 問題ごとに開発するコストはありません。 スーパーサンプリングのAAはコード量はそれなりになりますが、どこかで実装したものを持ってくるのは簡単です。

クオリティに関して。両者のAAは、拡大すると凄く違います。両者の結果は明らかに優劣がある。 けれど、普通のサイズではかなり微妙な違いで、ここで見るほど明らかな違いではありません。

それらの微妙な差異と比べると、アンチエイリアスがあるか無いかの差は拡大しなくても明らかに分かる大きな違いとなります。 この手の処理でアンチエイリアスをしない、というのは選択肢にはならないでしょう。

こうした違いは、実際に手元で確認しながら考えてみるのが面白いと思います。 こういう実験が簡単に出来るのは、MFGStudioの良い所ですね。