MFGで基本図形を描いてみよう（後編）

MFGで基本図形を描いてみようシリーズの後編です。
前編はこちら＞MFGで基本図形を描いてみよう（前編）

今回の記事もMFG Studioで開発、動作確認しています。

前編では縦の直線と円を描き、サブピクセルによるアンチエイリアスを実装したりもしました。 後編では斜めの線と三角形を描いてみます。

斜めの線を描こう

斜めの線を描きます。x1, y1からx2, y2までの線を描きます。

数学的に正しいやり方はx, yからこの直線までの距離を求めて、その範囲が一定以内なら点を打つ、みたいな事をやるのですが、 ちょっと面倒なので幅の値は手抜きして、あるxについて、以下のような順序で考える事にしてみましょう。

1. xがx1とx2の間でなければ透明
2. xがx1とx2の間の時、その点の直線上のyの値を求める
3. 現在のyがその求めたyのそばだったら点を打つ

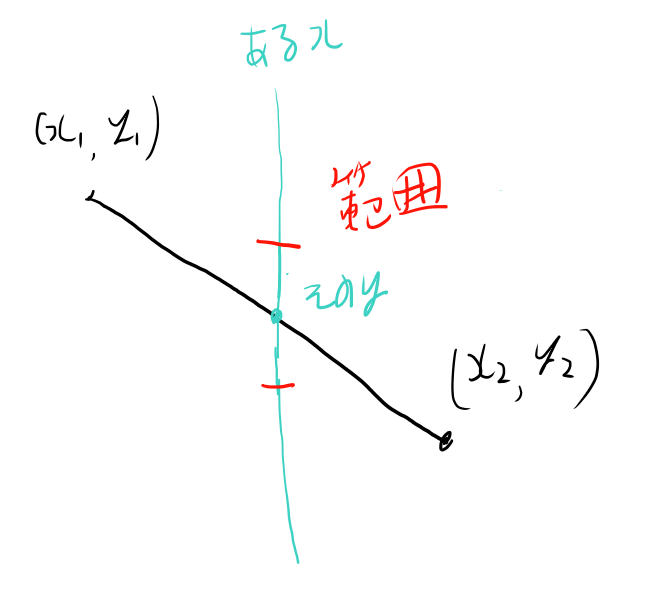
x1, y1とx2, y2は適当にハードコードして、以下にしましょうか。

let v1 = [0.2, 0.3]
let v2 = [0.5, 0.7]

まずはこの点を打ってみましょう。このv1かv2の近くだったら、つまりdistanceが小さかったらfgcolを描くようにしましょう。

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])
  ifel(distance(v1, fxy) < 0.01 || distance(v2, fxy) < 0.01, 
        fgcol, bgcol) \
  |> to_u8color(...)
}

パイプ演算子を使う時に前の行の最後をバックスラッシュでエスケープするのはたまにやる書き方です。

つぎに直線の方程式に代入してこのxでの直線上のyの値、y3を求めます。

雑に計算をして

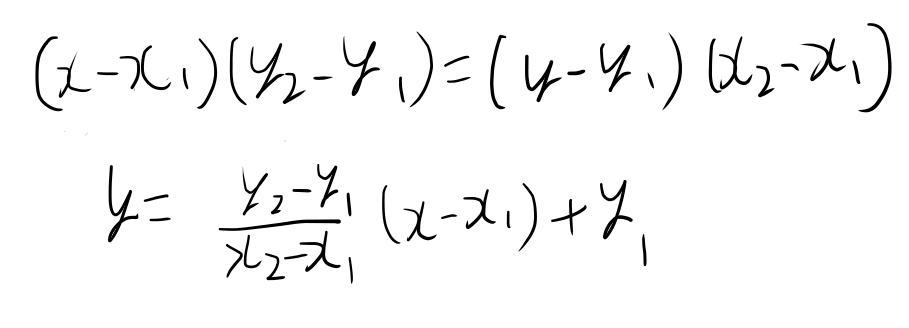
  let y3 = (v2.y - v1.y)/(v2.x-v1.x)*(fxy.x-v1.x) + v1.y

となるので、全体としては以下のようなコードになりそうです。

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])
  let y3 = (v2.y - v1.y)/(v2.x-v1.x)*(fxy.x-v1.x) + v1.y

  let xinside = (fxy.x >= v1.x) && (fxy.x <= v2.x)
  let yinside = abs(y3-fxy.y) < 0.01

  ifel(xinside && yinside, fgcol, bgcol) \
  |> to_u8color(...)
}

ちゃんと描けてそうです。

直線もキレイに描く

拡大してみると斜めの線はガタガタです。

という事でアンチエイリアスを考えてみましょう。 前回同様、部分的に直線の範囲に入っているピクセルはアルファを調整する事で滑らかになるはずです。

カバー率を直接求める事も出来そうですが、今回も何も考えずにサブピクセルで被覆率を求める方針にしましょう。

let divNum = 4

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])
  let fwh = input_u8.extent() |> f32(...)
  let eps = 1.0/(fwh*divNum) # 1ピクセルあたりの差分を4分割
  let cover = rsum(0..<divNum, 0..<divNum) |rx, ry| {
    let fxy2 = fxy + f32[rx, ry]*eps
    let y3 = (v2.y - v1.y)/(v2.x-v1.x)*(fxy2.x-v1.x) + v1.y

    let xinside = (fxy2.x >= v1.x) && (fxy2.x <= v2.x)
    let yinside = abs(y3-fxy2.y) < 0.01
    ifel(xinside && yinside, 1.0, 0.0)
   }
   let ratio = cover/(divNum^2)
  [*fgcol.xyz, ratio*fgcol.w] |> to_u8color(...)
}

このコードをぱっと見せられて解読するのは大変ですが、fxy2についてこれまでの処理をして、入っていたら1.0, 外れていたら0.0にしてその個数を数えて割合にする、 という流れに注意すると割と一つ前のコードと大差ない事に気づきます。

きれいな線になりました。拡大していると少しガタガタして見えますが、もう少しふつうの拡大率で見るとキレイに見えるのが分かって満足度が高いです。

追記: やはり垂線の距離をちゃんと求めてみる

ブログをnattou.org先生に見てもらった所「斜めの線をちゃんと垂線の距離を出さないのはいかがなものか？」と言われて泣きながら計算することにしました。

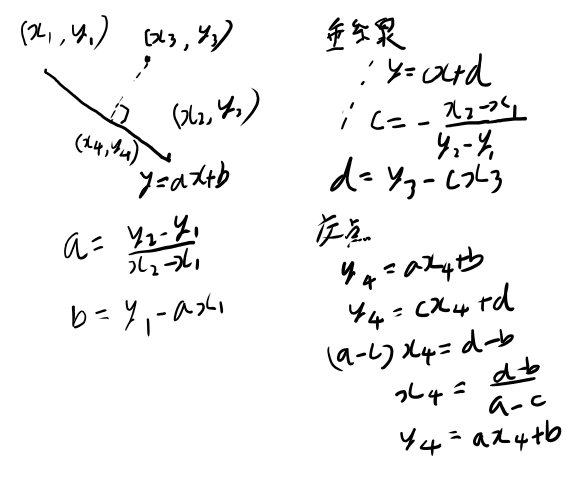
プログラムとしては、既に定数が計算されたらその定数は既知として進めれば良いので、全部手計算するよりは楽です。 上の計算で言えばbの式ではaを使って良くてdの式ではcを使って良いという意味ですね。

こうして出したx4, y4とx3, y3の距離を出して、それが幅以下なら〜というアルゴリズムに変更してみましょう。

let width=0.01

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])

  # y = ax+bをまず出す。
  let a = (v2.y-v1.y)/(v2.x - v1.x)
  let b = v1.y - a*v1.x

  # 垂線、y=cx+dを出す
  let c = -1.0/a
  let d = fxy.y - c*fxy.x

  # 交点, x4, y4を出す
  let x4 = (d-b)/(a-c)
  let y4 = a*x4+b

  # x4, y4とfxyの距離を出す
  let dist = distance(fxy, [x4, y4])

  # 交点のx4が直線内かをチェックする。
  let xinside = (v1.x <= x4) && (x4 <= v2.x)

  ifel(xinside && dist <width , fgcol, bgcol) \
  |> to_u8color(...)
}

これで完璧、と思いきや、以下のようになってしまいました。

端が垂直になってません。これは縦と横が1:1じゃないためと思われます（円が歪むのと同じ理屈）。

その分を補正してみましょう。1.0 : 1.0では無く、横を1.0, 縦をaspect比を固定した座標系で全部計算することにし、 この座標系の点を最初にAをつけて区別しましょう。

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])

  let fwh = input_u8.extent() |> f32(...)
  let ratioY = fwh.y/fwh.x
  let Aratio = [1.0, ratioY]

  # A座標にする
  let Afxy = Aratio*fxy
  let Av1 = Aratio*v1
  let Av2 = Aratio*v2

  # 以下はAをつけるだけでロジックは一緒だが一応載せておく

  # y = ax+bをまず出す。
  let a = (Av2.y-Av1.y)/(Av2.x - Av1.x)
  let b = Av1.y - a*Av1.x

  # 垂線、y=cx+dを出す
  let c = -1.0/a
  let d = Afxy.y - c*Afxy.x

  # 交点, x4, y4を出す
  let x4 = (d-b)/(a-c)
  let y4 = a*x4+b

  # x4, y4とfxyの距離を出す
  let dist = distance(Afxy, [x4, y4])

  # 交点のx4が直線内かをチェックする。
  let xinside = (Av1.x <= x4) && (x4 <= Av2.x)

  ifel(xinside && dist <width , fgcol, bgcol) \
  |> to_u8color(...)

}

するとこうなりました。

無事端が垂直になっています。

三角形を描く

基本図形といえば四角、丸、三角です。四角はやってないじゃん、という話はありますが、四角は簡単なのでいいでしょう。

三角形は数学的にはちょっと難しい。3点p1, p2, p3が与えられた時に、ある点vがこの三角形の中か外かをどう判定するのか？ という話になります。 「外積を使って全部同じ法線方向なら内側、でどうですか？」とさらっとわかるならすぐにプログラムに入って良いのですが、 今回の記事のモチベーションとしては、数学の知識をGPUプログラムに活かす例を提供したい、 というのがあるので、数学の話もちょっとはしておきます。 ただし本題では無いので、全くこの辺わからない、という人向けの説明では無くて、 「昔こういうのやったけどもう全然覚えてない」という人向けの説明となります。

外積と法線の向き

2つのベクトルの外積というのがあります。 外積は自分たちの頃は高校生では習わない事になっているけれど、大学への数学とかの参考書では割と出てきていて、 難関大理系を受ける人ならだいたい知っているかな、というくらいでした。 昨今はどうですかね？

外積とは、ベクトルA、Bから、新しいベクトルCを作る手続きです。 ベクトルCはAベクトルからBベクトルに向かって右ネジを回した時にネジが進む方向となります。 長さは今回は使わないので気にしない。

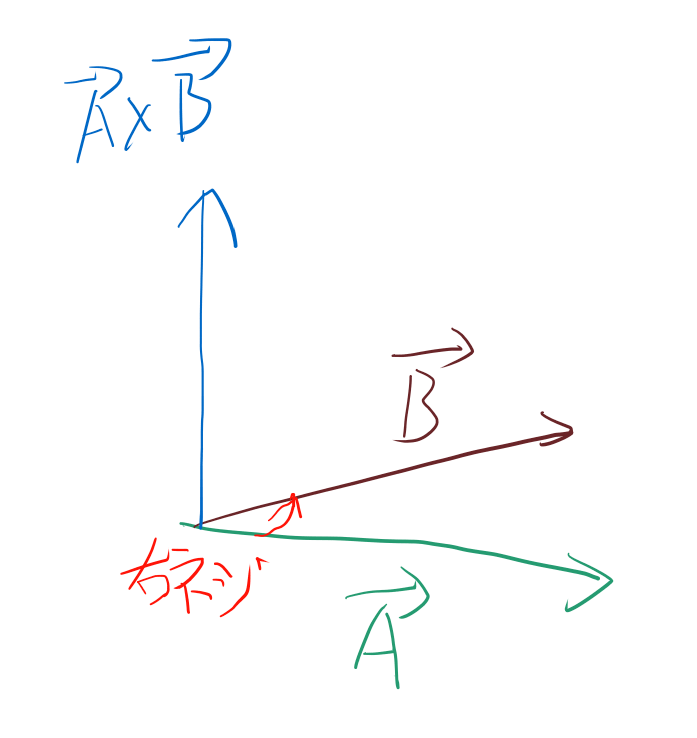
なお、xy平面上のベクトル2つの外積を取ると、それと垂直のz軸方向のベクトルとなります。

ある点vが三角形の中にあるか外にあるかを、この外積を使って求めるアイデアを感がてみます。

外積を使って点が三角形の中にあるか外にあるかを判定するアイデア

まずは数学的なことの前に、アイデアを漫画的に説明してみます。

三角形の各点に人を置いて、三角形を一周するような方向を向かせます（一周するならどちら向きでも良い）。

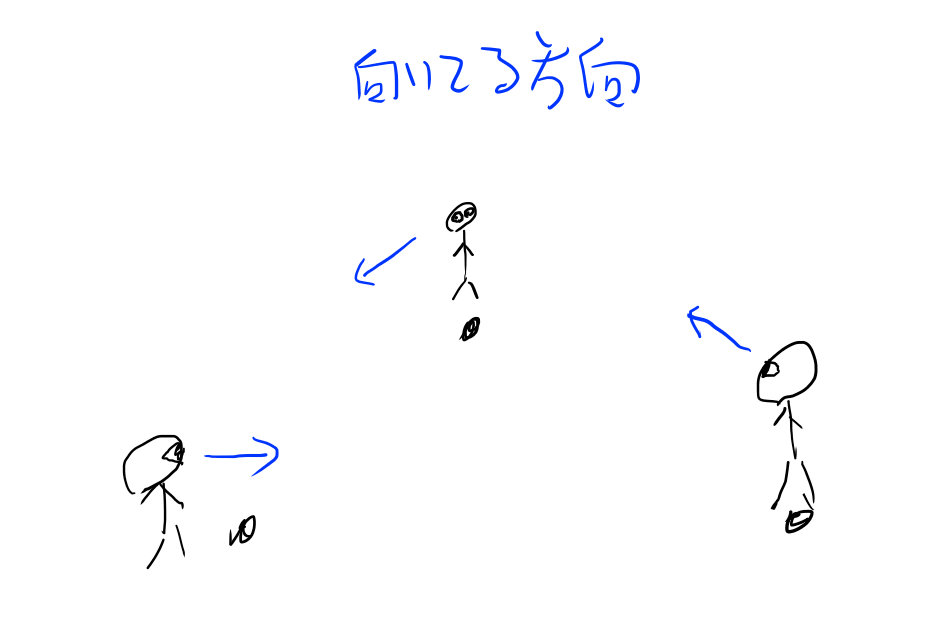
画力が微妙なのでわかりにくいですが、こんな感じです。

そしてそのそれぞれの人が、点vが左に見えるか右に見えるかを聞くのです。

点vが三角形の中の場合

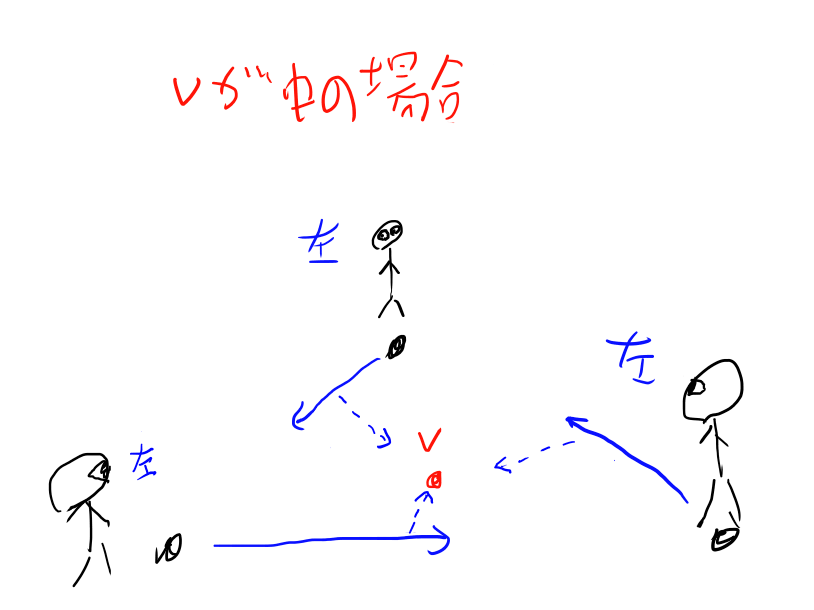
この図の点線（点vを向いている）が実線の右にあるか左にあるか、というのを各自に聞く訳ですね。

点vが三角形の中にある場合、全員が同じ方向を答えるはずです。左と言うか右というかは最初にどちら側を向いているかの問題になりますが、 とにかく全員にとって同じ側に見えるならそれは三角形の中、という意味になります。

点vが三角形の外の場合

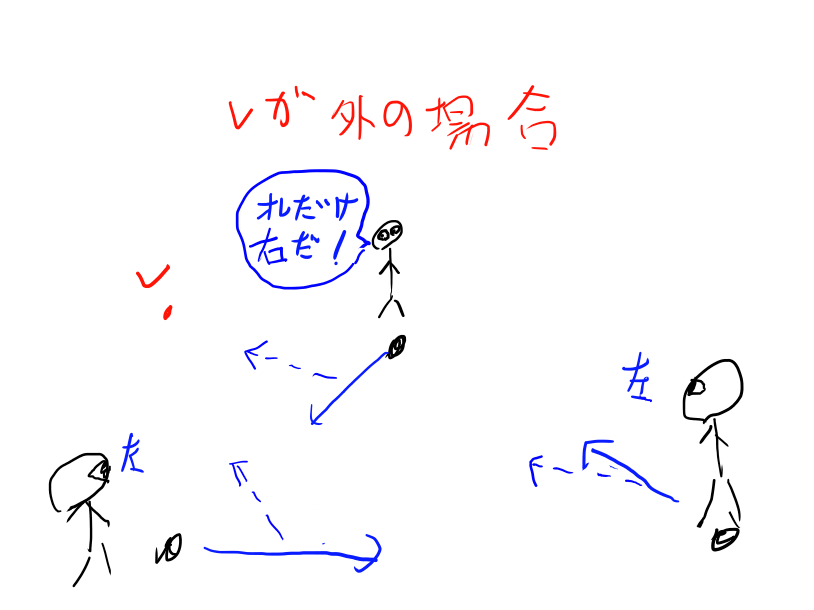
この場合、一人だけ違う向きを答えることになります。

ということで、点vが右と左のどちらに見えるかを全員に申告させて、それが同じ答えなら内部、違う答えの人がいれば外部、となります。

アイデアを外積を使って数学的に表現する

先ほどのアイデアを外積を使って表現してみましょう。 最終的には三角形の三点はp1, p2, p3と呼ぶ予定ですが、とりあえず今は説明のためA, B, Cと呼ぶことにします。

そしてABベクトル、BCベクトル、CAベクトルを考えます。

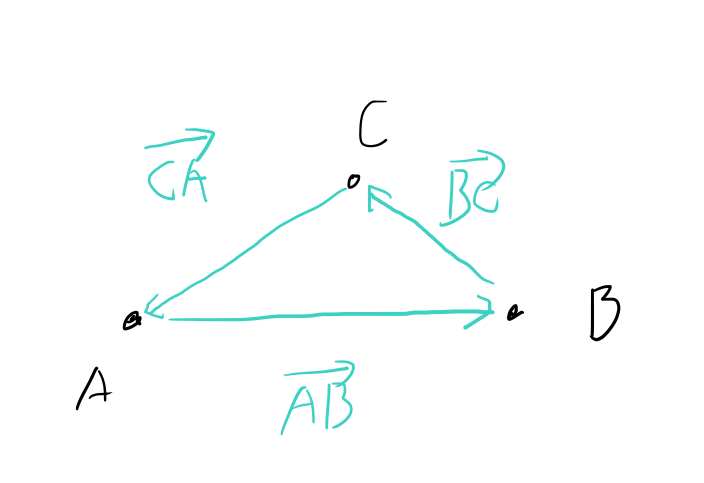
そしてある点vについて、A, B, Cのそれぞれの点からvへのベクトルを考えて、 それと先程の一周するベクトルの外積を計算していきます。

例えば頂点Aの例が以下になります。

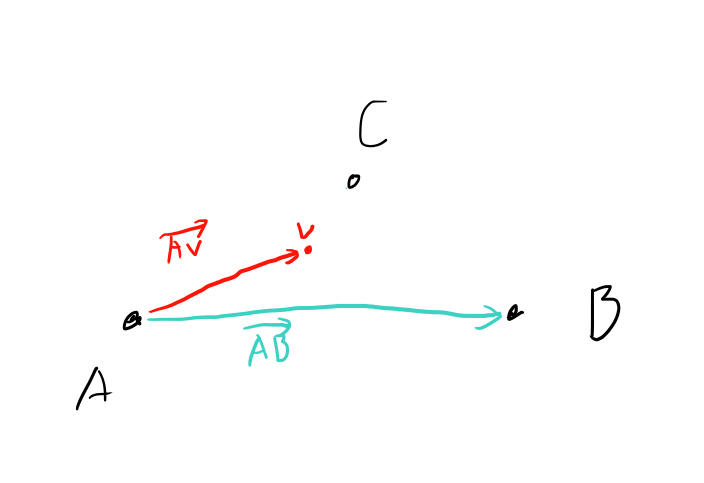
この2つのベクトルについて外積を取る。

これと同様のことをB, Cでもやっていき、外積の結果のz座標の符号を見ます。 全部同じ符号だったら三角形の中、違う符号があったら三角形の外、となります。

MFGで実装してみよう。

このアイデアで三点に囲まれた三角形を描いてみましょう。

外積は手で計算してもいいですが、MFGにはcrossという関数があります。

MFG/docs/ja/Reference/BuiltinFunctions.md at main · karino2/MFG

f32v3 cross(x:f32v3, y:f32v3)

xとyが3次元なのに注意してください。z軸には0.0を入れておけばOKです。

@title "三角形"

let fgcol = [0.0, 0.0, 1.0, 1.0]
let bgcol = [0.0, 0.0, 0.0, 0.0]

# 3次元でz軸は0.0にする
let p1 = [0.3, 0.2, 0.0]
let p2 = [0.4, 0.7, 0.0]
let p3 = [0.7, 0.4, 0.0]

def result_u8 |x, y| {
  let v = [*to_ncoord([x, y]), 0.0]
  let AB = p2-p1
  let BC = p3-p2
  let CA = p1-p3
  let Av = v-p1
  let Bv = v-p2
  let Cv = v-p3

  let z1 = cross(AB, Av).z
  let z2 = cross(BC, Bv).z
  let z3 = cross(CA, Cv).z
  let z = [z1, z2, z3]
  let inside = all(z > 0.0) || all(z < 0.0)
  ifel(inside, fgcol, bgcol) |> to_u8color(...)
}

無事三角形が描けました。

allなどを使うのはGPUプログラミングっぽいですね。

GPUで図形を描く問題について考える

三角形は割と難しい問題であり、CPUとの違いが大きい所でもあるので、ここで一歩引いてGPUでのグラフィックスプログラムの考え方について少し話しておきましょう。

三角形を描く、という時に、GPUでは全てのピクセルで外積を計算して正負をチェックして自分の点を打つかどうかを決めています。 これはピクセル一つ一つに人を置いて、それぞれの人に自身の点を打つかを計算させるようなことをしています。

それぞれの人が同じ計算を違うx, yについて行う。 これは非常にGPU的なやり方です。

CPUではこれはあまりにも無駄なのでもっと違う方法で描くでしょう。典型的にはy軸にそってスキャンライン的に左右の交点を求めて間を塗りつぶすのが普通のやり方と思います。

GPUのやり方はすごく無駄に見えますが、GPU的にはかなり負荷の少ない、早いプログラムです。 全てのピクセルでちょっとした計算をする、というのはすぐに終わる処理だ、という感覚を持つのはGPUプログラムにおいて重要です。

負荷とは別に、ここまでのプログラムはだいたい似た構造になっています。 それはxとyに対して、0か1かの計算をして1なら色を塗る、0なら塗らない、というような処理になっている所です。 これはある関数Fについて、以下の式を満たす領域を塗る、とも言えます。

\[F(x, y) > 0\]

このようなFを探すことがGPUで図形を描くことになります。 逆にこういうようなFが見つけられない図形を描くのは難しかったり、GPUでは不可能だったりします。

GPUプログラムはなんだか高校の数学の問題でエレガントな別解を探すような趣がある気がしています。

キレイな三角形にする

これはこれまでと同じなのでやらなくてもいいかな、とも思いますが、一応やっておきましょう。

拡大してみるとギザギザしています。

今回もサブピクセルにして前と同じことをしてみましょう。

let divNum = 4

def result_u8 |x, y| {
  let AB = p2-p1
  let BC = p3-p2
  let CA = p1-p3
  let v0 = to_ncoord([x, y])
  let fwh = input_u8.extent() |> f32(...)
  let eps = 1.0/(fwh*divNum) # 1ピクセルあたりの差分を4分割

  let cover = rsum(0..<divNum, 0..<divNum) |rx, ry| {
    let v1 = v0 + f32[rx, ry]*eps
    let v = [*v1, 0.0]
    let Av = v-p1
    let Bv = v-p2
    let Cv = v-p3

    let z1 = cross(AB, Av).z
    let z2 = cross(BC, Bv).z
    let z3 = cross(CA, Cv).z
    let z = [z1, z2, z3]
    let inside = all(z > 0.0) || all(z < 0.0)
    ifel(inside, 1.0, 0.0)
  }
  let ratio = cover/(divNum^2)
  [*fgcol.xyz, ratio*fgcol.w] |> to_u8color(...)
}

コードの説明はもういいでしょう。

無事キレイになりました。