MacKayのInformation Theory, Inference, and Learning Algorithms、6章〜
勉強会で読む事にしたMacKayの情報理論の本。
6章からのノート。
6章 Arithmetic codeとか
動画の方がわかりやすいのでまず動画を見る。
https://youtu.be/cJ_rhZ9DP9k
Huffmanコードのブロックがどうの、というのは、\(X^N\)を一つのアルファベットとみなしてエンコードする、というものだった。 当然場合の数は大量になるので、全部の同時確率を求めてエンコードしていくのはそれなりに大変。
arithmetic code自体は動画では大して分からなかった。テキスト読む方が良さそう。 exampleのtoss of bent coinをやるのが良い。
Arithmetic codingの効率について考える
Exercise 6.1は効率についての話だが、少しはしょり過ぎてて良く分からないので、もうちょっと素朴な所から考える。
まず、結局はn文字の何かをエンコードする。 それは究極的にはこのn文字の出方の確率に対し、式5.17、つまり\(l_i = log_2 (1/p_i)\)に振るのが理想。
一方でArithmetic codingは、
1.系列を、特定の実数の範囲に対応させる
- 1の確率の範囲は、この系列の実現しやすさをあらわす同時確率になっている
- decodeは、この範囲に収まる所まで調べたら終わる
というもの。 この3の長さが、どのくらい式5.17に近いのか?というのが知りたい事。
ちょっとノーテーションが要るな。 並べて割り振ったアルファベットのi番目の確率を\(p_i\)として、それを0側から並べた累積分布関数を考えた時に、iの始まりを\(\underline{p_i}\)で、終わりを\(\bar{p_i}\)で表そう。

上が0なのかややこしいが仕方ない。
デコードを終われる最短のビット数は、そのビット数で表される範囲がこの範囲に収まってる場合だ。 あるビットの列が表す範囲は、そこから0を無限につなげた物から、最後のビットを一つ増やした物の直前まで、という事になる。 この幅は、このビット列の桁の最後の数字の担当範囲となるので、1/2の桁数乗か?
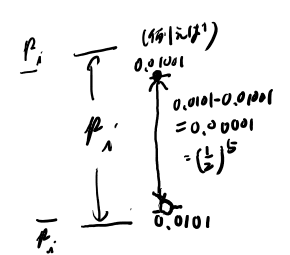
このビットの長さ、というのは、1/2をk乗した時に上記の範囲が最初にこの範囲に収まるkという事になる。
さて、この\(\underline{p_i}\)とかは都合よく2で割っていくと区切りが良いとは限らない(Ex 6.1など参照)が、ちょうど良いとすれば、この長さは、1/2を累乗していった時にちょうど\(p_i\)になる所だ。
これを変形すると、以下のようになって、
\((1/2)^{l_i}= p_i\) \(log((1/2)^{l_i} )= log(p_i)\) \(l_i = log_2 (1/p_i)\)
このコードは最適なコードになってる事が分かる。
さて、ちょうど良くないと端数の部分が出てくるが、これはちょうど2進数で余った範囲の期待値を取っていく事に相当し、たぶん余った幅に応じた長さの期待値となると思う。(長さにいつも同じだけの1/2乗が掛けられるので、極限はlogになる?)
だから無限に続くならこの端数は無視出来る。 無視出来ない影響は最後の一文字の所にだけ出るのかしら? それはEx 6.1だな。
6.4 Lempel-Ziv coding
簡単なバージョンの具体例を計算してみて、非効率な所を理解するのが良い。 6.4の例をエンコードしてみる。 この時長さの桁が毎回かわる事に注意する。
最適性の証明はCover and Thomasのノートの13.5.1を参照の事。