Elements of Information Theoryの十二章〜最後まで
Elements of Information Theoryの読書記録
という事で以下の本の12章から先を読んでいきます。
amazon: Elements of Information Theory (English Edition)
12章、Maximum Entropy
そもそもこの本を読もうと決意したきっかけがMEMMとかCRFでMEが使われてて、自分が全然知らなかった事だから、というのがある。 なのでなかなかモチベーション高い。
変分計算の公式
式12.2から12.3の変形みたいなのを、どう計算するか。
要するに一つ目の項だけ見ると以下。
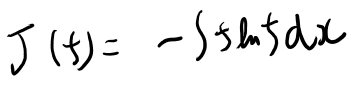
最終的に極値を取る関数がオイラー方程式で求まるのは良いとして、これの変分自体を計算する簡単な公式があるんじゃないか、と思ってた。
自分は良く分からないので、手持ちの変分の教科書に従い、定義から計算してた。
なおこの本は大変分かりやすく書かれてて、最初の10ページくらいで必要な事は全部わかる。そこだけpdfかなんかで配ってればそれで十分なんだが…ただそんな高い物でも無いので、そこだけの為に買う価値はある。
で、これに従い、1.1の公式6から計算する。
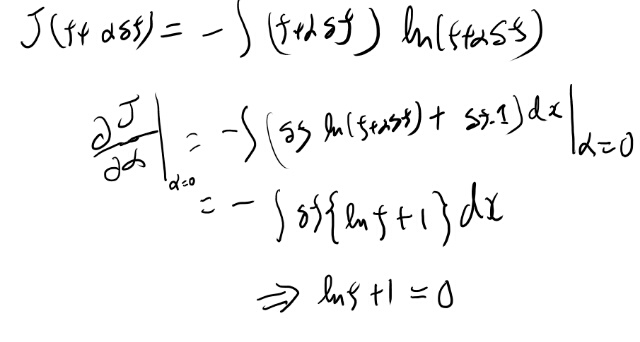
これなら隅から隅までなにをやっているかを理解出来ているのだけど、これを式12.2の各項でやってるとも思えない。
もっと簡単な方法があるんじゃないか?とslackで物理な人に聞いた所、以下のような公式で計算出来る、と教えてもらった。
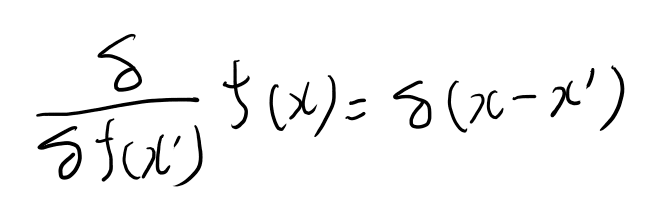
右辺のデルタはディラックのデルタ関数。 これで積分記号が消える。
これに従い式12.2を計算すると、
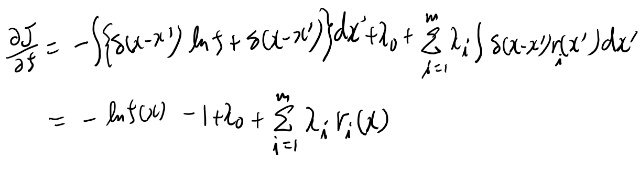
おお、これなら慣れれば暗算で出来そう。 これって昔どっかで見た記憶があるが、10年以上前な気がするのでたぶん学生の頃だよなぁ。全然覚えてない。
PRMLのAppendixを見ても上記の変分の本を見ても書いてないので、まぁまぁ知らない人もいるんじゃないか?これ。
というのは、結果だけ丸暗記ならオイラー方程式で良い。オイラー方程式の導出自体は定義に戻ってやれば出来る。 一方でたまにしか出てこないなら定義に戻って計算すれば良い。
ということで、この、間くらいの変分のルールって結構ちゃんと勉強してないと必要にならないから、あんまり解説される機会が多くない気がする。 そしてすごく使う人にとっては常識になってしまうのでますます語られない。
上記の公式は、本質的には普段自分がやってた計算をデルタ関数で記述しているだけなので、教えてもらえば、それを理解するのはそんなに難しい事では無い。一方でこれを知らないと計算は大変。
という事で変分レベルが1上がった(ファンファーレの音)
追記: この辺の計算が載ってる教科書とか知ってますか?と言ったら、菊田さんがググって以下を見つけてくる。 Density Functional Theory : An Advanced CourseのページのBack matterというappendix(ページの下にリンクがある)
これのAppendix Aは必要な事がすべて書かれている気がする。 ただちょっと知ってる人向け、って感じですね。前述の本を読んでからだとちょうど良いですね。自分にはちょうど良さそう(なお教科書はめちゃくちゃ難しそうで何についての本なのかも分からん…)
Approach2の計算を追う
大した事無いが一応追っておく。
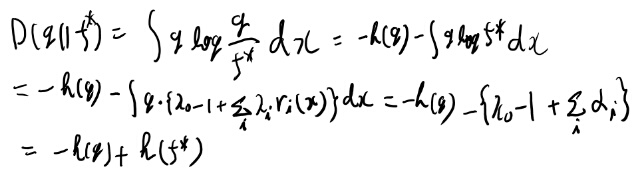
log fはfで期待値をとってもgで期待値をとっても値が一緒、というのがポイントか。
次の定理12.1.1でも同じ性質を中心に証明されてる。
ところで、- g ln kの形の期待値を最小にするdensity kは、gなんだろうか? もしそうなら、積分記号をさぼると、以下みたいなかんたんな式変形と解釈出来るが。
- g ln g < - g ln f = - f ln f
少し考えてみよう。
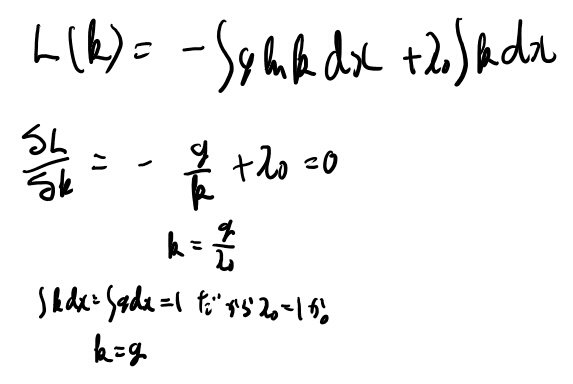
お、言えそうだ。こういうのスラスラ解けるのは変分レベル上がった感じするね。
でもこれは、ようするに12.6と12.7と同じ事か。 そのやり方も書いてみるか。
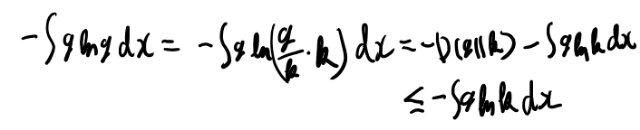
お、absolutely continuousじゃないとKLダイバージェンスが定義できなさそうだな。 こんな所で必要だったのか。
こういうの、実際にやって自分で気付けるのもなかなか理解深いな、と自画自賛。
例12.2.3のサイコロn投げる例がめっちゃ凄い!
サイコロをn個投げて目の合計がアルファでした、1の目のサイコロ、2の目のサイコロ、、、はそれぞれいくつずつでしょう?という問題。 こんな具体的な簡単な問題でこんな奥深い物が見れるのか、と感動した。
これを単純に、合計を元に、それが達成されうる各目を考えてその組み合わせを考える、という二重のfor文で解くのは簡単に出来るが、人間にはちょっと解けそうも無いし、それではなんの洞察も得られない。
各目がいくつ出るかを固定した時の組み合わせの数を、制約条件を元に最大化する、と考えるとこの問題は美しく解ける。この発想の転換は面白い。
これが12.19としてもとまるだけじゃなくて、このpスターのそばにほとんど全部の場合の数が集まる、というのも味わい深い。
こんな風にこの問題を考えられたらかっこいいなぁ。
12.2はなかなか面白かった
例がつらつら並んでるだけの節だが、思ったより面白い。 ちゃんと全部を消化出来てるほどは自分のものに出来てないが、 maximum entropyは一見すると雑すぎる近似に思えるが、含意はなかなか深い。 この節は読む価値があった。
12.6 burgの定理
少し間があいた(といっても数日だが)のでいろいろ忘れてる。復習しつつ読み進めたい。
つらつらと読んで行った所、Yule-Walkerの定理の所でわからなくなったのでメモを書いておく。
別段この話題に興味がある訳でも無いので、難しそうなら飛ばす、くらいの気分で。
Yule-Walkerの定理
Rがなんなのかが良く分かってない。 covarianceは普通行列で、要素は足が2つだと思うのだが、0からpまでのcovarianceとは一体?
読み直して見ると、12.4のスペクトル推計の所で同じ記号が出てきている。 これは何故iに依存しないのだろうか? それはstationaryという仮定からか。
つまりR(k)は、k個先のデータとの相関、という意味だな。
12.6に戻ると、stationaryだと時間のシフトで結果が変わらないので、p次のマルコフ過程ならある時点から前p個との相関で全covarianceが尽くせるな。
少し背景知識が足りない気がしたのでyoutubeの動画を見てみた。
youtube: Autoregressive Models: The Yule-Walker Equations
12.53までは割とちゃんと理解出来た気がする。
12.55が良く分からないな。 計算してみよう。
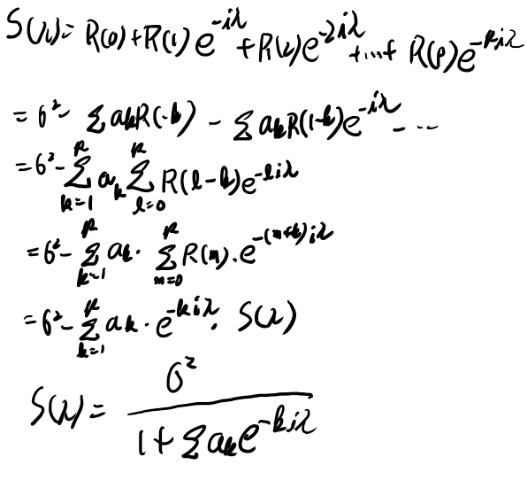
あれ?惜しいけど絶対値が出てこない。 多分なにか間違ってるんだろうけど、だいたいどういう感じかは理解出来たからいいか。
12章はなかなか面白かった
もともとME自体を知りたいというモチベーションはサイコロ本などですでに高かったので、割と楽しく読めた。 また、前の章のtypicalとかの話を前提にMEを考えるといろいろと違う視野がひらけて、ある種の感動がある。 学問とはこうありたいものだ。
後半のautoregrresive modelの話は、ちゃんと確率過程の教科書で勉強してから読まないとしっかりとは理解出来ないなぁ、と思った。 機会があったら勉強したあとにまたこれを読み直したい。
13章 Universal Source Coding
あまり興味は無いので、軽く流したい所だが、Channelとか忘れかかってて流し読みするのも一苦労。
Channel周りを軽く復習
7章はほとんどノートが無いが、2章は割とちゃんと計算してるので2章見直すと思い出す。 xの分布をいろいろ変えて、相互情報量の最大を狙うんだな。思い出した。
minmux redundancyとcapacityの関係
まぁまぁ難しかったのだが、メモを取らずに読んでしまった。 そのまま先に進もうかと思ったが簡単にメモをとっておく。
シータでパラメトライズされた分布があるが、シータが分からない、という時に、出来る最善のエンコードについて考えたい。
シータでパラメトライズされた分布とqの間のredunduncyは、そのqの-logで定義される長さlと真の最短の長さの期待値の差で定義される(13.2)。 それはKLダイバージェンスになってる(13.6)。
このRedundancyのmin maxでの最小値はminmax redundancyと呼ばれていてRスターで書かれる(13.7)
この最小を達成するqを求めたい。
そこで、シータを入力としてXが出力として得られるチャンネルを考える。 シータの分布を考えてそのchannel capacityを考えるというのはちょっとした発明だ。 そして13.9のように書けるのは、分子を同時分布にして、分母を「同時分布を別々にマージナライズして掛けた物」とすれば導出出来る。
で、そのcapacityはminmux Redundancyになってる、との事。(定理13.1.1)
証明のキモがわかりにくいが、13.17から13.18の所でiの和を取るとKLになってる、というのがポイントのよう。
証明はちゃんと理解出来ているかは怪しいが、使い方はなかなか分かりやすい。
例13.1.1がなかなか良い例で、p1とp2の両方に一番近い物は、まぁ同じKLの値になりそうで、それはqとなる。 こんな感じで、それぞれの分布の両方にKLの意味で一番近い分布を探すという問題になる。面白い。
13.2 バイナリ列のコーディング
最初の例は、k個の1がならんでるパターンを全部予め列挙してインデックスつけておく訳だな。 個数とインデックスの2つの数字で系列が記述出来る。
13.3 Arithmetic coding
まったく興味が湧かないが、トピックだけ追うのがやけに辛いので、概要を追うためのメモくらいは書いておく。
補題13.3.1は何度か証明したことはあるが、いまいち覚えてないな。 証明の式は分からない事は無いのでよしとして、もっと感覚的にも考えたい。
適当なランダム変数YのdistributionをUと置く。 Uの分布というのは、ようするにYの分布を縦軸側から見た時にどれが得られるか、という話だ。 それはどこでも一様に出やすい、と言っている。
そりゃそうか。任意のデルタuを考えた時に、このデルタuの範囲に収まる確率はいつでもデルタuか。
次の系列を小数と考える話、F1とかF2は2進数の展開か?わかりにくい書き方だが。
例13.3.2の図13.2がめちゃくちゃ分かりやすい。これだけみてなんとなく納得すれば良いんじゃないか。 ただこの例ではA, B, Cの確率がわかってるので、Universalな例では無いか。
例 13.3.2の実数値からのデコードをもう少し真面目に考える
MacKayの本の勉強会でArithmetic encodingの担当になったので、この例をもう少し真面目にやる。
まず、4文字とわかってるのかな。 で、0.3264、という数字が与えられる。 これをデコードする。
まず一文字目が0, 0.4, 0.8を区切りにした3つの範囲に切れる。 0.3264は0-0.4に入るので一文字目はA。
次に、二文字目は0-0.4を、また3つに分ける。 つまり、0, 0.16, 0.32, 0.4の3つの領域に分けられる。
0.3264は0.32〜0.4に入ってるので、二文字目はC。
次に0.32〜0.4を3つに分ける。すると、 0.32, 0.352,…と分けられるらしい。 0.3264はこの1つ目の領域なので三文字目はA。
この次もやると、Aと分かるらしい。 これで0.3264からACAAがデコード出来た。
例 13.3.2の、実数値へのエンコード
次はエンコード。といってもデコードが分かれば分かるか。
まずACAAと確率のテーブルが与えられてるとする。
Aなので最初の範囲は0-0.4になる。 次にこの領域を3つに分けて、Cなので0.32-0.4となる。
次にこの領域を3つに分けて、Aなので0.32-0.352となる。
次にこの領域を3つに分けて0.32-0.3328となる。 そこでこの範囲の中点を選ぶと0.3264となる。
例13.3.2の最適性を考える
図13.3のような段々を書く。この時、それぞれの実数値の実現する確率は、このインターバルの大きさとなる。
そこでこのそれぞれの実数値を、実現確率を使ってエンコーディングする。 実現しやすいシーケンスなら、大きな段を分けてたどり着くのだから大きな段となりやすい。そこで短いコードを割り当てられる。
段の大きさは系列の同時確率だ。 で、段の数はアルファベットの大きさのn乗だ。 これをコーディングすればいいんだな。
13.5.2は飛ばした
辛かったのと軽く読んでも概要が分からなかったので、ここは飛ばす事にする。 読まなかった事は記録しておく。
13は多分あんまり理解出来てない
一通り読み終わったし、最後以外はだいたいは式は追えたのだが、いまいち何も覚えてない感じなので、たぶんあまり理解出来て無さそう。 しかも結構難しい。
式の変形は追えたが流れを頭に入れる所までは行かなかった、という感じだなぁ。
ただ一応式は追ったので、必要な日が来たらある程度は思い出せる事を期待したい。
13.5.1 簡易版Lampel-zivの最適性について
MacKayの方の本の勉強会で当番になったので13.5.1を読み直した。 証明自体は教科書が良く書けているので、ここにはそれはを補足するような、気づいた事などを書いていきたい。
補題13.5.1 大きさkの整数をエンコードするコードの上限
大きさkの数値をエンコードするには\(log k + 2 log(log(k))+ O(1)\)あれば十分、という補題。
感覚的には長さが分かってれば2進数で表現するとlog kなのだからこんな要らない気もするが、なんにせよこれだけあれば十分なのはそんな難しくない。
要するに最初に長さを送って、そのあとlog kを送れば良い。 長さは何も考えずに最初の1が出る場所を長さとすれば、log kで送れる。 もちろんこれはめちゃくちゃ無駄が多いが、この長さ自体を同じ理屈のエンコードで送ると、logのlog kで送れるので、log log kのオーダーで長さが送れる。まぁそうだろう。
系13.73式を考える
Kacの補題とその系13.73まではこの証明の本体と思うし、一応一通り追ったのだが、
- 本質的にはガチのエルゴード性の話が必要(そしてそんなのは自分には分からない)
- 感覚的にそこをごまかすなら、式13.73自体がそもそも感覚的に解釈出来る
という事で13.73に対してのメモをここに書いて先に進みたい。
まずは記号の意味から。
ややこしいがこれは誤植では無くて\(x_0^{n-1}\)は、\(x_1x_2 \ldots x_{n-1}\)という系列を表していて、期待値は、0の時点での系列を所与とした時の条件付き期待値となってる。
そしてRは、前を見返していった時に最初に開始地点と同じ系列が現れた所のインデックス。
この期待値が\(p(x_0^{n-1})\)の逆数というのが13.73式だが、これはようするにこの系列自体をアルファベットと考えた時に、一つ戻る都度そのベルヌーイ試行をしていると考えた時の、ヒットする平均の距離のようなもので、これが幾何分布になってる、という事に近い。
もちろん現実はi.i.dじゃないし、むしろi.i.dじゃないからこそLempel-zivなんて事をする訳だ。
しかも\(x_0^{n-1}\)によってはそもそも-1とか-2とか-3とかの範囲は確率ゼロな場合もあるので、n-1の範囲ではconditionedされる条件と独立でも無い。 うーむ、そこはおかしい気がするな。jはn-1の所からスタートする方が良い気がするな。 だが本質的には情報としての長さが大切なのであって距離は大切じゃないから、n-1から始めれば良いと思う。
とにかく、長さnのブロックが与えられとして、これを過去に戻っていって同じブロックが出てくるまでの戻らなきゃいけないインデックスの長さの期待値は、幾何分布の期待値みたくなっていて、そのブロックの実現確率の逆数になってる、という事だ。
簡易版Lempel-zivの効率
長さnのブロックを送信する事を考える。 このブロックと同じブロックを過去に探して、そのインデックスを送る、というのが簡易版Lempel-zivだ。
このインデックスの整数をエンコードした時のコード長の期待値が送信時の長さの期待値だ。 この長さを\(R_n\)しよう。
こいつはブロック長を長くしていくと、エントロピーrateのn倍に漸近的には近づく、つまりoptimalというのが示せる。
これはまず13.76〜13.80でlogの項がEntropy rateになってるのが示せている。これはクリアなので良かろう。
log logの項は、1/n logがなんかの定数なのだから、1/n log logがたぶんゼロなのは良かろう。
という事でブロック長を大きくしていくと、漸近的にはentropy rateになっている。
14章 Kolmogorov complexity
面白そうなので興味はあるがなんだか難しそうだなぁ、という印象。 別に使うあては無い。
読んでみて難しそうならそんな頑張らずにギブアップしよう、というつもりで読み始める。
Ex 14.2.3のemprical markovtransitionをlog nのオーダーで書ける、というのはどういう意味だろう?
例えば1の次に0になるのが8回、1の次に1になるのが2回としよう。 これで遷移確率は0.8と0.2となる。 一般には長さがnならこの小数はlog n桁になるか。
なるほど、これを使ってxの同時確率を求めて、その確率に応じたbit長を割り当てればkraftの不等式を満たすのでエンコードしてやれる訳だな。 随分あっさりした解説だがなかなか難しいなぁ。
Ex 14.2.8はcombinationの不等式を良く分かってないのでなんだか良く分からない式変形に感じられる。 ただ並べてインデックスを示す、というのは理解出来る。
定理を理解するのは諦めて進んで見る。
14.3は分からなかった
式変形を丹念に追っていかないとこれは分からないなぁ。 ただそこまでやる気も無いのでぼへーっと眺めて先に進む事にする。
分かった具合メモ
全体的にメモのとりようが無い感じなので小学生並みの感想を。
14.5は割と理解は出来た気もするが、なんかしっかりわかった気がしない。こういう時はだいたい分かってない。
14.6はUniversal probabilityがそもそも良く分かってなさそう。 定理14.6.1のあとの解説が何を言ってるのか良く分からないので。
タイプライターをランダムに叩くよりはランダムに叩いたコードを実行する方が意味のある結果が出やすい、というのは全く理解出来てないが、本当なら凄い結論だなぁ。
14.7、14.8、14.9、14.10はお話が多い。 一応読む。
14.11は定理14.11.1の右辺の証明だけ追って、左辺はギブアップ。
14.12、kolmogorov sufficient statistic。全然分からん。ギブアップ。
14.13は一応読んだ。理解出来てるかは分からないが。
14章は半分以上分からんかった
めっちゃむずいね。 ただ本の解説自体が単にお話だけにとどまってるトピックもあったので、ちゃんと理解出来る類の事でもないのかもしれない。
具体的な論を追う事は出来てないが、どういう話なのか、というのはなんとなく理解出来た。 必要になったら本気でもう一度やろう。
つれづれ
15章のnetworkのcapacityなどは飛ばす。 使いそうな気もするんだが、もう気力が限界。
で、16章はportfolio。 この辺は昔結構やったので情報理論から見直すのは面白いかもしれない、と思い、読んで見る。
16.2.1の極限(eの定義)
\[e= \lim_{t \to 0} (1+t)^{\frac{1}{t}}\]16章雑感メモ
16.2で適当な系列の同時分布に対するlog optimalなポートフォリオの性質をやっている。
log optimalというのはasymptoticな富の増加を考える為に定義した物だが、キューンタッカーの定理から、ある時点までの同時分布を考えた時の富に対しても最適になっている(定理16.2.2)という話に見える。なんでexpected wealth relativaなんていい方をしているのかは分からないが(単にSの期待値を最大化する、ではダメなの?)
16.3からは系列を考える。まずはi.i.d。 Lemma 16.3.1のlog optimalなポートフォリオは期待値を最大化するのはほぼ定義そのまま。
定理16.3.1はちょっと分かりにくいが、期待値では無くて漸近的な同種の性質。
16.4は実際の分布と予想分布が違う場合の話。 growth rateの差はKLダイバージェンスになり、side informationによる改善は相互情報量で抑えられるという美しい結論。
16.5は16.3のi.i.dのケースをstationaryなケースに拡張する。 証明がきわどい条件を使い過ぎて、さらっと読むくらいでは全然ついていけない。 これは諦める。
16.6は有限の期間でのoptimality。 期待値が最適なのは良いとして、もっと強いことは言えないか?という話。
どんなポートフォリオ戦略でもそれをちょっと超えることがそれなりに良く起こる物は作れてしまうが、それはだいたいはそんなに大きく超える物では無い、という観測があり、それを元にcompetitive optimlityという概念が説明されている。
ちょっと一様分布とかをつけるといい感じにちょっとの差をランダムの要素に含められるらしいが、なかなかこれの妥当性を感覚的に納得するのは難しいな。諦める。
定理16.7.1の証明メモ
16.104を書き下すと以下。
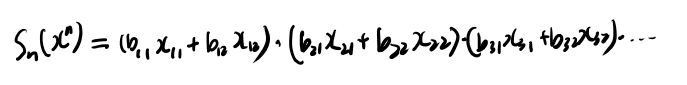
これを16.105ではどう書き直しているのか? 展開するとbの各iについてのどちらかの項がでてくる、xも同様。 それを記号で表現してるだけか。
16.106と107では、その式のうち、あるxの系列に着目しているのかな。それには対応するbの系列がある訳だが、それを一つの重みとみなす。
すると16.109は、比の下限は最悪の系列のweightで決まる、といっている。
16.113くらいまで追った所で挫折。まぁよく頑張った。
16章雑感
16.7.2は諦めて定理だけ眺めて次へ。 16.8は定理だけ眺めて終える。この辺は必要になるまでは逃げて行きていきたい。
最後の方は辛かったが、16章は何をやってるかは割と追えていた気もする。 今直接必要じゃない身としては、このくらいの理解で十分じゃないかなぁ。
それにしてもこの辺は難しいね。ちゃんと消化出来てる人はどのくらい居るのだろうか?
17章、いろいろな不等式
これまでやってきたことのまとめや関連する不等式が並んでる。復習程度に軽く見て、新しいごついのは証明は諦める。
定理17.7.2 de Brujin’s identityのメモ
証明の序盤で、ランダム変数とZとの和の密度が既知として出てくるが、知らない。この辺は実解析レベルを相当に要求してくるねぇ。
少し考えてみたら、X+Yのlawがconvolutionになるのは有名な話なので、その関係から導出できる気はする。 納得出来たので先に進む。
続きのメモ
17.9は眺めた。あまり理解する気は無かったが、思ったより筋は追えた。 線形代数的な不等式の情報理論的な証明はちょっとおもしろいね。 この辺修得すると何か良い事はありそうだが、今回はそこまでは無理だった。
17.10はギブアップ。まぁこれはいいだろう。
全体の感想
読み終わった!頑張った!ということで全体の感想とか。
まず、7章のChannel capacity、9章のガウシアンチャンネル、15章のNetwork information theoryはほとんどやってません。
また、10章のRate distortion theory、14章のkolmogorov complexity、16章のポートフォリオあたりは理解度低めだが、でもあらすじくらいはちゃんと追えてる気はする、くらいの状態での感想です。
大変勉強になった。正直こんなに勉強になると思ってなかったので、良い意味で驚いた。
この本は通信以外の話題が豊富で、しかもなかなか難しい所もそれなりにちゃんと扱うので、その分野の広がりみたいなのを察する事が出来る。
typicalとかAEPみたいなのはとても勉強になったし、Maximum entropyみたいな、ちょくちょく出てくるが全然わかってなかったトピックも完璧に理解出来たと思う。
相互情報量周りの経験もいろいろ積めて、大分イメージ出来るようになった。 機械学習屋としては十分以上にこの辺は理解出来たんじゃないか。 もうこの分野の話題なら何が出てきても、出てきてから頑張る、でどうにかなる、くらいの自信は得られた。 詳しい分野が一つ増えたという満足感がある。
予想よりもトピックが幅広かったおかげで、当初心配してた、あまり興味のない通信の話ばかりなんじゃないか、という問題は杞憂だった。 通信周りの話ももちろんあるが、割と情報理論の本質的な事を理解する題材くらいに抑えられていて、機械学習屋として知りたい場合にちょうど良いくらいになっている。
必要な数学は、測度論は使わずに書かれている、とは主張してあるし、実際まぁあまり使われていない。 ただ内容的にはかなり進んだ確率論が無いとついていけない事がそこそこ含まれているので、内容のだいたいを消化したいと思えばもっと先の数学まで要るだろう。
逆に測度論を避けるせいで、何を言いたいか分かりにくい所も多少はある。 個人的にはちゃんとした言葉で記述してくれる方がずっと楽に読めただろうになぁ、とは思った。
ただ、そういう場所は序盤におもったほどは多くなかった。全体の2割くらいに収まってる気がする。 結構がんばって書いたなぁ、と賞賛の気持ちが湧く。
思っていたよりは大分難しい本だった。 ちょっと始める前は甘く見てたが、数学的には結構高度な内容だ。 実解析は必須では無いがやってる方が良いし、変分とかもそれなりに詳しくないと一部つらい(自分は分からず物理の人に教えてもらった)。
ただ、難しい所は諦めても、それ以外の所だけでも多くを学べる本なので、自分の実力と必要に合わせて読める本だとは思う。
全体としては読んで良かった。やはり機械学習屋はこの辺一度はがっつりやっておく方が良いね。