MacKayのInformation Theory, Inference, and Learning Algorithms、1章〜5章まで
勉強会で読む事にしたMacKayの情報理論の本。Cover and Thomasと並びよく参照される情報理論の定番教科書。 こちらにはベイズと機械学習の話題がある。
Kindle版は無いが、pdfがある。
Information Theory, Inference, and Learning Algorithms
一章
最初にスターリンの公式と二項分布がある。 準備体操に手を動かしてみるか。
Example 1.1 偏りありのコイン投げ
表かfのコイン投げ。N回投げて表がr回出る確率と、rの平均と分散を求める。
まずは表がrの確率。
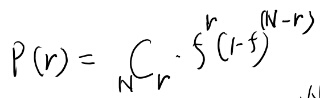
右下にごみが入ってるが気にしない。 次は平均。
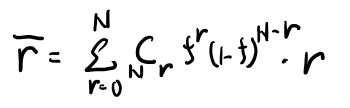
これどう計算するんだっけ。二項定理使って微分すれば出そう?
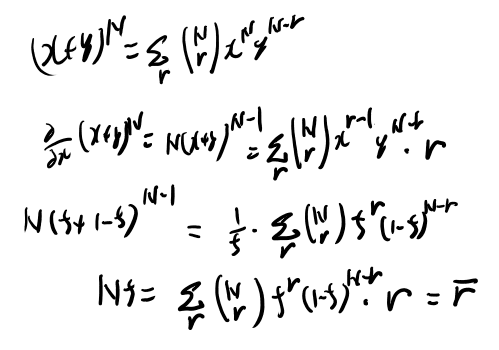
ふむ、Nfか。まぁそりゃそうだな。解説見ても一回の平均がfだからN回でNf、としてる。
次は分散。
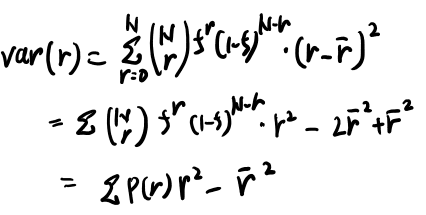
rの二乗の期待値を求める問題に帰着された。試行が独立なら別々の期待値の和だよな。r二乗の期待値は…1を二乗しても1だからfか?
すると、\(Nf-Nf^2\)だから、\(Nf(1-f)\)か。
スターリンの公式の話
コンビネーションの計算をしておく。
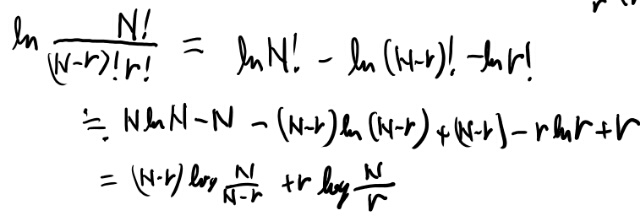
binary entropy function
Cover and Thomasでかなり混乱した所なので、少しメモを書いておく。
1.14で定義されるbinary entropy functionは、普通のエントロピーの定義とすごく似ているが、引数が違う。
普通エントロピーは確率変数に対して定義される概念だが、このbinary entropy functionはベルヌーイ分布のパラメータの関数になってる。
もちろんこのパラメータで分布は決まり、その分布に従って求めたエントロピーにはなってるのだが、気をつけないとすぐに良くわからなくなるのでメモを書いておく。
講義の動画
以前寝ながらこの教科書の講義を見てた事があるが、内容はだいたい同じだな。
youtube: Introduction to Information Theory
1章読み終わり
ハミングコードとshanonのlimitの話で終わり。 この辺はまぁだいたい分かってるのでバンバン進もう。
2章、確率、エントロピー、推論
序盤は確率論の話。 ensembleというのは初耳だが、複数のとりうる状態があって、そのうちの一つの状態が出てくる、みたいな問題設定っぽい。
数学的には離散的な確率空間は、アルファベットごとの重みさえ分かれば全て分かるから、空間としてそれらで示す、という事のよう。
2.44式はどういう定義か?
Hの分解について書いてあるが、右側の定義が良く分からない。
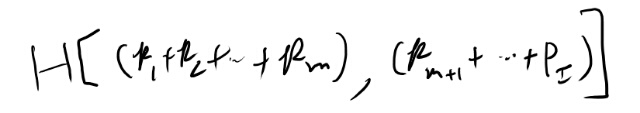
例えばmまでの和が3/4、そこから先の和が1/4とすると、定義はこうか?
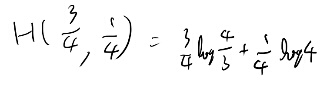
なんかこれっぽい気がするな。 記号は不思議な感じだが、1か2か3か…かmのどれかなら1、それ以外なら0の確率変数のエントロピー、のようなものか。
離散的な分布の時にprobability massを引数に列挙する、というノーテーションを導入してる訳か。なるほど。
3章 Inferenceについて
ちゃっちゃか進もう。
最初になんか解いてみろ、と書いてあるので、3.1を解いてみる。
Ex 3.1 二種類の20面ダイス
まだ何の章なのかも良く分かってないが、とりあえず解いてみよう。
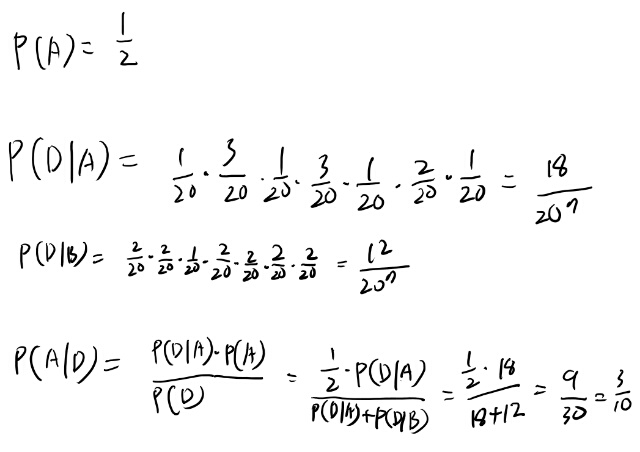
うーむ、なんか別段新しい事も無いような。 この問題の主旨はなんだろう?
Ex 3.3 decay定数の推計
このあとでこの問についてのエピソードから本題が始まってるっぽいのでこの問題だけ解いておく。
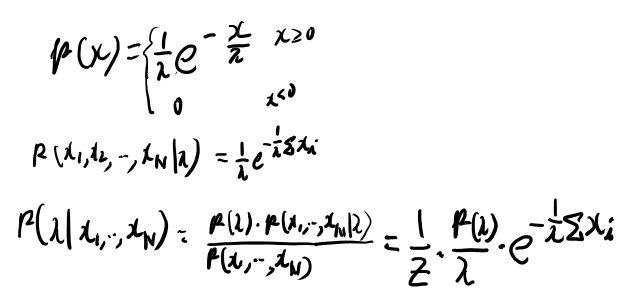
事前分布がわからんな。どうなってるんだろう? このくらいやっておけば本文は理解出来そうなので本文に戻るか。
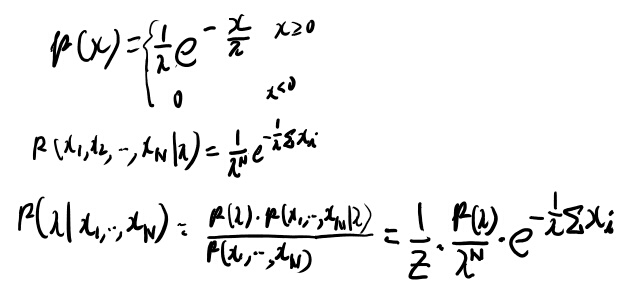
3章はいらなさそう
3.1を読んでいったら、ベイジアンへの批判とかについての話だった。 もうそういうのはいいよ、と思ってる身としては読み飛ばす事にする。
3.2は3.3のためのお膳立てくらいであまりノートをとる事は無い。(追記: と思ったが、あとでbent coinは良く出てくるので基本的な式だけメモしておく)
3.3はmodel comparison。 仮説H1とH2のどちらがいいか、を知るための話。
PRMLでやったし大してわからん事も無いが、エビデンスの定義を書いておいて先に進む。
他特に読む事は無さそうなので3章は飛ばす。
ベータ分布についてのメモ
pdfに書き込みしてたが、Bがガンマで書ける所の証明が手元に無かったので証明する事に。そのメモを置く場所が無かったので、ここにおいておく。
まず基本的な式。

ガンマが階乗になるのは部分積分から漸化式になりそうなのでまぁいいだろう。
Bは正規化定数になってるが、これがガンマ関数で書けるのは自明じゃないのでここだけ計算してみる。 これはPRMLの問題2.5になってて、結構親切なヒントがついてる。
この手の練習問題にちゃんとヒント書いてある所がPRMLがそのほかの本と違う所だよなぁ。すばら。
で、そのヒントは以下から始めて変形していけ、と書いてある。
\[\Gamma(a)\Gamma(b)\]必要な手順が軽く書いてあるので、そのヒント通り変形していく。
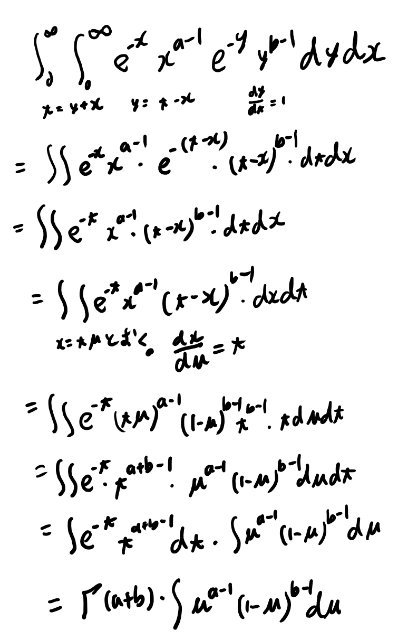
エビデンス
3.3であったエビデンス、すぐには定義が思い浮かばなかったのでメモしておく。
データDがあった時に、
\[P(D |\mathcal{H}_1)\]をモデルエビデンスと呼ぶ。 観測されたデータがそのモデルをどのくらい好むか、という値。
4章、The Source Coding Theorem
最初にex 2.21-2.25をやれ、と書いてあるが、単なる期待値計算とかで別段難しい事も無い。
とりあえず読む前に解けといってるEx 4.1を考えてみよう。
練習4.1 一つだけ変なボールと秤
問題を定式化してみよう。 秤はランダム変数Yとして、左が重いと0、右が重いと1とする。
個々のボールも確率変数とするか。 X1からX12。で、値は-1か0か1を取る。 11個の0と一つの-1か1の値、という制約条件。 ベクトルとしてはXと書く(フリック入力の都合)
どのボールが変かは分からないのでuniformなpriorとしよう。 うーむ、そうすると確率変数は、 どのボールが変かを表す方が良いか? 確率変数Tでどのボールがおかしいかを表すとしよう。これは1から12のどれかの値をuniformに取る。
さらにおかしいのが軽いか重いかを表す確率変数Wもあるとする。軽いと0、重いと1だとするか。
どの確率変数を使うかはわからんが、この位で進めてみよう。
何も試す前のエントロピー(試行0と呼ぶ)
知りたいのはTとWだな。 秤で測る結果との相互情報量みたいな概念にできそう?
とりあえずH(T, W)について考えよう。 これは、
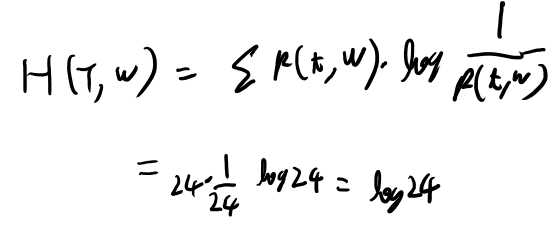
で良さそうか。
試行1-1 6個ずつかけてみる
うーん、どう考えたらいいんだろう。 まず適当に天秤にかけてみるか。 まず6個6個で天秤にかけるとする。 1, 2, 3, 4, 5, 6を左、7以降を右でかける。
左が重かったとしよう。 可能性としては、
- Wが重くて(1)、Tは左
- Wが軽くて(0)、Tは右
の2つに絞られた。 場合の数は6+6で12で、ぜんぶ確率は同じか。
この時のエントロピーを計算してみよう。
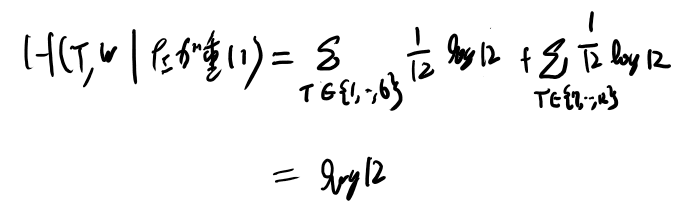
ちなみにこの場合は右が重くてもまったく同じだな。 これをゼロにすれば良さそう。
試行2-1 左の6個を3-3に分けて掛ける
最善かはおいといて、次は1から6を半分に分けて秤にかければ、Tは1から6か、7から12かのどちらから判明するな。 特定のWについて、p(T)がゼロじゃないのを集めて半分に分けて測っていけばだいたいわかりそう。
だが、これは最適じゃなさそうだな。 というのは、ハズレた時に反対側の方の情報がいまいち得られないから。
試行2-2 偶数番目を左、奇数番目を右に載せる(6-6で測る)
では、例えば次に、左に1, 3, 5, 7, 9, 11を、右に2, 4, 6, 8, 10, 12を乗せるとしよう。
今度は右が重かったとする。 Wは相変わらずどちらかは分からない。
- Wが重い(1)、重いのは2, 4, 6のどれか
- Wが軽い(0)、軽いのは7, 9, 11のどれか
この実験ならどっちが重くてもエントロピーは変わらなさそう。この場合のエントロピーを求めてみよう。
場合の数は6通りで全部確率は等しそう。
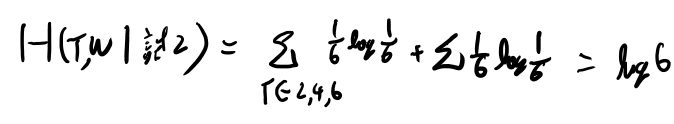
試行2-1を計算してみる
では先程の、1から6を半分に分けるのを試行2-1と呼び、試行2-2とどっちがエントロピーを下げてるか計算してみよう。
試行2-1は、
- 左が下がる
- 右が下がる
- 釣り合う
の三通りが考えられる。 それぞれどういう場合が考えられるだろう?
- Wが重くてTが1, 2, 3か、Wが軽くてTが4, 5, 6
- Wが重くてTが4, 5, 6か、Wが軽くてTが1, 2,3
- Wがそれぞれの場合でTが7以降
これは試行1と矛盾してるのがありそうか?
Wが軽いとTは7以降だから、Tが7以降はWが軽い場合に限られる。
Tが6以下ならWは重い場合に限られる。 以上を考慮に入れると、
- Wが重くてTが1, 2, 3
- Wが重くてTが4, 5, 6
- Wが軽くてTが7以降
になる。場合の数は12通りか。
試行1の改善を考える
エントロピーの期待値を計算してみてもいいのだが、その前に、秤が必ず釣り合う試行はいまいちな気がしてきたな。 感覚的にはYの系列は毎回なるべく3通りの確率が同じになる方が良さそうだよな。
最初の試行に戻り、12個のボールでYが三通りに等しい確率となるためにはどう載せたらいいか?
どっちかに傾く確率と傾かない確率を1/3で分かれるようにする為には、傾かない確率が1/3なら良さそうか。 これはTが除けた方にはいる確率が1/3ならいいのだから、4つ除けたら良さそうか?
だから1〜4を左、5〜8を右、9〜12を載せない、としよう。これを試行1-2と呼ぶ事にする。
これを定式化すると、T, WのjointなエントロピーとYのエントロピーを考えて一番減るYを設計するのが良さそう。 つまり、T, WとYの相互情報量を最大化すれば良さそう?
T, WとYのベン図を描いて考えると、、、こうか?
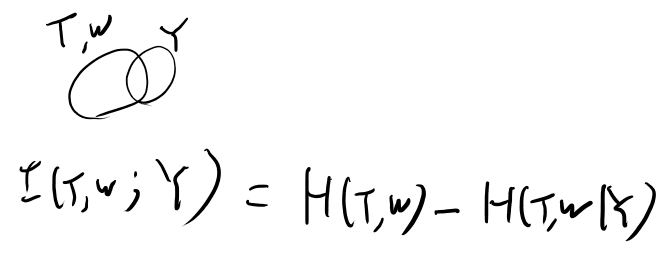
つまり、Yがgivenの時のエントロピーを最小化すればいいのか。
エントロピーが低いがYをどう頑張ってもあまりかぶるように出来ないという状況はあるかもしれない。 そうすると、各回の条件突きエントロピーを最小化する、というのは、いつも最適では無い可能性もありそう。 だが、そこはまぁ無いと思って進めるか。
条件付きエントロピーの定義を書いておこう。
| $$H(Y | X) = \sum p(x) H(Y | X=x)$$ |
| $$ = - \sum p(x, y) \log p(y | x)$$ |
試行1-2の条件付きエントロピーを求める
場合の数を考えよう。Yが左に傾いた場合、Tは8通り、右に傾いた場合も8通り。 それぞれWの値はTの値を決めると決まるから場合の数はこれで尽くせている。
さらに釣り合った場合はTが4通りのWが二通りだからこれも8通り。 全部同じ確率かな。
とすると、条件付きエントロピーは、
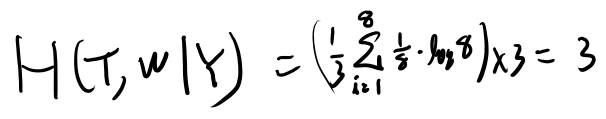
お、これは小さそう。参考の為に試行1-1の条件付きエントロピーも考えてみよう。たぶんこうか?
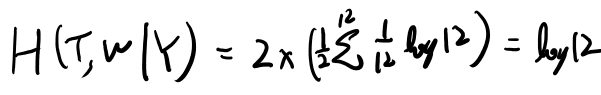
やはり少し大きいな。 log 8が最小かは良くわからんが、かなり小さい気はする。
Yでは一回ごとに3つに分ける事しかできないのだから、24が3に分かれて8になってる試行1-2は最適っぽい気はする。
エントロピーとyes noについて考える
最初のlog 24というのは、4と5の間くらいだよな。 だいたい4.5としておこう。
これはyes noの質問を5回すれば不確定性が取り除ける、という話だった気がする。
では1, 2, 3の三択問題では?というと、底を変えるといいのか?
\[log 24 = \frac{log _3 24}{log_3 2}\]だっけ。幾つか?2.9くらいっぽい。
じゃあ三回で当てられたら最適になってそう。
試行1-2でlog 8まで下げられている。 あと二回だな。
試行1-2の続き、つりあった場合を考える(試行2-3)
感覚的には、場合の数が三等分になるようにしていくのが一番効率的になりそう。 1-2で釣り合った場合は、Tは最後の4つのどれかでWもどっちか分からない。
感覚的には2, 2に分けちゃうと釣り合わないので、1, 1に分けて、2つ除けておく感じだな。 これを試行2-3と呼ぼう。
これで条件付きエントロピーは、釣り合った場合が一番分からなくてTが2択でWも二択の四通り、左が重ければTが二択でそれぞれ対応するWが決まるので二通り、右が重くても二通り。
それぞれの場合は場合の数あたりに等しく起こるとすると、釣り合うのが1/2の確率、残りが1/4ずつか。
これを元に条件付きエントロピーを求めると、
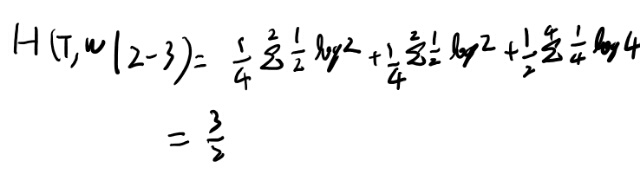
たぶん釣り合っちゃったらもう二回必要だな。 これが1/2で起きちゃうのはあんま最適っぽく無いな。
試行2-4 問題無い3つと比べる
例えば3つを、問題無いとわかってるのと比べるとどうだろう?これだと、釣り合えばTは一つに決まる。
釣り合わないと、Tは三択だが、Wは決まる。だから三通り。
条件付きエントロピーを計算してみよう。
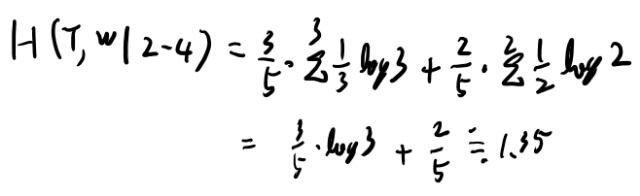
1.5より小さいのでこっちの方が良さそうだな。
釣り合えば候補は一つなので普通のと比べて終わり。 釣り合わなければTが三択だが、Wはどちらかに決まってるので、三択のうち2つを比べれば答えが出そう。
例えば対象の3つが重ければ、このうち2つを比べて、傾けばそちらが重いで答え、つりあえば除けた一つが重い、で答え。
どの場合でも三回で当てられるので、多分これが最適っぽいな。
1-2で片方が重かった時(試行2-5)
1, 2, 3, 4が重かったとして一般性を失わないだろう。 Tは1から8のどれか。
感覚的には、両方から同じだけ除ける方が良さそうか? 例えば4と8を除ける。この場合は釣り合ったらエントロピーは1だな。少なすぎるが、起こる可能性は2/8なので1/4か。
1, 2, 3と5, 6, 7をどう秤にかけたらいいだろうか? 例えば全部片方に載せる、、、と普通の重さが足りないか。4つしか無いからな。
たとえばもしあったとするとそれは最善なのか?重ければTは三択、軽くても三択、Wは決まる。だからエントロピーはlog 3か。これは一回でいけそう。
ただ4つしか無いのでそれは出来ない。 では、1, 2, 3, 5, 6を片方に乗せて、もう片方に7と普通のを載せる。 これを試行2-5と呼ぼう。
1, 2, 3, 5, 6が重い場合は
- 7が軽い可能性
- 1, 2, 3のどれかが重い可能性
の二択になる。場合の数は4か。 これは二回必要なのは避けられないか。
1, 2, 3, 5, 6が軽ければ、5, 6が軽いか7が重いかで、場合の数は3。これは5, 6を比べれば一発でわかる。
試行2-6
うーむ、いまいち。1, 2, 3, 5, 6が重い場合が良くないな。 3も除けるとどうだろう? つまり3, 4, 8を除ける。
そして1, 2, 5, 6と7普通混合を比べる。 これなら釣り合ったケースは3択、3, 4を比較すれば一発でわかる。
1, 2, 5, 6が重い場合も
- 1, 2が重い
- 7が軽い
なので三択。 お、出来たな。
つまり試行1-2で1, 2, 3, 4側が重かったら、3, 4, 8を取り除き、1, 2, 5, 6と7そのほか混合で比べる。 これを試行2-6としよう。
答えと雑感
試行1-2をまず行い、釣り合ったら試行2-4を行う。 傾いたら試行2-6を行う。 逆に傾いた場合の2-6’も本当は述べる必要があるが、まぁいいだろう。
これはT, Wのエントロピーと、相互情報量の話になってるが、これって4章でやる事なのでは?最初に解けると4章やる意味が無いのでは…
感覚的には、等しく起こる場合の数が最初にあって、それを天秤にかける都度3つのグループに分けられる。 おのおのの場合の数を等しくしておけば、\(log_3\)回で一つに絞れるので最適っぽい気はする。
この場合の数をフィルタリングしていく感じは4章の話題の本質っぽいと思うので、最初に見ておくのは良いかもしれない。
AEPの手前まで読む
圧縮の定義みたいな話からtypicalの話に進む。 驚いた事に、内容的には冒頭の問題は解いてる前提だった。ここまでの内容では解けない気がするんだが…
ただ、Cover and Thomasでこの辺ちゃんとやった自分からすると分からない事は無い。 例が多いのは良いと思うが、あとから読み直す時には要点はわかりにくいなぁ。
あとPDFの目次の出来が悪い。Cover and ThomasのKindle版はこの辺抜群に良く出来てるので、相対的に辛い。ただ誤植は圧倒的にこっちが少ない。
4章概要
pdfに書き込みつつ読み直している。 pdf書き込みはスペースが足りなくなる事が多いのが難点だが、気分よく復習出来るよな。kindle本でも出来たらいいのに。
概要を理解したのでここにも軽くメモしておく。
4-1 information content
Shanonのinformation content(以下IC)の定義と、それが様々な例でどんな値になるかを見る事で情報の指標として適切な事を見る。
4-2 Data compress
ここでは圧縮とはどういう物かを見つつ、ソースのICと結果の記録に必要なbit数の関係がある事を述べる。またアウトプットの種類から下限を求める。(\(H_0(X)\)の事)
次の導入としてlossyとlosslessの定義も。
4.3 essential bit content
lossyな圧縮を題材に、essential bit contentという\(H_\delta(X)\)の定義と、それが漸近的にはデルタに依存しなくなりそう、という話をしてる。 だいたいの物が入る最小の集合がありそう。
そして最後にShannonのsource coding定理が、証明なしで述べられてる。 それは以下の量が、
\[\frac{H_\delta(X^N)}{N}\]がだいたいH(X)になる、というもの。
4.4 typical とAEP
二項分布を例にtypicalという概念やAEPを眺める。
4.5の証明は、簡潔だが微妙に筋が追いにくいので、記述をヒントに自分で考える方が早い。
5章 Symbol Codes
5章は実際のコーディングの話。 この辺はCover and Thomasとあまり内容が変わらないのでメモすることはあまり無い。
5.1 Symbol codes
cやlの定義やprefixコードの定義、例などが出てくる。
一つ一つのシンボルにコードを割り当てるもの。
5.2 Kraftの不等式
証明が良く分からない。Cover and Thomasを先に見直そう。
だいたい理解出来た。pdfに書き込みしたのでこちらは意味あいだけ。
ユニークにデコードできる為には、5.8式を満たさないといけない、というのが5.2の内容。
5.3、5.4 長さの期待値の下限と上限
下限は、
- 長さの期待値の定義の式に
- 長さから定義されるimplicit probabilityを代入して
- クラフトの不等式を適用して
- KLダイバージェンスが0以上で変形
していくと、エントロピーで抑えられる。
上限は実際に小さめのコードを作って、その値を上限とする。 それは以下のような長さ。
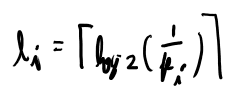
これはKraftの不等式を満たしている事が確認出来るので、これを実現するコードは存在する。
このコードによる期待値は簡単に計算出来て、それが上限になってる。
5.5 ハフマンコード
ここまでで、最適なコードの条件が分かったので、ここでは実際に最適なコードの一つの実例としてハフマンコードを解説している。
アルゴリズムは見たまんま。ただ、最適性の証明はExercise 5.16になっているが、回答を読んでも良く分からなかった。
そこでCover and Thomasを参考に自分なりに証明を書いてみた。別ページに分ける。
1Mb超えたのでノートを分ける。