Elements of Information Theoryの三章〜八章
Elements of Information Theoryの読書記録
2章だけのノートで1Mb越えてしまったのでエントリを分ける。
という事で以下の本の3章から先を読んでいきます。
amazon: Elements of Information Theory (English Edition)
3 章 Asymptotic equipartition property
日本語にすると漸近的等分配の法則、か?
内容としては、iidな確率変数をたくさんサンプリングすると、その同時確率のlogはHの-n倍になる、という物。
ベルヌーイ試行での例が書いてある。 n個のサンプルを取る。 その組み合わせによる実現しやすさは、もちろんデータの組み合わせごとに異なる。
だが、「n個のサンプルをとって同時確率を求めた値」は、高確率で2の-nH乗に近い、との事。
近いとはどういう意味か?とかいう気もするが、そこはおいといて、この法則の意味する所が良く分からないな。 なんか学部生の頃等分配の法則って統計力学とかでやった気がするが全然分からなかった思い出が蘇ってきた。
ほとんど表しか出ないコインを投げる。 エントロピーはほとんど0となるが、ちょっとだけ正の数だ。
すると、n回コインを投げたらだいたい全部表だよな。 その確率はほとんど1だが、nを大きくしていくとちょっとずつ下がる。
表の確率をpとして0.99としよう。 10回全部表の確率は0.99の10乗となる。
式3.1を考えてみよう。 ここから少し乖離した事象とはなんだろう? それは一つだけ裏が出る、という事象だよな。
つまり3.1が言ってるのは、全部表と一枚だけ裏、でだいたい起こる事の全部が含まれるよ、と言っているのか。
確率変数の収束
以下の3つの収束の定義が載ってる。
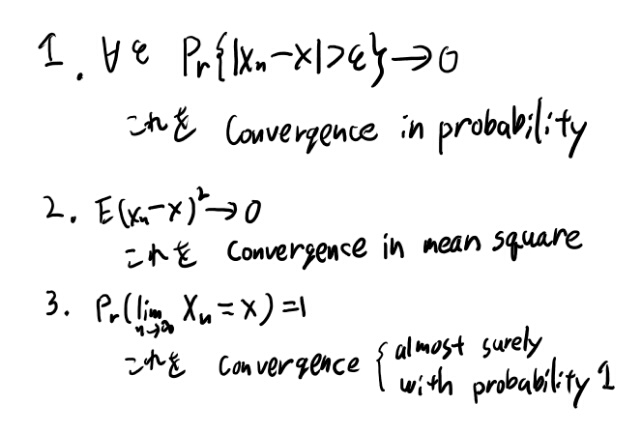
他の本も見直しておこう。
Dudley ではp261で1番目と3番目の定義がある。 Dudleyでは、確率1で起こる事象をalmost surelyに起こると言う、と言っていて、YnがYに収束する確率が1なら、 converge a.s.と言っている。
もう一冊、共立出版の「ルベーグ積分から確率論」も持ってるので見ておこう。
共立出版の方では、p117でa.s.の定義があるな。 こちらは「ほとんど確実に成立する」という言葉を使ってる。
in probabilityの方はp122で、確率収束、という言葉で紹介している。 また次のページに、p次平均収束というのも載ってる。書き方は違うが本書のin mean squareと同じ話っほい(こちらの定義はLpノルムによるバナッハ空間、という話にちょっと触れているのでもうちょっと厳密か)。
3.1 AEP定理
定理は単純に、独立なら同時確率の積になるので、logの同時確率が積になって和になって大数の法則で証明出来る。 自分で少し考えた時もだいたいそういう事だな、と思ったのでこの証明は納得出来る。
次にtypical setの定義がある。
typical set
typical setの定義は以下。

何も書いてないが、i.i.dかな。大文字のXはこの一つのxに対応する確率変数か。
定理3.2.1 コーディングの平均長
導出のところで以下のイプシロンダッシュが任意に小さく出来る、とあるが、分からん。
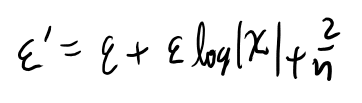
logのXってnを大きくすると当然大きくなる。 だいたいlog nに近い感じで大きくなるのでは?
するとそれにイプシロンを掛けた物は、nを大きくしていくと小さくなるか?は全然自明じゃない気がする。 逆に任意のaに対して、大きいn を持ってくればイプシロンダッシュをaより大きく出来てしまうのでは?
いや、良く見るとこのギリシャ文字のXは、nがついてないな。この定義はなんだろう? あぁ、一個のランダム変数Xの濃度か。それがn個並んでるからn logなのか。なるほど。 確かにこの濃度はnには依存しないな。
これがイプシロンで抑えられるのか。なるほど。理解した。
良く噂で聞いてたコーディング長の話はこういう奴なのか。クリアで面白いね。
3.2までの自分の理解
typical setは、だいたいそれが出る、という系列を表していて、数はまぁまぁ少ない、という性質がある。 特にnを増やしていくとほぼその中に含まれる確率は1となる。
このtypical setの数は少ないので、それをコーディング出来る長さと、typical setかどうかを識別するビットでだいたいは平均のコーディング長となる。
コーディングうんぬんはおいといて、このtypical setの濃度は低くてしかも確率はだいたい1、というのが面白い性質だね。 これはいろいろ使えそうな気もする。
4章 Entropy rates
さらさらと読んでいけるので、理解するだけならあまりメモする必要も感じないが、そうするとあとで必要になった時に困りそう。 という事であとで使いそうな範囲でメモするか。
4章は確率過程なのでi.i.dじゃなくて依存がある時の話。
Stationaryの定義
確率過程がstationaryとは、以下の性質を満たす事である。
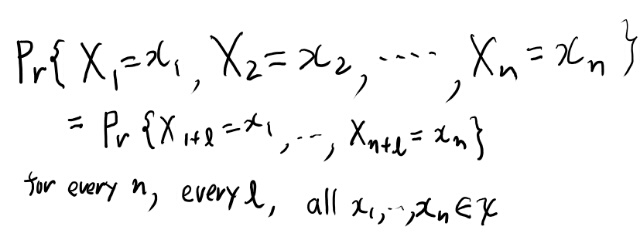
特定の系列のでやすさは、開始時点に依存しない、という事かね。 任意のlで成り立つ、というのは結構強いな。こんな強かったっけ?あんまり覚えてないな。
4.2 Entropy rate
エントロピーrate の定義は以下。
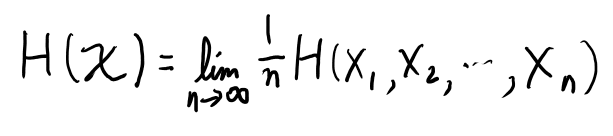
また、以下の極限も存在して、両者は一致するらしい。
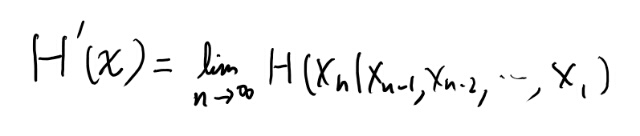
極限が存在するのは非負な減少列だから。 で、極限が存在するものの平均は極限になる、みたいなのと合わせて証明出来る。 感覚的にも積の法則でバラせばまぁまぁ納得出来る。
4.2.4 stationary markov chain
証明が理解出来なかったので自分でやってみる。 stationaryなマルコフ連鎖なら、真ん中の項になるまでは、少し上にわかりやすい途中式がある。
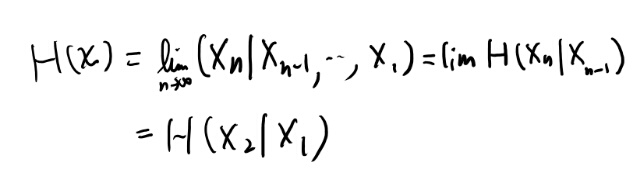
この最後の条件付きエントロピーを計算してみよう。
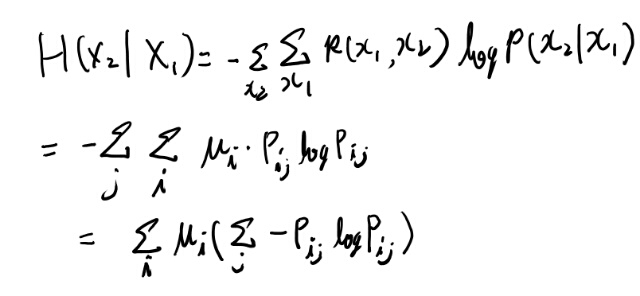
お、大した事無かった。Pijが条件付き確率になるのか。 まぁこういうのはたまに定義に戻って計算しないと分からなくなるので、こうやって計算するのは必要な事だ。
4章は簡単だがなかなか面白かった
さらさらと読み終わってしまい別段難しい事も無かったが、なかなかおもしろかった。特に最後のマルコフ連鎖の関数のentropy rateのboundを考えるのは簡単な計算なのにこんな一般的な事に面白い結論がでる、というのは驚きだ。
個人的には、この本はそこまで直接的な興味が無い所はさらさら流していくのがいいんじゃないか、と思った。 頑張って全部理解するよりは、サラサラ流して、もう一冊のMacKayの本も読んで見る方が良い気がする。
5章 Data Compression
ここは教養としてサラサラ読もう。 メモをとるのもサボりたいが、定義がいっぱい出てきて辛くなってきたので読み進めるのに必要な程度メモる。
Extension
Xを有限個並べた列からDの有限の長さへのマッピングで、以下のようなものをCode Cのextensionと呼ぶ。
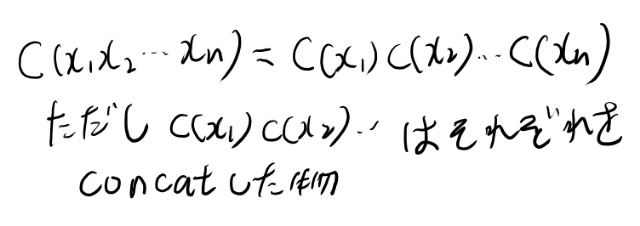
nonsingular
以下のコードを、nonsingularと言う。
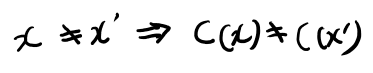
extensionがnonsingularな事をuniquely decodableと呼ぶとか。
普通に考えたらextensionじゃないコードでもuniquely decodableなものなんてありそうだが、そういう時は呼ばないのかな?ほんまかいな。
instantaneous code
どのcodewordも他のcodewordのprefixになってない事。
prefix code とも呼ぶらしい。どっちかというとno prefix codeと呼ぶべきもののような気もするが…
定理5.3.1はcが1より大きいじゃなくて1/cが1より大きい、だね。
D-adic
定理5.3.1の下に定義がある。
個々の確率が\(D^{-n}\) という形で書ける事。(nは自然数か)
5.2 Kraftの不等式の証明のメモ
勉強会でやるので真面目に読んだ。という事でメモ。
式5.7は、あるシンボルのコードの長さがliとして、その下にlmaxまでの仮想的な足を全部生やすといくつになるか、という風に考える。 これが5.7式のシグマの中。
これを全コードに対してやれば、lmaxの全枝の数よりは小さいはず、というのが5.7の表す事。
5.4まで読んだ
間違った分布にもとづいたコードはKLダイバージェンス分だけ長い、というのは、いかにもそうなりそうな結論が本当になって、なんかすごい事言ってる感じがする。
それにしてもここまで計算が楽なのにこんなに一般的な結論が出まくるのは驚きだねぇ。こんな簡単にこんなタイトなバウンドが求まるのか…
5.55の前の式の不等号は反対かなぁ。 この手の奴は突然脳にめっちゃ負荷が掛かるのよね。
5.6 HUFFMAN CODES
ハフマン符号はアルゴリズムだけ追った事はあるがあまり理屈は理解してなかったので、ちゃんと読む。
マージするツリーがあれば、必ず足は2個ずつに分岐してるので、それが現時点の末尾の0-1に対応する。 あとはルートから順番に降っていけば良い、という事か。 めっさ簡単で感動するな。
5.8 ハフマンコードが最適な証明
MacKayの方の勉強会でこの辺当番になってしまったがこの本の方が分かりやすかったので、ちゃんと証明を追う。
向こうのノートからもリンクを貼りたいので別ページに分けた
5.9 Shanon-Fano-Elias coding
ここまではスラスラ読めたのでメモは無し。 完璧に理解してる訳でも無いが、必要性を思えば十分といえるくらいの理解はあると思う。
で、式5.73のすぐあとが一瞬分からなかったのでメモ。 xはここでは上のギリシャ文字Xの要素で、それらは全て確率が正だとしている(5.72の上参照)。 つまり必ずFの階段の境界。 aとbも同じ。
5章、なかなか面白かった
最後の確率変数をfair coin flipで実装する話はPPLっぽいな、とか思いながら、証明のあらすじだけ眺めて終わりとする。
全体的に説明が単純かつクリアで、面白くて読みやすい内容だった。 ただ自分に要るか?と言われると良くわからないが。 教養としての読み物みたいな感覚だな。
ちゃんと細かく追うよりはこんな感じでサラサラ読むのが正しい読み方と思うし、そう思って接すればなかなか良くかけた章に思う。
情報理論、なかなか応用多くて面白いな。
6章 ギャンブルとデータ圧縮
ギャンブルは計算自体は単純で、結果の戦略もそんなに面白い話では無い。 ただ理論的な上限とかが割と簡単に出て、それがエントロピーとかと関係するのは何かの深淵みたいな物のそばを見ている気にはなる。 情報理論はそういうのが多いな。 別段難しい所は無いのとそんなに興味も高くないので軽く読んで要点の式変形だけ眺める程度で進む。
6.5のデータ圧縮との関係は良くわからない。ベットというのを実現しうる系列がいろいろある時の、ある系列の同時確率である、というのは理解出来る。
その次のcopression algorithmの話が良くわからないのでメモを書いていこう。
まず、01のビットで表された系列を、k桁の01でエンコードする。 xの方はlexicographicalな順番が定義されいる。
で、以下のようなFが定義されている。
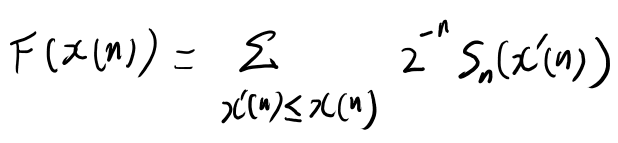
これはxの累積分布関数なのか? いや、これは富の累積分布関数に近い何かか? ちょっと良くわからないな。
まず0から1の範囲に収まる、と言っているので、それを考えてみよう。 x(n)が辞書順で一番最後の時のFを考えてみる。 この時は全xについて、Snの和を取る事になる。
Snとはなんぞや?というと、式6.41や6.42を見直せば、その系列の確率に\(2^n\)を掛けた物になってる。
つまりある系列が実現した時の富だよな。 それを全系列について和を取ると、それは富の期待値になる訳だ。 それは1か?2 for 1だとそうだ、という話だと思うが、、、
良くわからないな。具体例を考えて見よう。
簡単の為、00の確率が9/10としよう。 01, 10, 11の確率が残りを3等分、、、すると割り切れないので、3/100, 3/100, 4/100としよう。
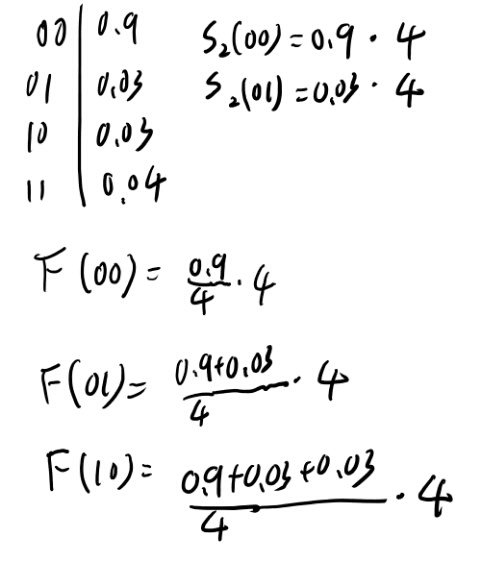
なるほど、Snの定義に\(2^n\)が入ってるので、Fではそれを割るので、本当にbの、というかxの系列の累積分布関数になるんだな。 和は同時確率の和なので当然1となる。 理解した。
で、Fは単調に増加なので、Fの厳密な値を与えれば、その逆像でxの厳密な値が分かる。 ただこれでは必要な桁数は減ってないので、この隣と区別する最小の値である必要がある。
で、これはあるx’を加える前、加えたあと、次の値を加えたあと、の3つを区別できれば良い。 前後の大きさに依存しない為には、このx’で加える値の中である事が確定する桁数であれば良いのか? ちょっと具体例で考えてみよう。

ようするに、最初に0じゃない1がある所までで十分か。
一つの系列に対して、足すものは以下だよな。
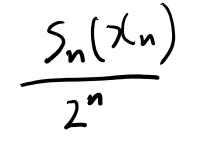
ああ、kはこれのlog2にマイナスをつけた値か。 例えばこれが2.3なら、二桁目まで、、、って切り上げじゃないとだめじゃないか? なんかガウス記号っぽくなってるが。
kが2.3なら、0.xxまで送る、という事になる。 そし足される物は0.001よりは大きい何かな事が保証される。
そして、インターバルの所は誤植があるが、意味を考えると0.xx+1/4以上になった最初の場所、という事か? いや、これだと前の物がすごく小さい時に区別出来ないかな?
どういう誤植なんだろう。
0.xxまで送って、今回足した結果の値である事が分かる必要かある。
例えば0.xxyまで送れば、確実に今回足された値の結果である事は保証される。 これはyの桁は今回の計算で確実に更新されるので、yより上の桁の値だけ一致すれば、それは今回の系列である事が保証出来る。
0.xxまでで区別出来るか? 例えば、足す前が0.1だったとする。
で、0.001001が足されたとする。 0.101001になる。 このうち上2つだけ送ると0.10。 これは一見すると0.1と区別出来ないが、0が送られている、という事から判断出来る事はありそう。
この場合は0.101を最初に越えたら目的の値な事は確定する。
お、なるほど。では繰り上がりでも成り立つか?考えてみよう。
もともとが0.0011だったとしよう。 そこに0.0010001が足されたとする。
足した結果は0.01010001となる。 上2桁という事で0.01が送られる。 この場合は最初に0.01に到達した所が目的となるが、0.011では行き過ぎなので駄目だ。
この両方で成り立つ範囲とはどういう範囲か? うーむ、なんか存在しない気がするな。ちょっと紙版の誤植が無い奴を確認したいなぁ。
まぁいいや。暫定的にkの定義は切り上げの誤植、そしてc(k)を最初にこえたところが目的のxというアルゴリズム、と予想しておこう。
追記: 紙版を持ってる人に聞いた所、やはりkは切り上げらしい。そしてインターバルは以下。
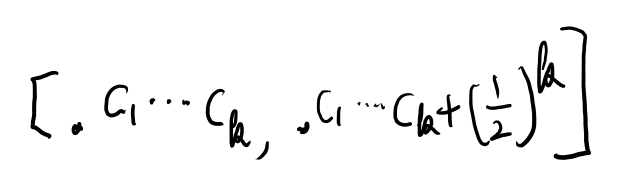
6章読み終わり
何箇所か良くわからない事があったが、全体的には簡単な計算の結果が多い。 結論の戦略自体はそんな驚きも無いが、boundsが出てそれがエントロピーと関係が深いのは面白いね。
あと単純とは言え戦略も、以前金融か投資かなんかの本で似たような結論を読んだ事がある気がするが、ちゃんと理解出来たのは今回が初めてな気がした。 当たり前の結果だけど、当たり前と感じられる度合いは以前より増した気がする。
圧縮との関係も良く書けてるし、なかなかおもしろい章だな、と思った。いい本だね。Kindle版の誤植かもうちょい直ればもっといいのになぁ。
7章 チャンネルキャパシティー
全く興味が無いのでなるべく軽く読みたい。 相互情報量の計算は二章で幾つかやっててるので当時のメモを見直したりするなど。 このブログに残せるようになったのはすごく便利だな。
結局、後半の証明などは追わずに結論だけ理解するに留める。 一応どういう問題設定でどういう定理があるかくらいは眺めたので、似た問題設定の時に気づくくらいは出来るかも。
この本は扱う話題が多様なので、このくらいの読み方の緩急をつける方が良い気がする。
8章 Differential Entropy
エントロピーの連続への拡張の話なのだが、突然実解析的な定義になるのだな。 Distributionからの定式化は去年散々やったのでむしろ得意分野だぜぃ。
support setはうろ覚えなので定義を書いておく。
あるrandom variablbのdensityをfとした時、f(x)>0となるxの集合を、Xのsupport setと呼ぶ。
Dudleyの定義は差の測度がゼロになるような最小の閉包、っぽいけど、だいたいは同じ事か。
8.9式は分母にlog 2 eが必要そうだな。
f(X)について考える
8.2.1ではf(X)という物が出てくるが、これはなんだ?fはdensityなのだから、引数は確率変数では無くてその値域の集合でないとおかしいと思うのだが。
次の8.2ではp(X1, X2,…)みたいなのが出てるが、これはAEPで出てきたとの事なので3章を見直すと、これは観測値の系列の得られる確率という事になってる。 うーん、これはpが小文字なのか?…まぁ妥当性はおいといて意味することはこちらはわかる。
fの方も同じように考えられるか? X1, X2, …は適当にサンプルされた実際の実数値とする。 それらのfの積。 これは定義出来るな。 意味することは相対的な尤度みたいな意味付けは出来るが、確率的には積分してないので何の意味もない値となる。 ただ大きくしていけば、empricalな期待値という事にはなるだろう。
次に- log f(X)の期待値とはどういう事を表してるのだろうか?
例えばE Xは、厳密には以下の定義となる。
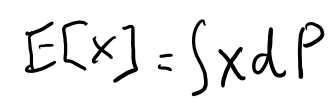
このPによる積分というのはsimple functionでの近似で定義出来るんだよな。 まずは確率空間のノーテーションで全部書き下そう。
まずはsimple functionの定義(Dudleyのp114 4.1.1より)

厳密な事をおいとくと、あるオメガの元wを、それを含むボレル集合族の元をいっぱい集めて 適当なボレル集合族の元ごとに定数を割り振った物の和で表される、という事。
このBは一般のものだが、定理4.1.2によりそれと同じものを必ずdsjointな集合族で書き直せるので、以後はBはdisjointとする。
で、このgの測度Pによる積分は、以下で定義出来る。
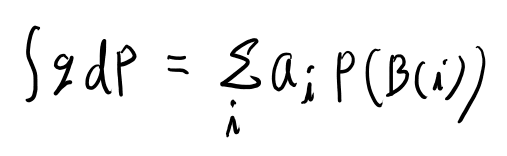
これくらいでもとのf(X)がらみの期待値を考えてみよう。
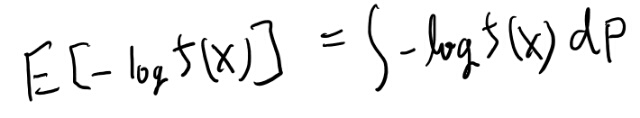
ん?fとXの合成関数になるの?何それ? ちょっと意味が分からないなぁ。
なんか気分的にはこういうのを求めたいと思うのだが、
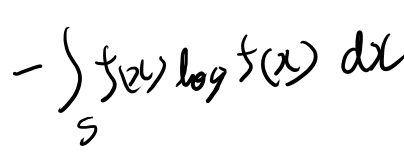
同じになるかしら? うーん、少し考えたが全然分からん。もっと真面目に考えてみよう。
適当な細かdisjointな区間に分割して、それをBと呼ぶ。 Bを使ってXはsimple functionの形で書ける場合を考える(これは任意のXの近似形なので一般性を失わない)。
オメガもあらわに書くと以下のようになる。
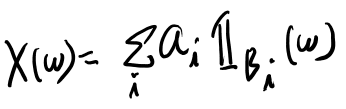
さて、これを用いると、求めたい積分は以下のように和に直せる。
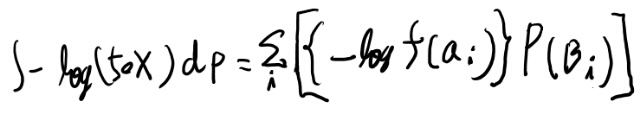
これはさっきの積分、つまりh(X)と同じ物か?
うーん、なんかf(x)が足りてないような? どうなんだろう。分からん…
追記: なんか実数側での積分に直す時にfが出てきそうな気がしてきた。 lawで考え直せばいいか? 考えてみよう。
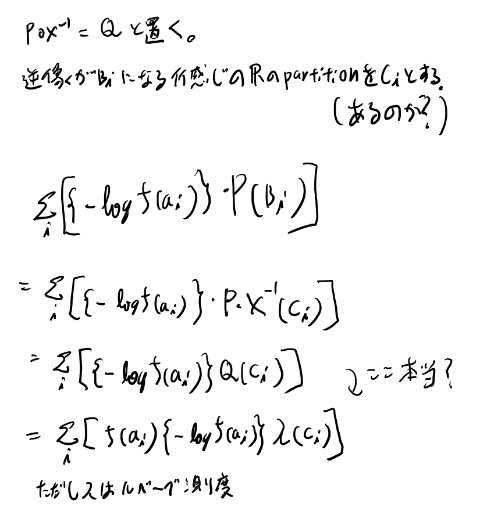
二箇所怪しい所はあるが感覚的には一致しそう。
定理 8.2.2 typical setとその体積の不等式
2の証明で8.11の条件の絶対値の外し方が分からん、と一瞬思ったが、マイナスの時も8.11の条件の、右辺は正で左辺がマイナスなのだから成り立つな。 だから、8.14から8.15の変形はどちらにせよ成立するか。
式8.18から8.19も同様の場合分けが必要で、以下のようにどちらの場合も示せる。
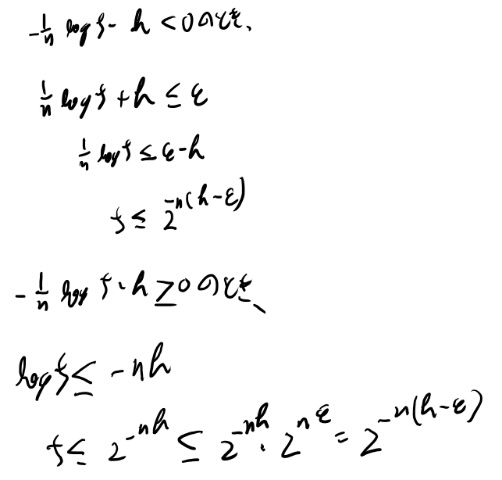
8.3 離散的なエントロピーとDifferential entropyの関係
自分がやってたような計算をリーマン可積な範囲でいろいろやってるので追っておく。
まずそろそろ忘れがちなので8.1のDifferential entropyの定義から。
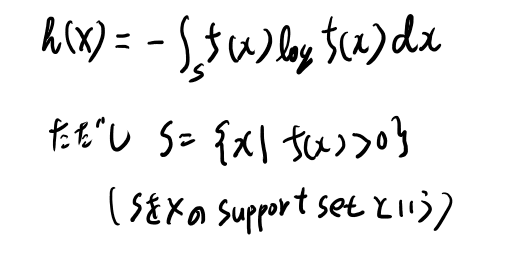
さて、定理8.3.1はいいとして、そのあとの記述、h(X)+nがどこから出たのかを考える。
8.30式の右辺はh(f)とかいう未定義な物が出てきてるしわかりにくいが、無視してh(X)に収束する、と思えば良さそう。 それは8.29式の帰結。
8.30を近似として、書いて移行してみよう。
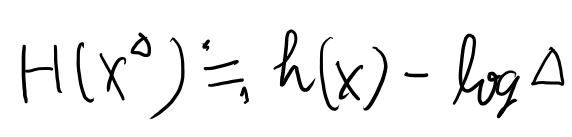
n bit quantizationとは、2の-n乗で分割するという事か。 ではlogのデルタは-nになるのね。理解した。
Example 8.3.1を計算してみる
次にExample 8.3.1の計算をしていく。 1のhが0は良く分からなかったが、Hの方は暗算で出る。
次に2。これはf(x)は定数で8という事だよな。 という事はh(X)は以下。
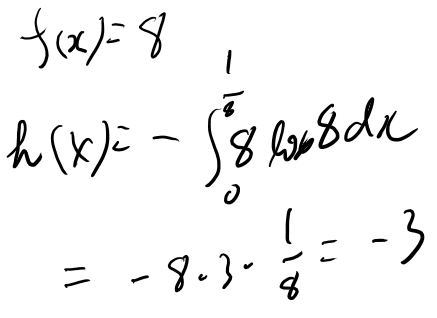
3は8.1の最後のexampleとほとんど同じ計算なのでメモは残さない(一応やってみたが)
8章はなかなか面白かった
8章は読む前はただの連続にしただけ、という話だと思ったら、意外とちゃんと離散的な所からの極限として扱うという話だったので、離散的な場合の理解と割と深まった。 一方で雑なdensityの扱いはたまについていけなくなる所もあって、結局実解析の復習をするハメになったりした。
この辺はうまい事古典的な感覚で押し通せる方が理解は早いと思うのだが、中途半端に極限とかを議論するので辛いのだよなぁ。
なかなか興味ある章なので計算を追おうと思ったが、結構解説自体が詳細なのであまり手を動かさなくても追えてしまった。
細かい定理を全部マスターしたという訳じゃないが、必要になる都度戻ればいいかな。
九章以降につづく。