Elements of Information Theoryの一章、二章
Elements of Information Theoryの読書記録
そろそろ情報理論を真面目にやるか、と決意して、以下の本を読み始める。
amazon: Elements of Information Theory (English Edition)
これはGoodfellow本から参照されてた二冊の本のうちの一つで、サイコロ本でも確か言及されてて、Kindle版があった、みたいな基準で選んだ。
1.1 Mutual Informationの計算
Example 1.1.3とかをやっておく。 まず必要な事を簡単にメモ。
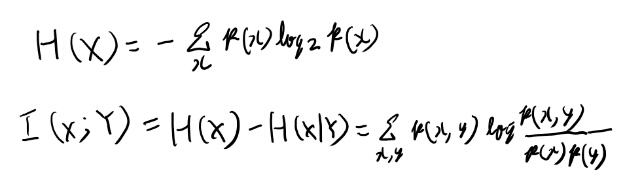
最後の式は簡単に確認しておくか。
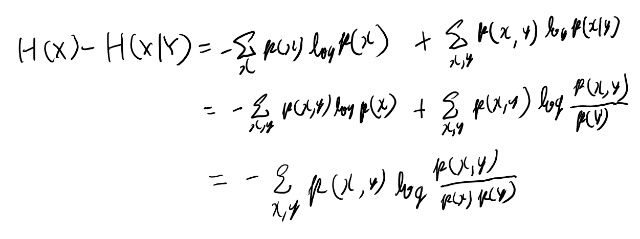
conditional entropyは式2.10に定義がある。 条件付き確率の期待値なので同時分布の和になる。
ノイズなしバイナリチャンネル(Ex 1.1.3)
information capacityは1ビットとなる、と言ってるが、定義に従い計算してみよう。
まず、xが0か1を等確率で送る場合の計算をしてみる。
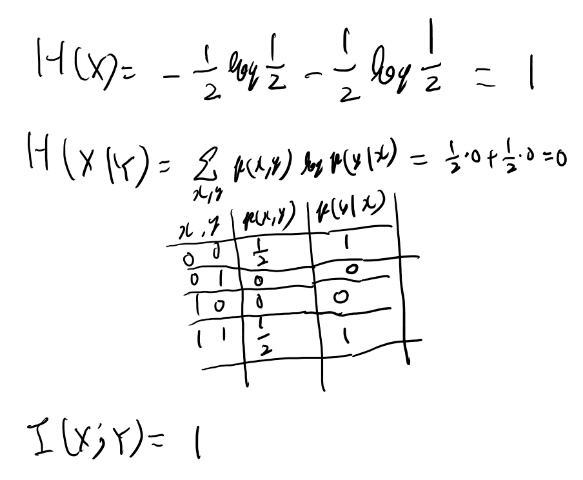
結局p(x|y)はいつも1か0で、0の時は同時確率がゼロだから寄与しない。 という事でいつもxのエントロピーと一致するのか。
ではエントロピーが最大になるxは?という事になり、これは変分法で凸関数がどうとかになる話と思うが、離散的な上くらいの例なら1となる確率をp、0となる確率を1-pとしてpで微分、とかで出そう。 実際p(1-p)はpが1/2の時最大だろう。
(追記: Example 2.1.1に解説があった)
なるほど、xの分布を変えて最大値を狙う、というのがinformation capacityという概念か。
バイナリ対称チャンネル(ex 1.1.5)
これも計算してみよう。xは等確率で0か1で良かろう。 とりあえず必要な表を書く。
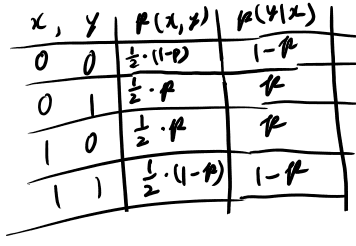
なるほど。これを使って定義に従って計算してみる。
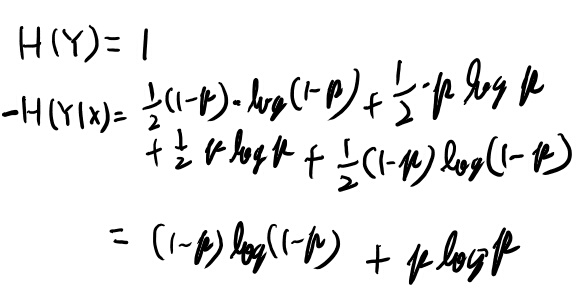
なりそうだね。
2.2 conditional entropy
2.1は特に分からない事は無かったのでさらさら読む。 2.2のconditional entropyはちょっとメモを残したくなったのでメモ。
conditional entropyを考える時、条件付き確率は、古典的にはなんらかのXの実現値に対して定義される。 なので、\(H(Y| X=x)\)は自然に定義出来るが、これのXでの期待値が\(H(Y| X)\)の定義になる。
すると式2.10からの一連の変形で2.12のように定義される。 一応自分でも確認しておこう。
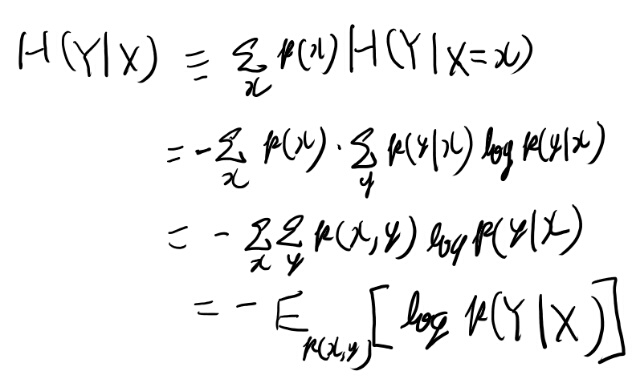
実解析でちゃんと扱えば集合論的に出せそうな結論だが、ゆとりなのでそういうのはしない。
一応チェインルールもメモしておこう。
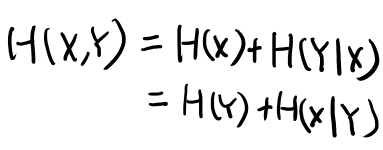
Example 2.2.1 Conditional entropyを手計算してみる
やってみよう。
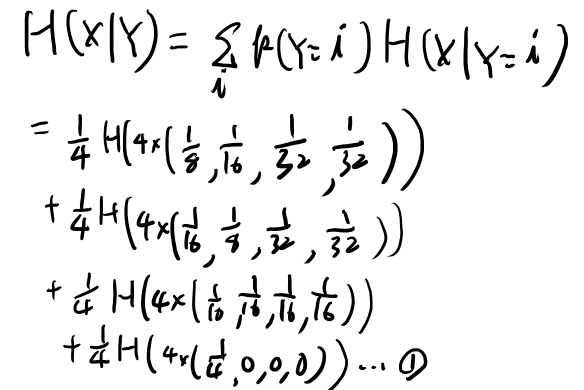
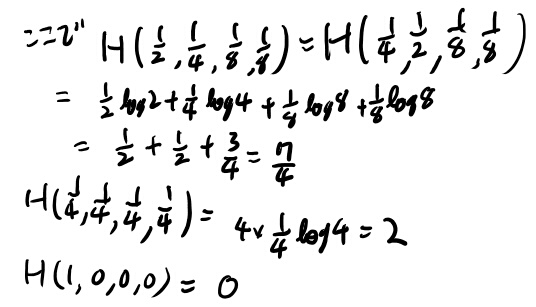
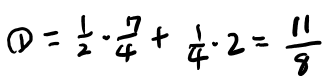
ちょっと慣れてきた。こういう問題解くって大切だよなぁ。
mutual informationとKLダイバージェンス
relative entropyはKLダイバージェンスの事。定義はまぁいいだろう。
mutual informationは、同時分布とマージナルの積のKLダイバージェンスで定義は以下。
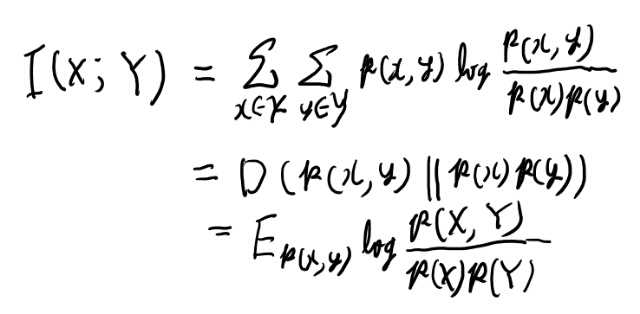
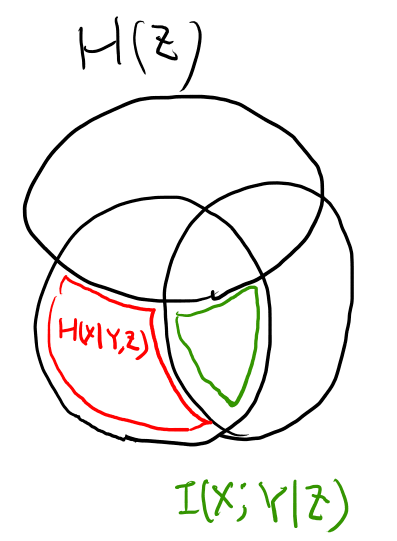
図2.2はなかなかわかりやすいのでメモしておく。
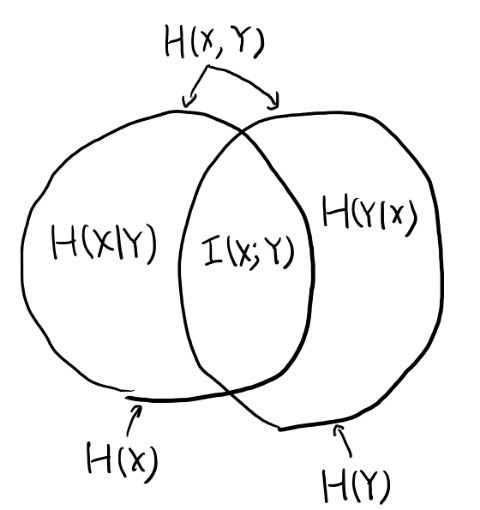
次のConditronal mutual informationもこの図で考えるとわかりやすいな。
conditionalなrelative entropyが2.65で出てくるが、ちょっと積分対象が予想外なのでメモしておく。
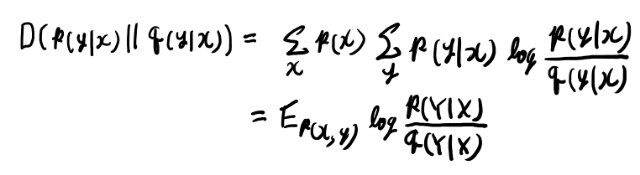
p(x)での和が入るのが、直感的には分かりにくい所だな。xの側もボレル集合族の集合にしたいと思えば自然なのだが。
ところで条件付きrelative entropyは条件付きKLダイバージェンスって呼ぶのかね? あんま聞かないが。
KLダイバージェンスがconvexとは
定理2.7.2でさらりと定義が書いてあるがあまり知らない概念なのでメモしておく。
KLダイバージェンスがconvexである、とは、\(( { p_1}, { q_1})\)と\(( { p_2}, { q_2})\)がもし2つのペアのprobability mass functionなら、
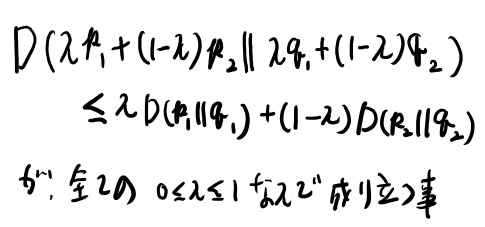
なかなか難しいが、pとqを無限次元のベクトルと思えば、p1, q1とp2, q2の間の点について述べていると思えば通常のconvexの定義と等しい。 なかなかヒルベルト空間だな…
なおこれは成り立ってるのでconvexとの事。
Mutual informationがconcave(定理 2.7.4)
Mutual informationがp(y│x)を固定するとp(x)についてconcave、またp(x)を固定するとp(y│x)についてconcaveとの事。
汎関数のconcaveについて良い練習になってそうなので計算を追ってみる。
まず前半。条件付き確率を固定すると、p(y)はp(x)のlinear functionだと言ってる。 どういう意味だろう?
まずp(y│x)を固定と言っても定数という訳じゃない。だからp(y)はp(x)の定数倍という訳じゃない(そもそも積分したら1なので定数倍はありえない)。 だからヒルベルトスペース上での話をしてるんだろうなぁ。
良く分からないので、H(Y)がconcaveかを定義に従って見てみよう。 まずLog sum不等式を書いておく。(定理2.7.1)
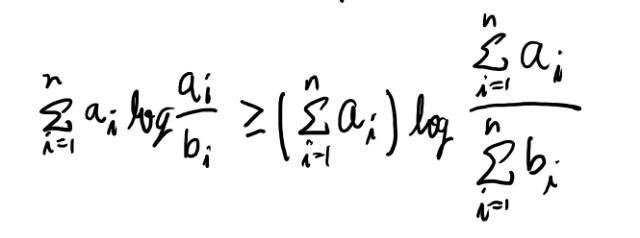
これをつかってKLダイバージェンスがconcaveなのが示せるらしい(定理2.7.2)
そして一様分布とのKLダイバージェンスと合わせて考えてEntropyがconcaveなのが示せるとか。
それを使ってこのmutual informationについての定理2.7.4が示せるらしい。 やってみよう。
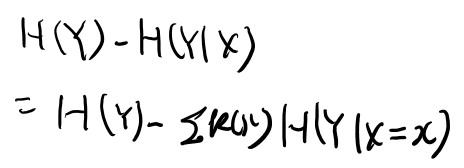
p(y│x)を固定するとp(x)についてconcave
まずはp(y│x)を固定する方を考えてみる。 この時p(x)についてconcaveとは?
解説にはp(y)がp(x)のlinear functionになる、と書いてあるが、さっぱり意味が分からない。p(y│x)は固定するとは言っているが関数なのでは?
こういうのはちゃんと定義に従って書いていくのが良さそう。 まずp(y│x)を固定してp(y)との関係を考えるのだから、同時分布をマージナライズすれば良かろう。
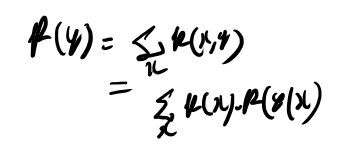
さて、p(x)についてconcave、というのは、p1とp2の2つの関数についての概念だよな。
まずp(y)についてエントロピーがconcaveなのは前に証明してあるので、これを使おうとしてみよう。 Yのエントロピーの、concaveの定義の式の左辺を書いて変形していってみる。
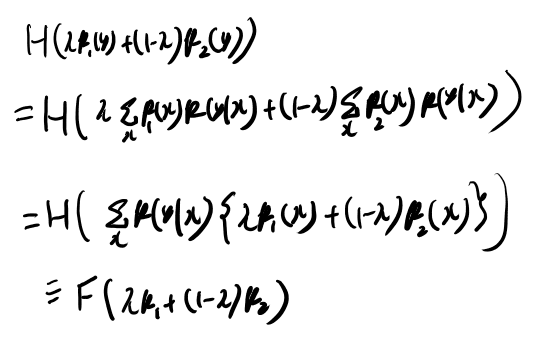
最初はマージナライズして消えちゃうじゃん、と思ってたが、それが関数に依存する値になるので、一歩引いて考えればそれは何らかの汎関数なんだよな。 それをFと置いてみると、これはqの汎関数になってる。
右辺も同様に変形してみよう。
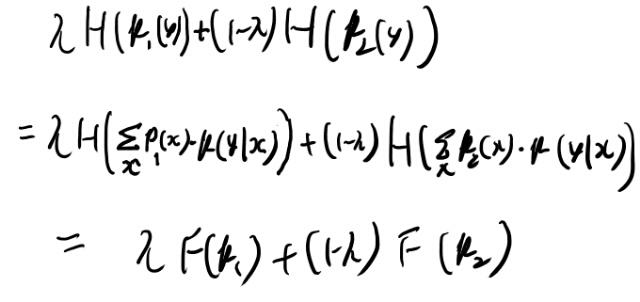
これはp(x)についてconcaveだ。なるほど。こういう事か。
さて、第二項のHの方はもともとp(x)には依存してない。 で、p(x)に固定の関数を掛けて和を取った物になっている。
これは、
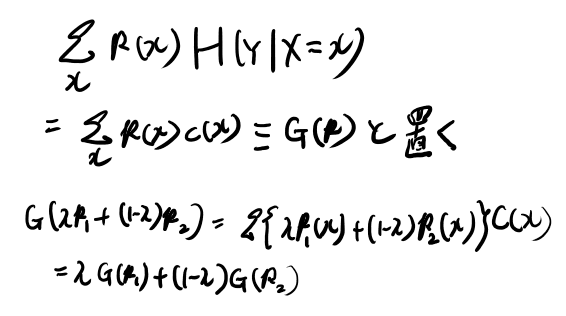
なるほど。線型変換は足しても引いてもcovexityに影響は与え無さそうだな。納得した。
p(x)を固定するとp(y│x)についてconcave
次に、p(x)をfixedにすると、p(y│x)に関してconcaveになる、という話。 これの証明が良い勉強になりそうなのでこちらも追ってみる。
まず前と同様に同時確率に結びつけたりxに関してマージナライズしたりしてみよう。
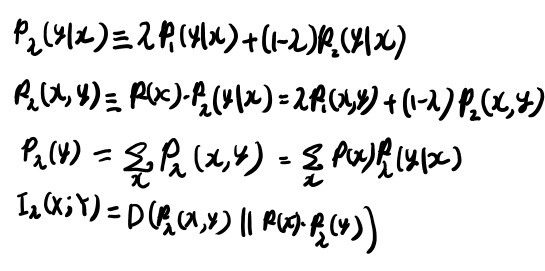
ここから解説ではDがconvexだから、と言って終わってるが、いまいちなにを示したのかがついていけてない。
定義に従い、右辺も書いてみよう。
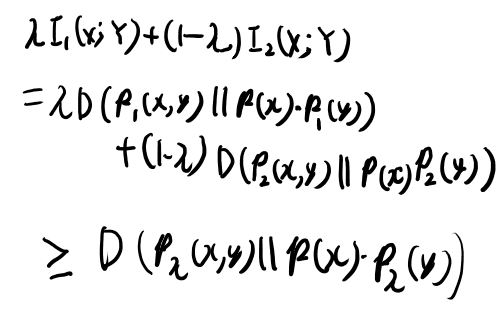
ここまでは良い。この事実から、p(y│x)のconvexityにつなげたい。
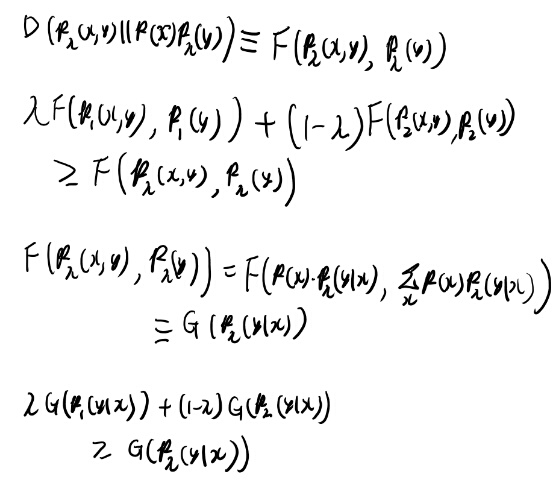
言えた。具体的な計算は一切行って無いのだから当たり前のはずだが、何が当たり前かいまいち分からないな。
何かの汎関数がconcaveで、その引数の関数の内分点が、おなじ比率の別の何かの関数の内分点によって完全に決まるなら、この別の何かの関数に対してもconcave だ、という事を言ってる気がする。
この内分点がうんぬん、というのは、きっと線形変換と等価になる、、、のか?ちょっと自信は持てないが。
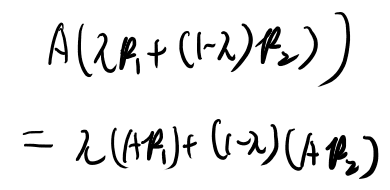
これは線形変換だな。 一般のバナッハ空間に対しての線形変換はそんなにちゃんとは理解できてないが、たぶん言えそう。
2.8 Data processing inequality
めっさマルコフ確率場の話から始まる。 こういうのって別の所で学んだ事無いと厳しいよなぁ。いわゆるPGMという奴ですね。
この矢印は一次元のベイジアンネットワークのような気もするが。
定理2.8.1 Xー>Yー>Zなら、I(X; Y) >= I(X; Z)
感覚的には、Zまで行っちゃうと何かの情報は失われてるからこうなる、という話な気はする。
YがgivenだとXと独立、というのは、エントロピーのベン図としては、XとZが重なる所は必ずYの中、という事だよな。 図にするとこんな感じか?
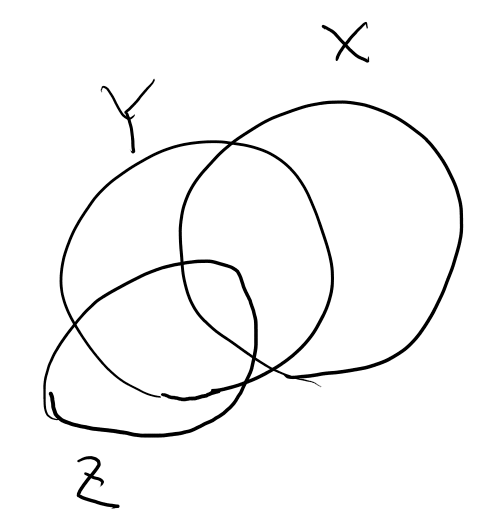
定理が述べてるのは、XとYの交差の部分は、XとZの交差の部分よりも大きい、と言っている。 必ず交差の部分はYに含まれるのだから当然。 これをまじめに示す、という話だな。
式2.119と2.120で出てくる要素を書き込んでみよう。
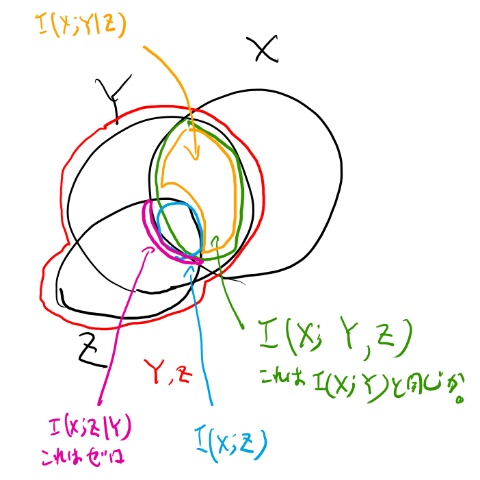
図からはほぼ自明だが、図をそういう風に描いてるからでもある。
黄土色と水色を足したら緑になって、緑がI(X; Y)だと言えば良さそう。
証明を眺めると、まずI(X; Y, Z)を2つの方法で分割する。 この分割は図的にはほぼ自明なので良かろう。
次に、I(X; Z│Y)を示す所でマルコフ性を使う。 ここだけ言えばまぁ良かろう。 これをちゃんと定義に従って書いてみよう。
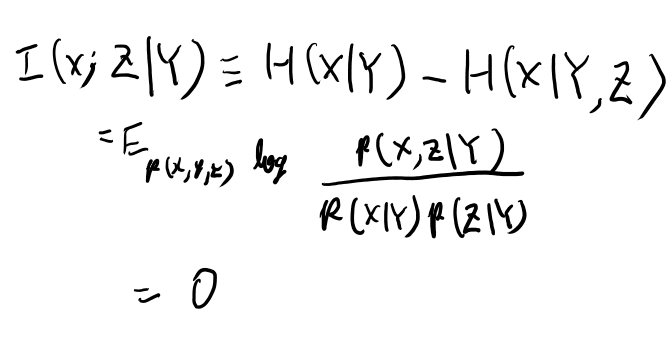
言えそう。他はまぁ良かろう。
2.9 十分統計量
十分統計量のちゃんとした定義とか、なぜそれを十分統計量と呼ぶのかが分かる。 へー。
ここから突然Xがサンプルになるのがすごく分かりにくい。勘弁してよ…
で、定義は \(f_\theta(x)\) をprobability mass functionとする分布からXというサンプルを取り出す(つまりこれは集合か)。
で、このサンプルに対しての統計量がT(X)として表される時に、T(X)をgivenとするとXとシータが条件付き独立になるとき、T(X)を十分統計量という。
これは以下の等式と同じと言っている。
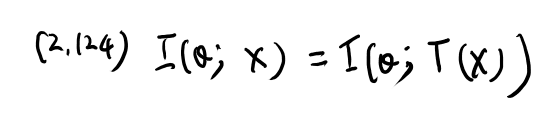
これはまた全然分からん式が出てきたな。 まずXはexampleと言ってる。 それではそのexampleとの相互情報量とはどう定義されるのか?
やはりXは確率変数じゃないとおかしいよな。 どういう確率変数かというと、n回サンプリングした時のn個のxを各次元に持つベクトル、という確率変数なんだろうな。
これでXは確率分布するし、その上の統計量としての関数も定義出来る。
これを自分で考えないといけないって厳しい教科書だなぁ。これなら素直に測度論の言葉でちゃんと書いてくれる方がずっと簡単だ…
まぁいい。Xはそんな意味でのn次元の確率変数だ。
シータが確率分布してるというのは意味が分からないが、不確かさを確率分布と考えるのだろうか。 何か値は分からない。だか何かの値からXはサンプルされたと考える。 この不確かさを分布とするのはベイズ的にはそういう物かもしれない。ただXもそこからサンプルされる、というのが珍しいパターンだな。
例2. 分散1の正規分布の十分統計量が平均という話
この例2は少し分かりにくい。 例えばXの平均を100としよう。
これがどれくらい出にくいかは当然シータの値によって変わる。 シータが10くらいならあまり起こりそうも無いし、シータが99なら良くありそうだ。
一方であるサンプル平均がgivenとすると、その条件を満たすXの分布はシータには依存しないのか? 良く分からない。
表記の都合で平均をMとして、対数尤度をがちゃがちゃしてみよう。
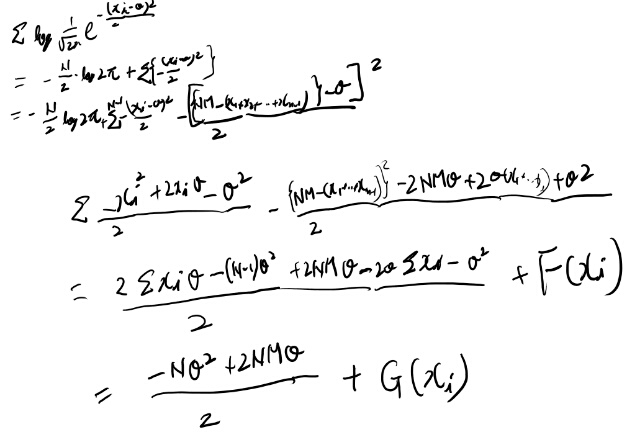
シータは消えないが、別の項に分離された。 これっていいのだろうか?
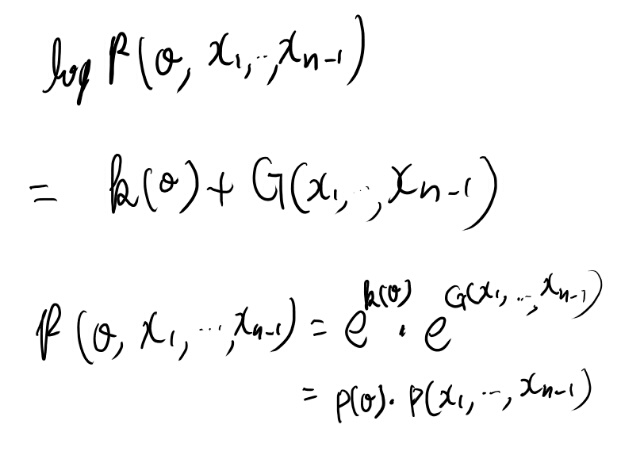
条件付き独立と言えてる気はする。 つまりMをgivenとすれば、相互情報量はゼロか。
なんかスッキリ分かった感じはしないが、証明は出来てしまった。 この辺ちゃんと理解してる人に教えてもらいたいなぁ。
2.10 Fanoの不等式
ある確率変数Yを知った上で、別の確率変数Xについて推測したい、という時の話。
冒頭に問2.5の Zero conditional entropyの結果を発展させて考えてるので、この問題をまず解いてみよう。
問2.5 Zero conditional entropyの帰結
H(Y│X)=0なら、YはXの関数だ、という事を証明する。 関数であるとは、for all x with p(x) >0に対し、p(x, y) >0となるyはただ一つ、との事。
ふむ、全然分からん。定義に戻って式をガチャガチャしてみよう。
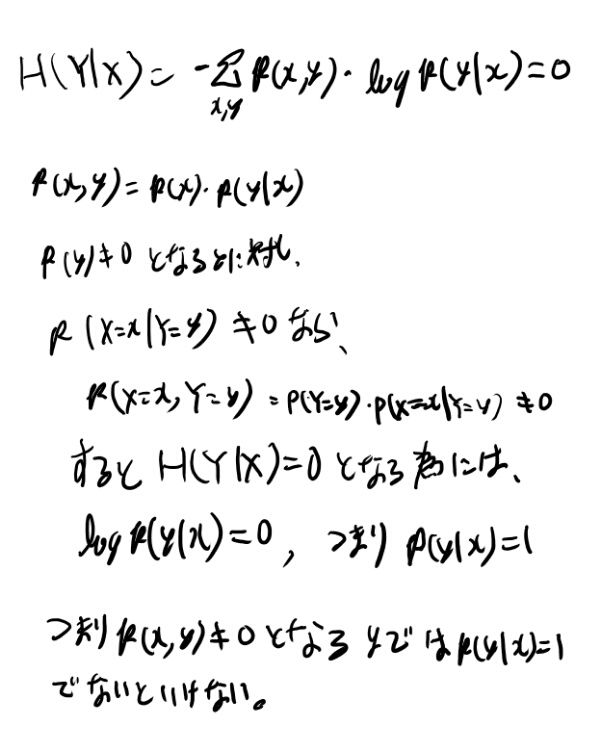
なんか偶然証明出来てしまった…
p(x, y)が’0でないようなyが一つあるとすると、xによる条件付き確率が1になる、つまり関数になってる事が示せる。
一つは存在するのは確率空間である事から明らかか。
Fanoの不等式
確率変数Xをpredictしたい。 観測は確率変数Y。 XとYが普通の機械学習と逆なので注意。
で、p(y│x)は分かってるとする。 一つしか無いHMMみたいなものか。
ここからギリシャ文字が多くてメモが難しいな。 教科書を参照する事を前提に書くか。
ハットでestimatorを表すとすると、Fanoの不等式は以下のように書ける。
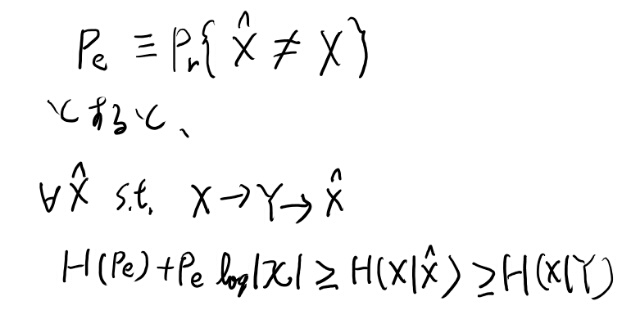
証明の所の式2.134を図で描く。
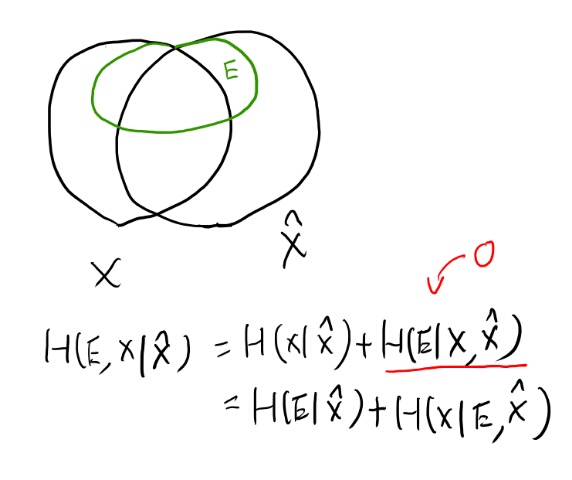
だいたい明らかだな。で、この最後の式の項がそれぞれ不等式で抑えられるらしい。
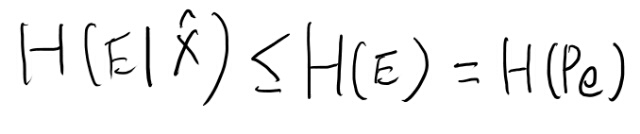
最初の不等式は自明として、後者は難しい事言うな。 ここまで来ると測度論の言葉無しでは何を言ってるかが分からん。諦めてDudleyを見直しながら考えよう。
H(E)とは何か。 densityをf_Eと書くとすると、このf_Eで定義されたエントロピーだよなぁ。
これとPeのエントロピーは等しい? とりあえずH(E)から考えよう。
p.284によると、densityはPのラドンニコディム微分が定義なので、、、ってPはlawだよな。 lawってなんだっけ? ああ、下の確率測度とXの逆像の合成、つまりX上の確率測度みたいなもんか(いい加減な言い方だ…)
このf_Eの、f_E log f_Eの期待値がH(E)だよな。
次にH(Pe)を考える。 Peとは何かというと、P(E)の事だよな。 つまり、、、Eのlawか? densityはそれのラドンニコディム微分なので、、、あれ?f_Eと一緒な気がするな。
たぶんH(Pe)って未定義な概念だよなぁ。 エントロピーはlawに対する概念じゃなくてランダム変数に対する概念だよな。 それともPeを確率変数と考える事ができるのか?
あるボレル集合族の元、つまりあるeventについて考える。 Peは何かの値になるな。 逆像は考えられるか? 例えばPeが0.1の時、そのeventを考える事はできるか?
XとXハットの同時分布というか、像の範囲は決められそうだな(連続なら無限にあるが)
うーむ、なんかPeが確率分布する、と考えられるか良く分からないな。PeはXとXハットの値域が一致してる、というシグマ集合族に関する測度の値な訳で。 それは確率変数とは違うんじゃないか。
Eは確率変数だろうが、Peは違う気がする。
やっぱりH(Pe)は未定義な概念じゃないか。
Pe log Pe の値は定義出来るよな。 これを積分出来るか? 何に対して積分するのだろう?
普通期待値ってXに対して定義される概念なので、これを積分する対象はやはり謎だな。 これは未定義概念なんじゃないか。
むしろ式2.130自体が、H(E)の間違いなんじゃないか。Wikipediaを見ると、H(e)と書いてある。 このeはimplicitに定義されてるが、これはEと同じだろう。こちらの方が理解出来るな。
その後も同様にpについてのエントロピーが出てくるが、これは未定義だよなぁ。 pの表すランダム変数のエントロピーの事、と思って読み進めるか(めちゃくちゃややこしいが…)
気を取り直して。定理2.6.4で、entropyのupper boundが以下になる事が示されているので、これを使う。
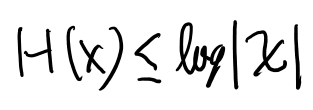
証明は一様分布とのKLダイバージェンスを考える。
これでFanoの不等式の1つ目の不等式は示せる。 2つ目は前にやったData procesing不等式から出せるとの事。確かに出せそう。
2章読み終わり
2章はとても良い勉強になった。
自分はエントロピーとか相互情報量とか、何かのついでに軽く書かれた物で読んだ事くらいしか無かったので、こうやって本格的に学んだ事は無かった。
ちゃんとやると当然だが理解が深まるし、とても重要な概念なので理解が深まるのは非常に良い事だと思った。 解説中に簡単な練習問題がたくさんあるので、習うより慣れろでとりあえず式変形していく事でいろいろ慣れる事が出来る。 やはりこういうのは計算して慣れるのが一番だよね。
全体的に汎関数とか測度論を表に出さずに簡単に解説するが、KLダイバージェンスの凸性とかはバナッハ空間で考えないと意味が分からないし、エントロピーやKLダイバージェンスが汎関数という理解が無いと途中でさっぱり分からなくなると思った、というか自分はなった。
ただどういう数学を使うかはおいといて、このエントロピーや相互情報量をしっかりやるのは良い訓練になる。 これは必要な事だなぁ。
最後のFanoの不等式の所は、 確率変数とdensityを、たぶん意図的に曖昧に書いてる。 すんなり納得できてる間は難しい事を考えずに概要だけ分かって良いのだが、ひとたび詰まると辛い。
何かが分からなくて、本当は何を意味してるのかを考えると、凄くややこしかったり、そもそも記述が間違ってたりする。 そうした事を自分で突き止める為にはかなり測度論の基礎から追い直さないといけないので、これなら普通に測度論の言葉で書いてくれた方がずっと自分には簡単だったな…と思った。 ただそのかえって難しいおかげで、良い実解析の復習にはなった。
全体的に、扱ってる内容は素晴らしいので、多少説明が合わなくても本の価値は損なわない気がする。 もっとわかりやすい説明の本があればそれを読みたいが、これまで立ち読みした範囲ではこれだけちゃんとこの辺扱ってる本は他に見ないので、やはりこの本がオススメという事になりそう。 USのAmazonレビュー見てもこの辺は賛否両論ね。
自分はとても勉強になったし、面白かった。
章の最後の1ページまとめが良く書けてる。これは素晴らしい。
追記: twitterで @belowthewaste1 さんから、H(Pe)は例2.1.1の2.5式が定義だと教えてもらいました。ありがとうございます。
例の中で新たな記号の定義を行っている、というのを見落としてた為みなおしても見つからなかった模様(そりゃ無いよ…)
このH(p)の定義もすごくて、このpはベルヌーイ分布のpなので単なる実数となる。 で、H(p)は -p log p - (1-p) log (1-p)という定義となっていて、単純なpの関数となっている。
ふつうに考えたらdensityの時にはその確率変数のエントロピーと定義される、みたいな物かと思っていたし、たぶんそうなのだと思うが、ここでの定義はそういう解説は一切なく単にベルヌーイ分布の時にこの関数をそう定義しているだけの模様。
この事を元にH(Pe)を考えると、PeはまさにこのEのベルヌーイ分布のpと同じ物となるので、H(E)と同じ物となる。
この時点ではわざわざこんなピンポイントな関数を定義した理由は分からないけれど、あとの方できっと使うんだろう、と予想。
こういう、意味的に似てるが結構違う物を混同させるようにこそっと定義するのはきついなぁ… 単純なケースしか出て来ない事を祈る。 ただこの本はその辺ゆるいくせに意外と難しい事挟むんだよなぁ。
ただ難しく考えないで乗り切れるなら乗り切りたいので、難しく考え過ぎずに進めたい。気楽に読み進めてみよう。
さらに追記。 一晩経って、Eに関してのHが、Peの値でどう変わるか、という事に興味があるので、EのHをPeの関数として見る、という事なのだな、と理解。 Peのエントロピーではなくて、EのエントロピーがPeにどう依存するか、と考えるのがポイントか。
第三章以降に続く。