ハーフトーン
ハーフトーン
Stipplingを調べていて、ハーフトーンの方がMFGで作れそうだな、と思い、関連ページを作る。
MdImgrのテンプレート
リンク集
- Halftone shadertoyにあった実装
- Bayer Dithering - Spencer Szabados Bayer Dither
- Dithering part three – real world 2D quantization dithering - Bart Wronski bluenoiseとかinterleaved gradient noiseとか
MFGでの実装
MFGで実装してみる。
単にグレーの濃度を白黒の頻度で表すフィルタを作ってみる
Stipplingとは違うが、単に2値トーン化として雑にランダムにサンプルするコードを作ってみるとどうだろう? ようするに単なるハーフトーンの雑な実装だが。
def result_u8 |x, y| {
let gray = grayT(x, y)
ifel(rand() < gray, u8[0xff, 0xff, 0xff, 0xff], u8[0, 0, 0, 0xff])
}

けっこういいけど、これ、なんかガンマ補正してない時の暗くなるのと同じ結果に見えるな。 アルファをガンマ補正するのはどうなんだ問題と同じでしないのが正しい気もするけれど、 あえてやってみるとどうなるだろう?
def result_u8 |x, y| {
let lgray = grayT(x, y)
let gray = linear2gamma(lgray)
ifel(rand() < gray, u8[0xff, 0xff, 0xff, 0xff], u8[0, 0, 0, 0xff])
}

やはりこっちの方が正しい気はするな。
拡大するとランダムさがトーンとして汚いので、やはりbluenoiseの方が良さそうではある。
ちょっとハーフトーンは面白そうだな。論文を調べてみてあとでページを分けよう。
shadertoyの実装を移植してみる
shadertoyでハーフトーンで眺めていて見つけた以下を移植してみる。
最初は理解せずに書いたが、理解してみるとcosの周期パターンにすぎない事に気づく。sindとかcosdはいらなかったな。
@param_f32 threshold(SLIDER, label="閾値", init=0.6, min=0.0, max=1.0)
let PI = 3.1415926
let PI180 = PI / 180.0
fn sind |a:f32| { sin(a*PI180) }
fn cosd |a: f32| { cos(a*PI180) }
fn added |sh: f32v2, sa:f32, ca:f32, c:f32v2, d:f32 | {
0.5 + 0.25 * cos((sh.x * sa + sh.y * ca + c.x) * d) + 0.25 * cos((sh.x * ca - sh.y * sa + c.y) * d)
}
def result_u8 |x, y| {
let dstCoord = f32([x, y])/input_u8.extent(0)
let rotationCenter = [0.5, 0.5]
let shift = dstCoord - rotationCenter
let dotSize = 3.0
let angle = 45.0
let rasterPattern = added(shift, sind(angle), cosd(angle), rotationCenter, PI / dotSize * 680.0)
let srcPixel = input_u8(x, y)
let avg = to_xyza(srcPixel).y
let gray = (rasterPattern * threshold + avg - threshold) / (1.0 - threshold)
# check raster pattern
# let gray = rasterPattern
[*vec3(gray), 1.0] |> lbgra_to_u8color(...)
}
結果は以下。

おお、結構いい感じだな。
Bayerディザー
shadertoyのブレンディング式はどこから来ているのかなぁ、と調べていて、以下のブログに行き当たる。
Bayer Dithering - Spencer Szabados
ここからどうやって探したのか思い出せないが、以下と同じtxtファイルのinternet archiveを参照しているページがあって、そこからDHALF.txtを読んだ。
という事でこれを単純に実装してみる。
# bayer pattern
def pattern by
[
[ 0.0, 32.0, 8.0, 40.0, 2.0, 34.0, 10.0, 42.0],
[48.0, 16.0, 56.0, 24.0, 50.0, 18.0, 58.0, 26.0],
[12.0, 44.0, 4.0, 36.0, 14.0, 46.0, 6.0, 38.0],
[60.0, 28.0, 52.0, 20.0, 62.0, 30.0, 54.0, 22.0],
[ 3.0, 35.0, 11.0, 43.0, 1.0, 33.0, 9.0, 41.0],
[51.0, 19.0, 59.0, 27.0, 49.0, 17.0, 57.0, 25.0],
[15.0, 47.0, 7.0, 39.0, 13.0, 45.0, 5.0, 37.0],
[63.0, 31.0, 55.0, 23.0, 61.0, 29.0, 53.0, 21.0]
]
let PATTERN_WIDTH = pattern.extent(0)
let PAT_MAX = f32(PATTERN_WIDTH^2-1)
def result_u8 |x, y| {
let pxy = [x, y]%PATTERN_WIDTH
let pval = pattern(*pxy)/PAT_MAX
let level = input_u8(x, y) |> to_xyza(...).y
let gray = ifel(level > pval, 1.0, 0.0)
[*vec3(gray), 1.0] |> lbgra_to_u8color(...)
}
超簡単。
適用した結果が以下。単なるグレースケールに見える。

でもアップにすると白黒2値だという事がわかる。

あまりにもグレースケールっぽくて面白さはなくなってしまうな。
カラー版もやってみよう。グローバル変数やパターンは白黒と一緒。
def result_u8 |x, y| {
let pxy = [x, y]%PATTERN_WIDTH
let pval = pattern(*pxy)/PAT_MAX
let lbgra = input_u8(x, y) |> to_lbgra(...)
let lbgr_q = ifel(lbgra.xyz > pval , vec3(1.0), vec3(0.0))
[*lbgr_q, lbgra.w] |> lbgra_to_u8color(...)
}
これも簡単。 結果は以下。

なんか暗くなっちゃうな。このBayerパターンはガンマ補正の具合がいまいちなのではないか?
拡大すると以下。

昔のパソコンみたい。
ブルーノイズでサンプリング
ブルーノイズのテクスチャで単純にサンプリングする、というのも試してみよう。 と軽くPythonのvoid and clusterのコードで作ってみたが、512x512で2時間も掛かった…ちょっと1024x1024は作れないな。
とりあえず512x512でいいでしょう。 256x256をBGRAに4面パックする感じにしておく。
def bluenoise by load("bluenoise512_packed.png")
let T_SIZE=bluenoise.extent(0)
let B_SIZE=T_SIZE*2
def result_u8 |x, y| {
let txy = [x, y]%B_SIZE
let pxy = txy%T_SIZE
let packed = bluenoise(*pxy)
let chxy = txy/T_SIZE # 0または1
let ch = chxy.y*2+chxy.x #0〜3
let gray = ifel(ch == 0, packed.x, ...)
elif(ch == 1, packed.y, ...)
elif(ch == 2, packed.z, packed.w)
# u8[*vec3(gray), 255]
let level = input_u8(x, y) |> to_xyza(...).y
ifel (f32(gray)/255.0 < level,
u8(vec4(255)), u8[*vec3(0), 255]
)
}
まぁこんな感じで。

割と綺麗ではある。アップにすると512x512の境界が意外と目立ってしまうが。
写真に使うと良く論文とかにある感じになって良いね。

なかなか勉強にはなる。
Interleaved gradient noiseでサンプリング
bluenoiseはちょっと手間なので代わりは無いかな、と探していたら、Interleaved gradient noiseというのが勧められていた。
Dithering part three – real world 2D quantization dithering - Bart Wronski
試してみよう。
上記ブログの式は良く意味が分からないのでオリジナルのスライドを見ると、以下の式が書いてある。
float3 magic = float3( 0.06711056, 0.00583715, 52.9829189 );
return -scale + 2.0 * scale * frac( magic.z * frac( dot( sv_position, magic.xy ) ) );
ふむふむ。scaleは良くわからんがこんな感じか?
def result_u8 |x, y| {
let scale = 1.0
let magic = [0.06711056, 0.00583715, 52.9829189]
let fxy = f32([x, y])
let gray = -scale + 2.0*scale*fract(magic.z*fract(dot(fxy, magic.xy)))
[*vec3(gray), 1.0] |> lbgra_to_u8color(...)
}
結果は以下。

それっぽいノイズになったな。 サンプルしてみよう。

悪くないな。写真でも試してみよう。

なんか写真は白いな。いまいち。
循環パターンいろいろ
ordered ditherは循環パターンと適当に補完すると面白い効果が出る、という事の一種に思う。 そこで循環パターンをいろいろ考える。
sincosパターン
shadertoyにあったコードはいろいろ複雑だが、結局整理すると単なるsinとcosの循環パターンと同じになる(オフセットが違うが)
let PI = 3.1415926
fn sincos_pat |sh: f32v2, pscale:f32 | {
let dir = [cos(PI/4.0), sin(PI/4.0)]
let ortho = [dir.y, -dir.x]
0.5 + 0.25 * cos(dot(sh, dir) * pscale) + 0.25 * cos(dot(sh, ortho) * pscale)
}
def result_u8 |x, y| {
let dstCoord = f32([x, y])/input_u8.extent(0)
let dotSize = 6.0
let pscale = 2.0*PI / dotSize * 680.0
let gray = sincos_pat(dstCoord, pscale)
[*vec3(gray), 1.0] |> lbgra_to_u8color(...)
}
パターンとしては0.0から1.0で、sinとcosを斜めに進めるのを足し合わせる感じになっている。

このパターンは、循環しているいい感じのパターンなら他でも良さそう。 という事で他のパターンも考えてみよう。
円のパターン
こういう感じの円はどうだろう?
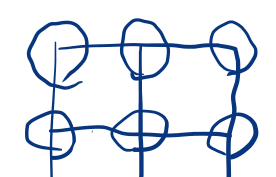
中心のあたりが黒くて円周のあたりで白になるようなもの。円周のサイズは格子サイズの半分か1/4がいいかな。 適当に試して見てみよう。
fn circle_pat |sh: f32v2, pscale: f32| {
let gsize = 6.0
let sxy = sh*pscale
let cxy = round(sxy/gsize)*gsize
let rxy = sxy - cxy
smoothstep(gsize/6.0, gsize/2.0, length(rxy))
}

まぁ書いた通りではある。smothstepは適当にそれっぽい放射状になるようにしている。
円の外周パターン
円の外周を4つ張り合わせたような、ひし形みたいなパターンも良くあるよな。 円の白と黒を逆にしてsmoothstepを逆にすればいいと思うんだが。
えーと、以下の式だよな。
smoothstep(gsize/6.0, gsize/2.0, length(rxy))
lengthをgsize/2.0-lengthにして、smoothstepを適当に調整すればいいか。
いろいろ出力を見つつ調整して以下になる。
smoothstep(0.0, gsize/8.0, gsize/2.0-0.8*length(rxy))
関数全体ではこんな感じ。
fn inv_circle_pat |sh: f32v2, pscale: f32| {
let gsize = 6.0
let sxy = sh*pscale
let cxy = round(sxy/gsize)*gsize
let rxy = sxy - cxy
smoothstep(0.0, gsize/8.0, gsize/2.0-0.8*length(rxy))
}

イメージしていたものにはなった。