03 Vectorized Operations and rsum

Previous: 02 Input and Basic Calculations

This time, we will look at vectorized operations, which perform multiple processes at once. We will also look at the command rsum, which is equivalent to loops in other languages.

Blur

It is known that an efficient method for blurring is adding vertically, then adding that result horizontally. This time, we will learn about vectorized arithmetic and rsum, using this blur processing as the subject.

Here we will look at the blur processing of 3x3 total, 1px up and down and 1px left and right.

Horizontal 3px blur

Ultimately, what we want to do is find the average for each of the top and bottom and left and right. But this is a bit difficult to explain, as you have to write the same process nine times.

So, first we'll look at the blur process that averages the left and right adjacent pixels, and then look at how to write this in a concise way.

Border treatment with ClampToEdge

First, when adding left and right pixels, you need to think about what to do with the pixel outside of border.

If you blur on average, it is best to assume that the color at the very end is repeated on the outside as well. This can be achieved using the sampler, which I mentioned a little bit last time.

Here, the code below treat border as such:

let inputEx = sampler<input_u8>(address=.ClampToEdge)

This sampler treats pixels beyond border as edge color (.ClampToEdge).

Simple Copy Paste Duplicate and Overflow

If you do the same processing as last time, it will look like following, but this will not work as it will exceed 8 bits.

@title "Horizontal blur trial(overflow)"

let inputEx = sampler<input_u8>(address=.ClampToEdge)

def result_u8 |x, y| {
  let [bm1, gm1, rm1, am1] = inputEx(x-1, y)
  let [b0, g0, r0, a0] = inputEx(x, y)
  let [b1, g1, r1, a1] = inputEx(x+1, y)

  # bm1+b0+b1 result might becomes more than 8bit.
  u8[(bm1+b0+b1)/3, (gm1+g0+g1)/3, (rm1+r0+r1)/3, (am1+a0+a1)/3]
}

In conclusion, the correct answer is to enclose the i32 as follows:

  let [bm1, gm1, rm1, am1] = i32(inputEx(x-1, y))
  let [b0, g0, r0, a0] = i32(inputEx(x, y))
  let [b1, g1, r1, a1] = i32(inputEx(x+1, y))

  # bm1 becomes i32, and so on.
  u8[(bm1+b0+b1)/3, (gm1+g0+g1)/3, (rm1+r0+r1)/3, (am1+a0+a1)/3]

This is not clean way, but working correctly. Below we will explain the briefly about overflow, but as an introduction, it will be a bit more detailed, so you can skip it at first.

Additional notice: if you're a person who is knowledgeable about image processing, you might wonder "Is this okay for Alpha?" Or "How aboutgamma correction?". But this time I will simply average without thinking about it.

Explanation of Overflow and Types (for Advanced Users)

When you create variables like following:

  let [bm1, gm1, rm1, am1] = inputEx(x-1, y)

The type of these variables are u8, which means unsigned 8bit integer.

If you add up three variables like following:

bm1+b0+b1

The result might be overflow.

So before doing the calculation, you need to cast it to i32. Cast can be done with i32(). Specifically, I will write it as follows:

  let [bm1, gm1, rm1, am1] = i32(inputEx(x-1, y))
  let [b0, g0, r0, a0] = i32(inputEx(x, y))
  let [b1, g1, r1, a1] = i32(inputEx(x+1, y))

  # bm1 becomes i32, and so on.
  u8[(bm1+b0+b1)/3, (gm1+g0+g1)/3, (rm1+r0+r1)/3, (am1+a0+a1)/3]

If you cast the right side like this, the variable itself becomes i32. You can also cast the tuples all at once.

Note that, as a GPU program, it is compiled as an unsigned 8-bit variable, but on many hardware this code actually works without overflowing. The handling of variables other than 32-bit in GPU programs is quite vague, and how it works when writing incorrect code is left to the hardware and the environment to some extent. As a MFG program, we recommend writing it to correctly calculate as the i32.

In MFG, the types are i, u, and f, and numbers representing the number of bits. i is a signed integer, u is an unsigned integer, and f is a floating point number.

Basically, the GPU has 32 bits registers, so the basic is to use i32 for integers and f32 for floating point numbers. However, formats that have BGRA in 8bit and 16bit each are often used, so using these values, the variables becomes u8 or u16.

In MFG, the integer constant is always i32. The type does not change automatically like in C language.

Tuples and swizzle operators

Now, it's really troublesome to put b, g, r, a separately in variables. Therefore, it is better code which put the tuple itself in a variable.

For example, following code:

  let [bm1, gm1, rm1, am1] = i32(inputEx(x-1, y))

can be change to use one variable only.

  let colm1 = i32(inputEx(x-1, y))

This is a tuple of four elements.

To access each element, you can use destructuring as follows,

  let [bm1, gm1, rm1, am1] = colm1

Or you can use swizzle operator to access elements.

  let bm1 = colm1.x
  let gm1 = colm1.y
  let rm1 = colm1.z
  let am1 = colm1.w

The swizzle operator can also access multiple elements as tuple.

  let [bm1, am1] = colm1.xw

Using this you can write as follows:

def result_u8 |x, y| {
  let colm1 = i32(inputEx(x-1, y))
  let col0 = i32(inputEx(x, y))
  let col1 = i32(inputEx(x+1, y))

  u8[(colm1.x+col0.x+col1.x)/3, (colm1.y+col0.y+col1.y)/3, (colm1.z+col0.z+col1.z)/3, (colm1.w+col0.w+col1.w)/3]
}

Code becomes a little shorter.

Vectorized Operations

It is often the same calculations are performed for each of the elements x, y, z, and w, and this can be performed together as vectorized operations.

For example, if you add two elements to create a new tuple, as follows:

  let res = [colm1.x+col0.x, colm1.y+col0.y, colm1.z+col0.z, colm1.w+col0.w]

You can do it at once like following:

  let res = colm1+col0

This is called "Vectorized Operations".

In addition to +, this can be done using functions that support addition, subtraction, multiplication, and division, some vectorized supported function, or ifel. Using this, the program above can be written in a compilation as follows:

@title "Horizontal Blur"

let inputEx = sampler<input_u8>(address=.ClampToEdge)

def result_u8 |x, y| {
  let colm1 = i32(inputEx(x-1, y))
  let col0 = i32(inputEx(x, y))
  let col1 = i32(inputEx(x+1, y))

  u8((colm1+col0+col1)/3)
}

You need to cast it to u8.

You were able to calculate the average all at once.

Use rsum to make the process at once

In other languages, loops can be used to perform this kind of task. A similar feature in MFG is called rsum.

Using this you can write as follows:

def result_u8 |x, y| {
  let col = rsum(0..<3) |i| {
    i32(inputEx(x-2+i, y))
  }

  u8(col/3)
}

rsum stands for reduce sum, which executes the specified range block and returns the sum. A new term called block has emerged, so let's take a closer look.

rsum and block

rsum takes a range in the argument. Supported dimensions are: one dimension and two dimensions.

# 1D
rsum (0..<3) |i| { i+2 }

# 2D
rsum(0..<3, 0..<5) |i, j| { i+j+5 }

If you write 0..<3 etc., the range is considered to be 0, 1, and 2 in order. Please note that 3 is not included.

Runs a block to the specified range. The blocks are in the following form:

|i| {
  # Write expression here
}

i is the block's formal argument, and in the case of rsum, numbers are comming in order. i's name can be anything.

In the case of 2D, these are two.

|i, j| {
  # Write expression here
}

rsum returns the result of adding up the results of evaluating the expression.

rsum is similar to a normal language loop, but there are some restrictions.

• You cannot widen the loop halfway through (execute as many times as you have decided at the beginning)
• There is no way to end in the middle of a loop (all iterations are always executed)

This is designed in line with the actual GPU mechanism.

Incidentally, the range does not need to be from 0. You can also start with -1 as follows:

  let col = rsum(-1..<2) |i| {
    i32(inputEx(x+i, y))
  }

Note that the ending specification is 2 even though the actual value range is from -1 to 1.

Simplest blur treatment

Using the above, we will also perform calculations to calculate the sum in the vertical direction.

@title "Simple Blur"

let inputEx = sampler<input_u8>(address=.ClampToEdge)

def result_u8 |x, y| {
  let sum = rsum(0..<3, 0..<3) |i, j| {
    i32(inputEx(x-2+i, y-2+i))
  }
  u8(sum/9)
}

Since it has only 1px front and back, it is difficult to see the effect unless you enlarge it, but it is as follows.

Before blur	After blur

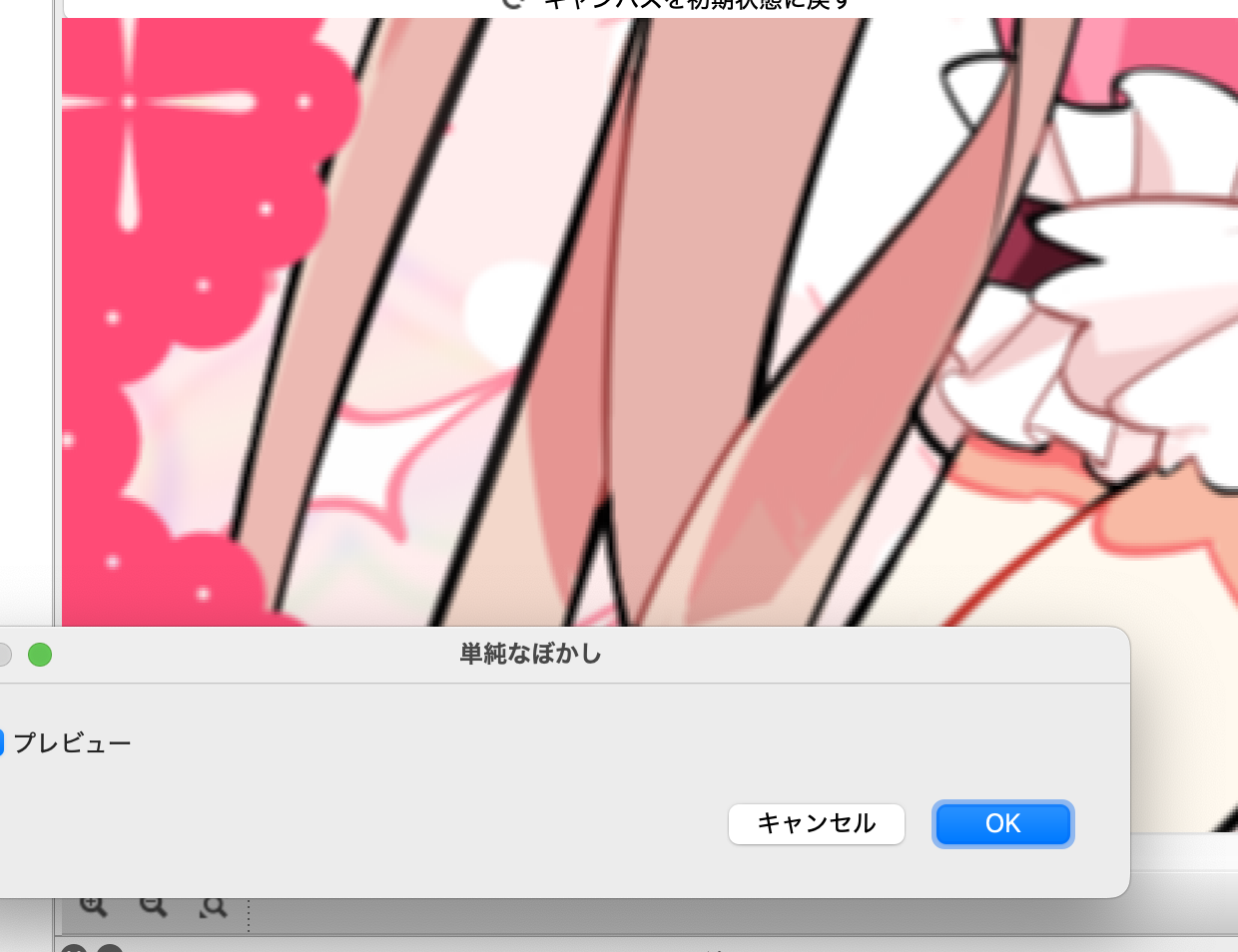Summary of this chapter

• You can accept colors as tuples into one variable
• There is a vectorized operations that allows you to add or divide tuples together
• You can retrieve elements from a tuple using the swizzle operator
• You can write the process of repeating and adding up specified ranges in rsum

Next

04 Intermediate tensors for complex algorithms