MFGでプログラムをするためには、GPUでのプログラム、というものに慣れる必要があります。

そこでこここでは、GPUのプログラムの特徴が一番良く出る基本図形の描画について見ていきましょう。 基本図形の描画は直接フィルタとしては使わないものですが、 高度なフィルタでは内部で部分的に必要になる事も多く、基本を理解しておく事には意味もあります。

なお、CPUで同種の話をした書籍に amazon: 2Dグラフィックスのしくみ ――図解でよくわかる画像処理技術のセオリー という書籍がFireAlpaca開発チームから出ています。 こちらは数学の解説などもより詳細かつ予備知識を前提とせずに詳しく行われているので、 CPUで実装する場合との違いを学びたければ比べてみると面白いでしょう。

今回の記事はMFG Studioで開発、動作確認しています。

書いてみたら思ったより長くなったため、前後編に分けます(^^;

  • 前編は縦の垂線と円
  • 後編は斜めの線と三角形

縦の直線を描こう

図形で一番カンタンなのは縦に線を引く、というものです。 まずは左から300pxの位置に幅3pxの線を引く、というのをやってみましょう。

スクリプトは以下のようになります。

let fgcol = u8[0, 0, 0xff, 0xff]
let bgcol = u8[0, 0, 0, 0]

def result_u8 |x, y| {
  ifel( abs(x - 300) <= 1, fgcol, bgcol )
}

実行すると以下のようになります。

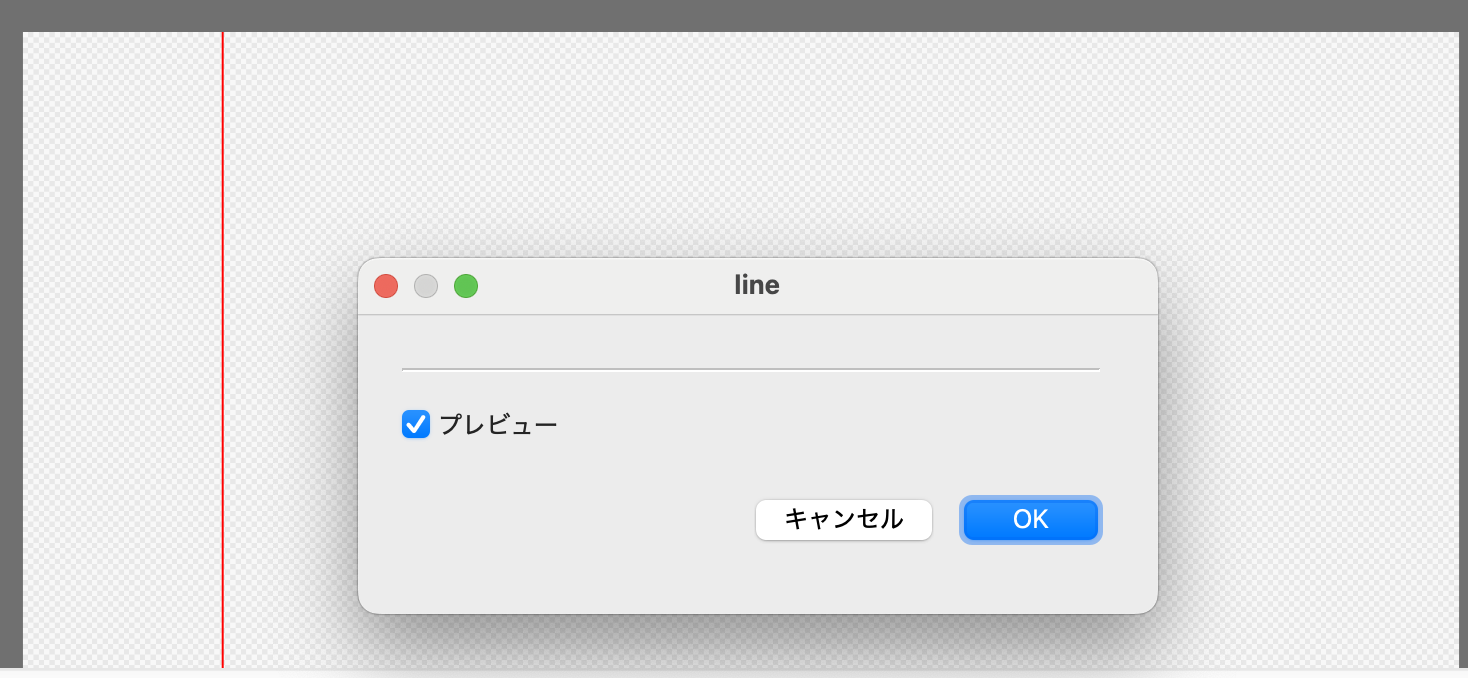
images/MFG_BasicShape/2025_0724_132356.png

コードとしては、xが299, 300, 301の時はfgcolを、それ以外はbgcolを返す、という挙動となります。

fgcolは赤、bgcolは透明となります。

ノーマライズされた座標と色を使う

ピクセルでプログラムをすると、画像サイズが変わった時にコードも変わるため、その対応でコードが複雑になりがちです。 そこでGPUでのグラフィックスプログラムではf32の浮動小数点でコードを書くのが一般的です。

その場合は0.0〜1.0にノーマライズされた座標を使います。

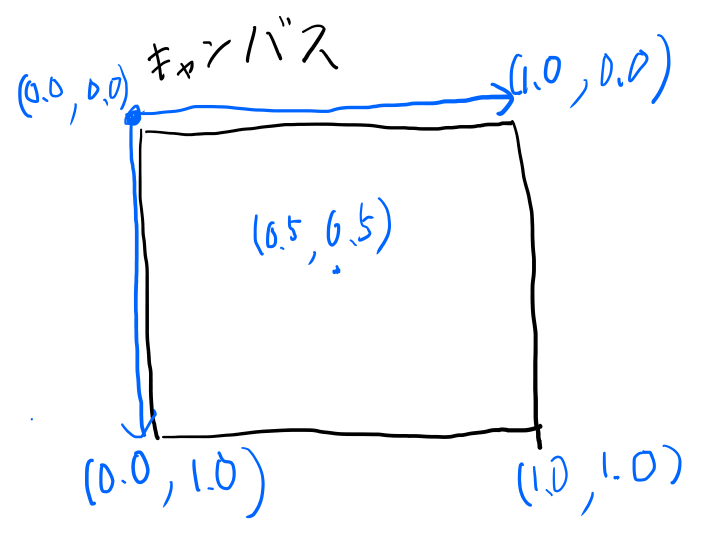
images/MFG_BasicShape/2025_0724_140923.png

こうするとキャンバスのサイズによらずプログラムが可能です。 座標を浮動小数点にするにはto_ncoordを使います。

let fgcol = u8[0, 0, 0xff, 0xff]
let bgcol = u8[0, 0, 0, 0]

def result_u8 |x, y| {
  let [fx, _] = to_ncoord([x, y])
  ifel( abs(fx - 0.3) <= 0.001, fgcol, bgcol )
}

images/MFG_BasicShape/2025_0724_141358.png

300と指定していた所を0.3として、幅を0.001としています。 画像全体の幅を1.0とした時の0.3というのはわかりやすいですが、幅が0.001というのがどのくらいか、というのは少し直感的では無いですね。

座標と同様に、色もf32の0.0〜1.0の範囲のノーマライズされた値を使う事も頻繁にあります。 これも使ってみましょう。

let fgcol = [0.0, 0.0, 1.0, 1.0]
let bgcol = [0.0, 0.0, 0.0, 0.0]

def result_u8 |x, y| {
  let [fx, _] = to_ncoord([x, y])
  ifel( abs(fx - 0.3) <= 0.001, fgcol, bgcol ) |>
  to_u8color(...)
}

to_u8colorではパイプライン演算子を使っています＞MFGのパイプ演算子を実装した - なーんだ、ただの水たまりじゃないか

浮動小数点の計算が早い、というのはCPUとGPUが大きく違う所です。 レジスタも大量に用意されているし、ハードウェアとして浮動小数点演算が大量に並列に行えるようになっています。 i32と比較してどのくらい遅くないのかはハードウェアによる上に近年の複雑なGPUではかなり評価が難しい要素になりますが、 入門レベルではf32はi32と同じ感覚で使っていくのがGPUプログラムとしては適切です。

位置と幅、色をwidgetで指定出来るようにする

fgcolと0.3、0.001などはハードコードされていて、基本図形を描くという点ではこれで良いのですが、 少し脱線してMFGの勉強としてこれらをwidgetで指定出来るようにしてみましょう。

（なおCOLOR_PICKERはv1.0.02で実装された機能なので最新版にアップデートしないと動かないかもしれません）

@param_f32v4 fgcol(COLOR_PICKER, label="線の色")
@param_f32 xpos(SLIDER, label="位置", init=0.3, min=0.0, max=1.0)
@param_f32 width(SLIDER, label="幅", init=1.0, min=0.1, max=500.0)

let bgcol = [0.0, 0.0, 0.0, 0.0]

def result_u8 |x, y| {
  let [fx, _] = to_ncoord([x, y])
  ifel( abs(fx - xpos) <= width*0.001, fgcol, bgcol ) |>
  to_u8color(...)
}

幅のような小さな数字をスライダーでいい感じに指定するのはちょっと難しいので、1/1000倍して使うようにしています。

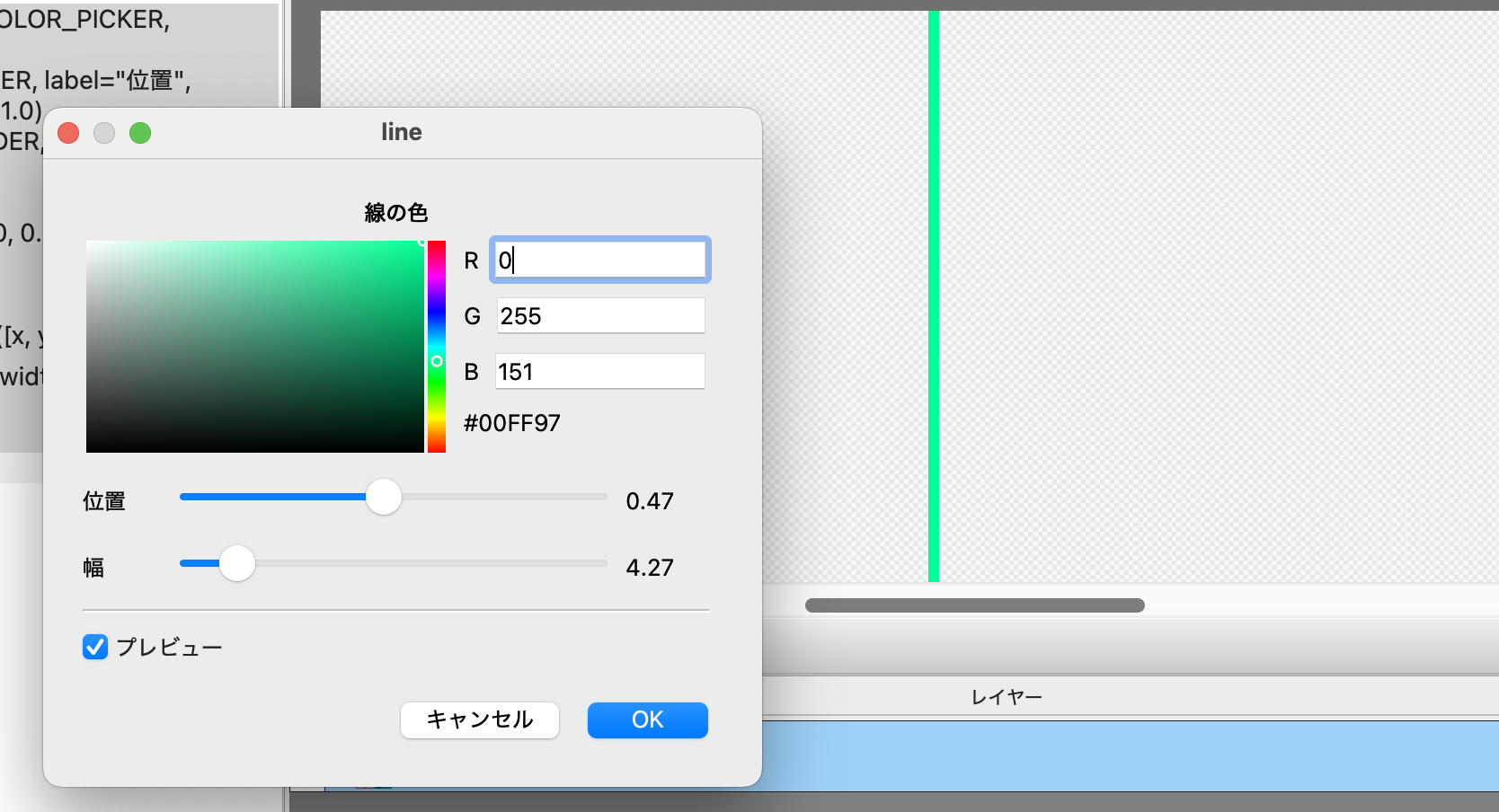
images/MFG_BasicShape/2025_0724_143003.png

対話的に色を変えたり幅を変えたりが簡単に出来るのはMFGのいい所ですね。

円を描く

垂直と水平の線は少し単純過ぎるので、もう少しだけプログラムとして複雑になる、円の描画について見てみましょう。 なお、以下では本題の基本図形の描画に集中するため、パラメータは全てハードコードして書いていきます。

縦横に歪んだ楕円を描く

何も考えずにノーマライズされた座標で円を描くと、キャンバスサイズの縦横比に応じて楕円になってしまいます。 まずは一番単純なコードで楕円を描いてみましょう。 0.5から半径0.1の楕円を描いてみます。

let fgcol = [0.0, 0.0, 1.0, 1.0]
let bgcol = [0.0, 0.0, 0.0, 0.0]

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])
  let dxy = fxy - 0.5
  ifel( length(dxy) < 0.1, fgcol, bgcol ) |>
  to_u8color(...)
}

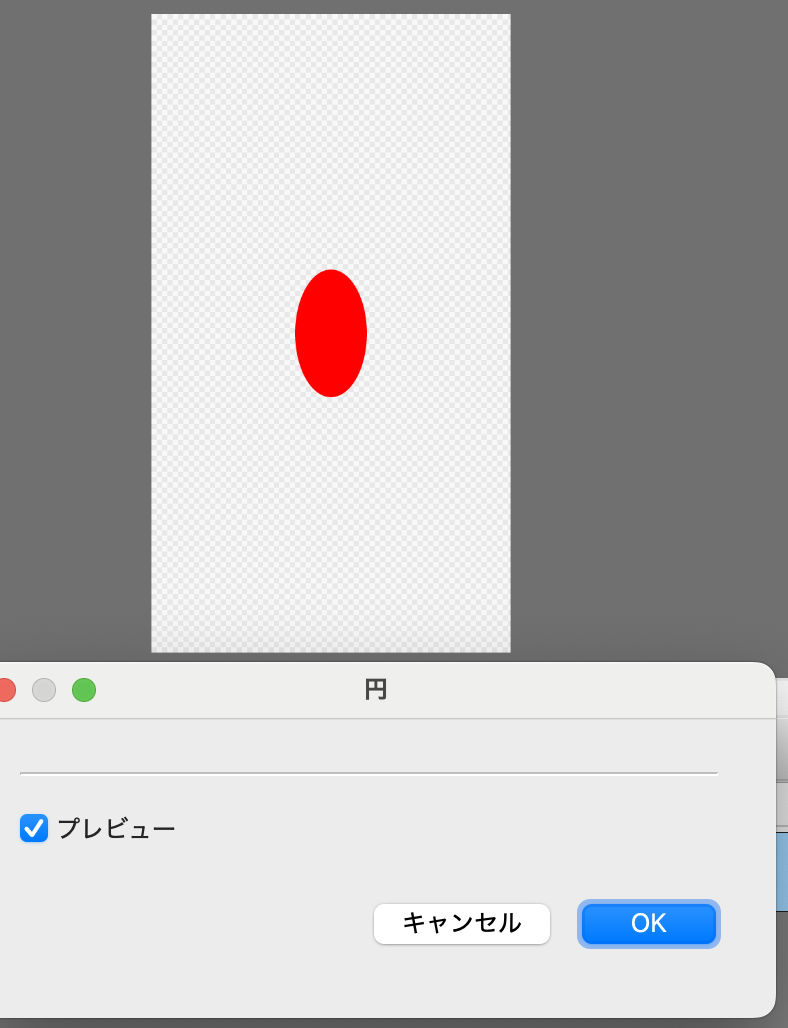
images/MFG_BasicShape/2025_0724_144424.png

さて、さらっと描きましたが、ベクトル演算を使っているのでちょっとトリッキーです。 あまりベクトル演算に馴染みが無い人のために、少し寄り道してベクトル演算の説明をしましょう。

ベクトル演算を見ていく

以下の部分がベクトル演算を使っている所です。何をしているかわかりますか？

  let fxy = to_ncoord([x, y])
  let dxy = fxy - 0.5

fxyというのは、f32の2要素のタプルです。 例えば [0.3, 0.7] とかそういう値が入っています。

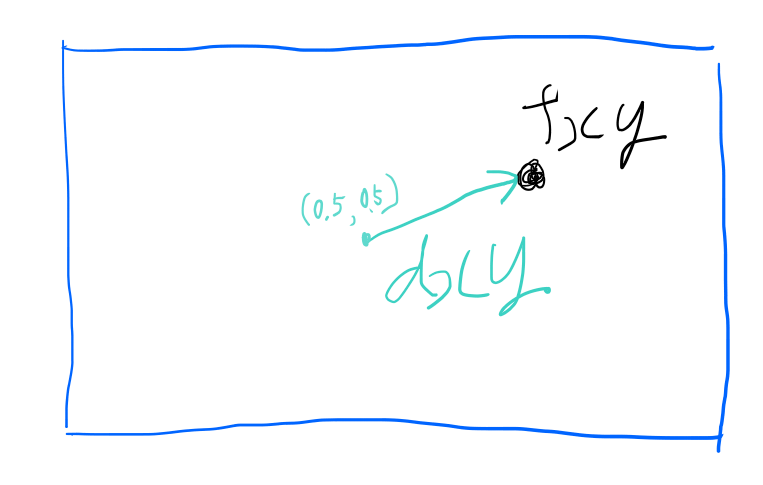
次の行の右辺では、 fxy - 0.5 という計算をしていますが、 これは先ほどの具体的な値の例を入れると、 [0.3, 0.7] - 0.5 となります。

ベクトルとスカラーの加減乗除は、基本的にはスカラーの値をそれぞれの要素に適用したのと同じ意味になります。 つまり、以下の式は全て同じ意味です。

  • [0.3, 0.7] - 0.5
  • [0.3, 0.7] - [0.5, 0.5]
  • [0.3-0.5, 0.7-0.5]

つまり、dxyは(0.5, 0.5)からのベクトルを表します。

images/MFG_BasicShape/2025_0724_223404.png

さらにifelの所ではlengthを使っています。

  ifel( length(dxy) < 0.1, ... )

この相対ベクトルを求めてlengthで距離を出す、というのはグラフィックスプログラムでは良くあるので慣れておくと良いでしょう。 ちょっと高校生の数学っぽいですね。

CPUでの円の描画との違いを考える

CPUで円を描く場合は、円の一番上の点から始めて、yを1ずつ下げていき、各yで最小のxと最大のxを求めてその間を塗りつぶすのが良くやられる方法です。

図にすると以下のようになります。

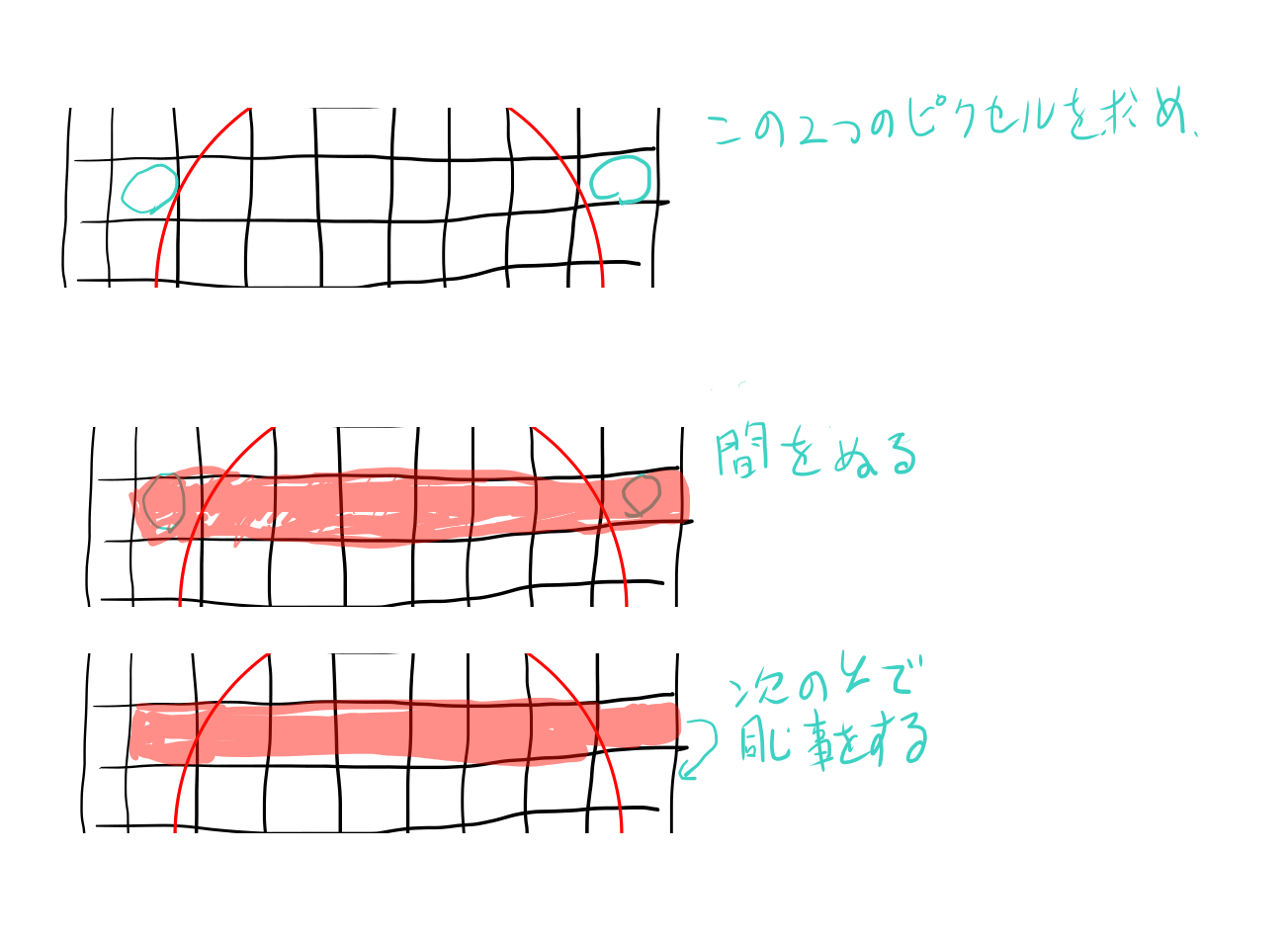
images/MFG_BasicShape/2025_0725_231956.png

このようにすると、円の大きさ程度のピクセルしか操作する必要が無いし、円の最後まで行ったらそこで計算を終える事が出来るため、 キャンバスの大きさでは無く円の大きさ程度の複雑さで済みます。 各yで最小値と最大値を計算するのは一回だけです。 それぞれのyでも幅の分しかメモリにアクセスする必要はありません。 とても早く終わりそうです。

一方、GPUの描画では、全ピクセルについて、皆が円の方程式の計算をします。円が描かれないピクセルでも全部計算します。 円が描かれる所だけを計算する、というのはGPU的ではありません。いつも全ピクセルが同じ計算をします。 円が描かれ終わった所で計算を終える事も出来ません（そもそも並列で動くので前後関係がわからない）。

CPUが描かれる図形の所だけしか計算の必要が無い事に比べるとすごく無駄が多く感じますね。 でもそのおかげで並列に計算をする事が出来るようになります。

GPUでのグラフィックスプログラムというのは、たとえると、ピクセルの数だけ人を用意して、 それぞれの人にあたなは何色を描きますか？と聞いて答えた色を描いていくようなものです。 聞き手もたくさんいて、それぞれ分担して同時に聞いていきます。 他の人がなんて答えたのかは知る方法が無く、各自がそれぞれ円の方程式を解いて、自分の座標の色を答える訳です。

この全ピクセルに同じ計算が動く、というスタイルでアルゴリズムを考えるのが、GPUでグラフィックスプログラムをするという事の根幹です。

歪んでない円を描く

さて、先ほどのコードではキャンバスのアスペクト比で歪んでしまっていました。

これは縦か横のどちらかの比率で揃える事で修正出来るはずです。横に統一するために、 y方向の差分に「高さ/幅」を掛けてみましょう。

比率は以下のようになるので

  let fwh = input_u8.extent() |> f32(...)
  let ratio = fwh.y/fwh.x

全体としては以下のようになります。

let fgcol = [0.0, 0.0, 1.0, 1.0]
let bgcol = [0.0, 0.0, 0.0, 0.0]

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])
  let dxy = fxy - 0.5
  let fwh = input_u8.extent() |> f32(...)
  let ratio = fwh.y/fwh.x
  let dxy2 = dxy * [1.0, ratio]
  ifel( length(dxy2) < 0.1, fgcol, bgcol ) |>
  to_u8color(...)
}

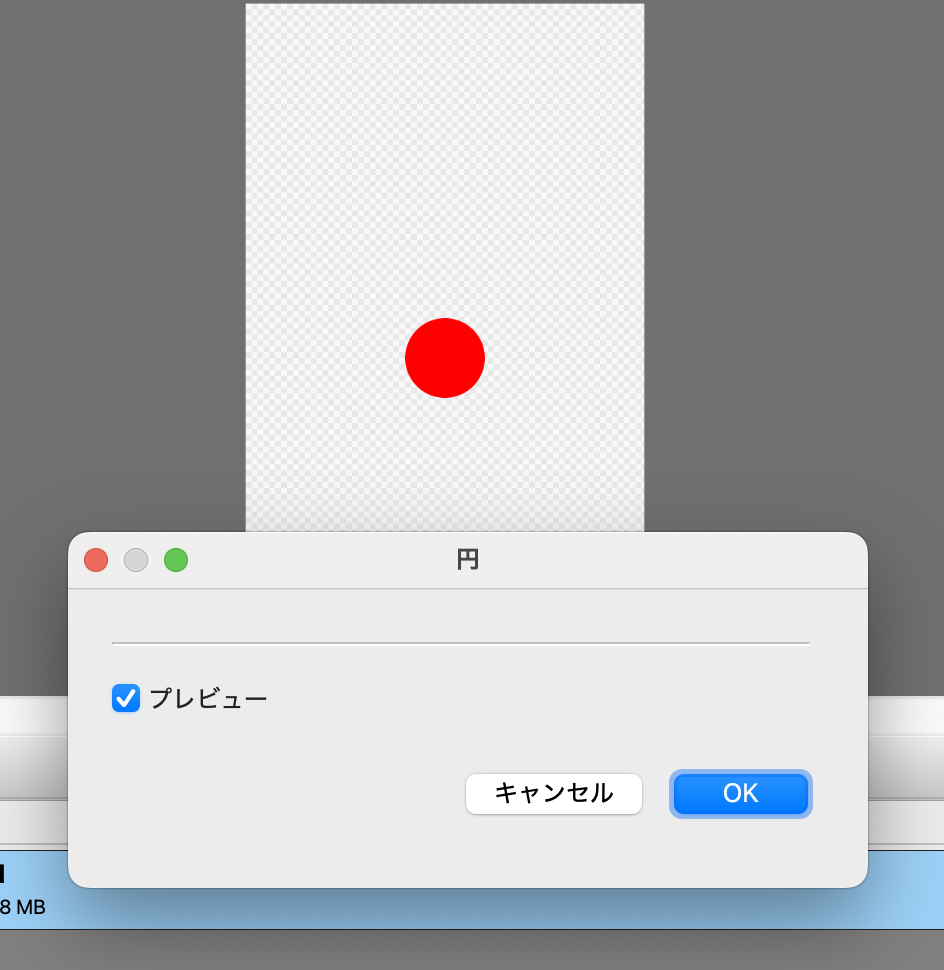
images/MFG_BasicShape/2025_0724_225218.png

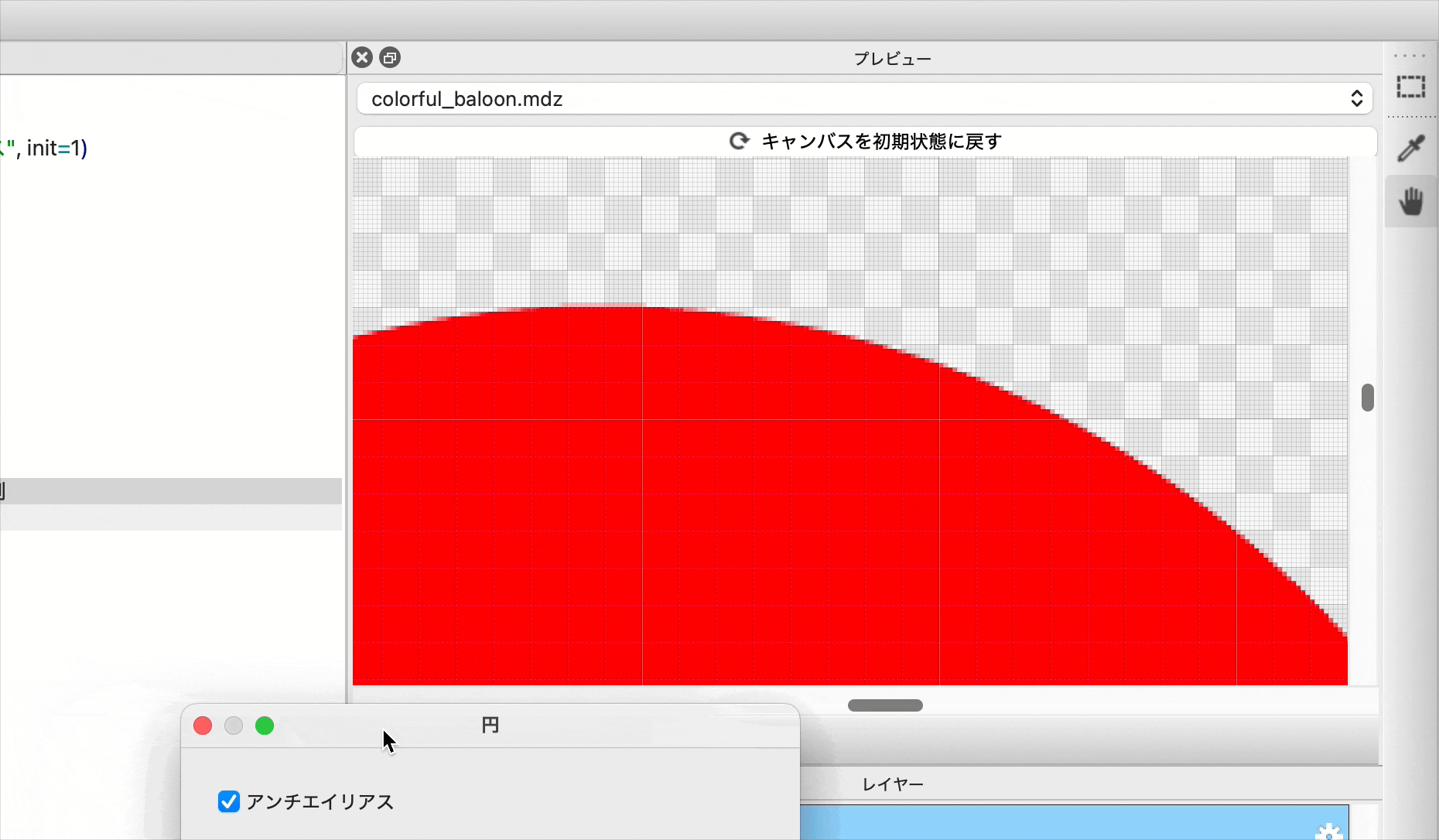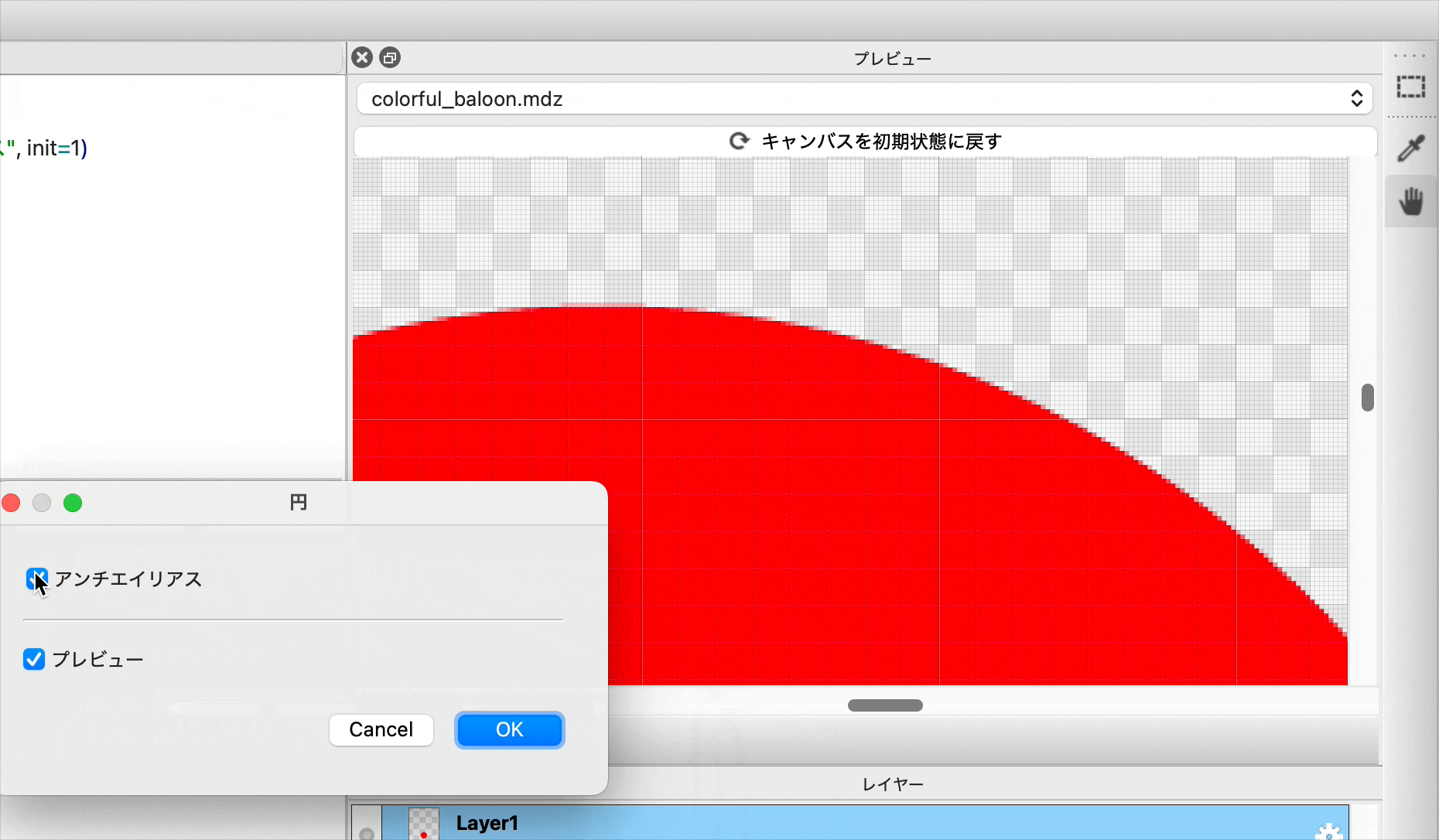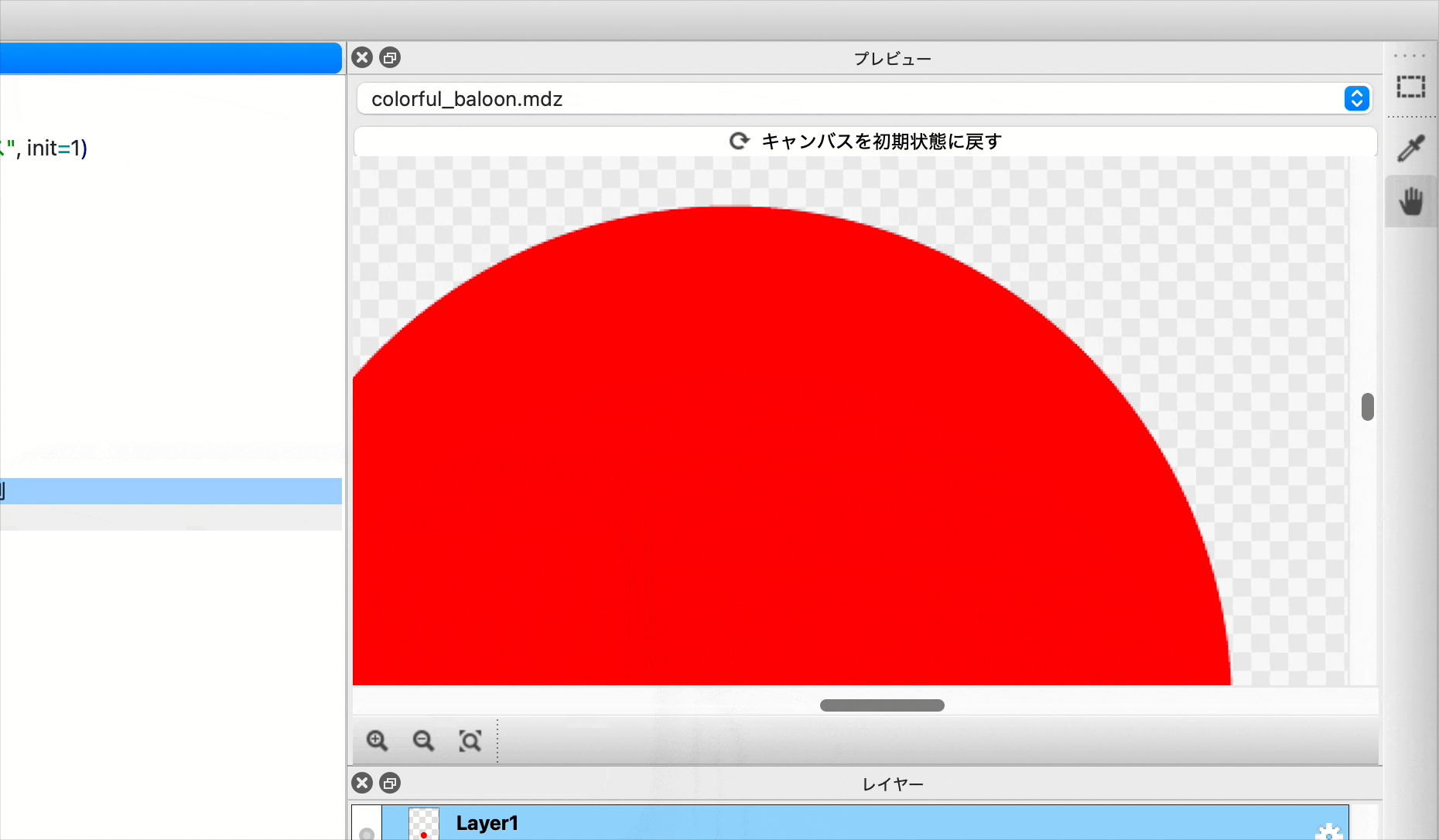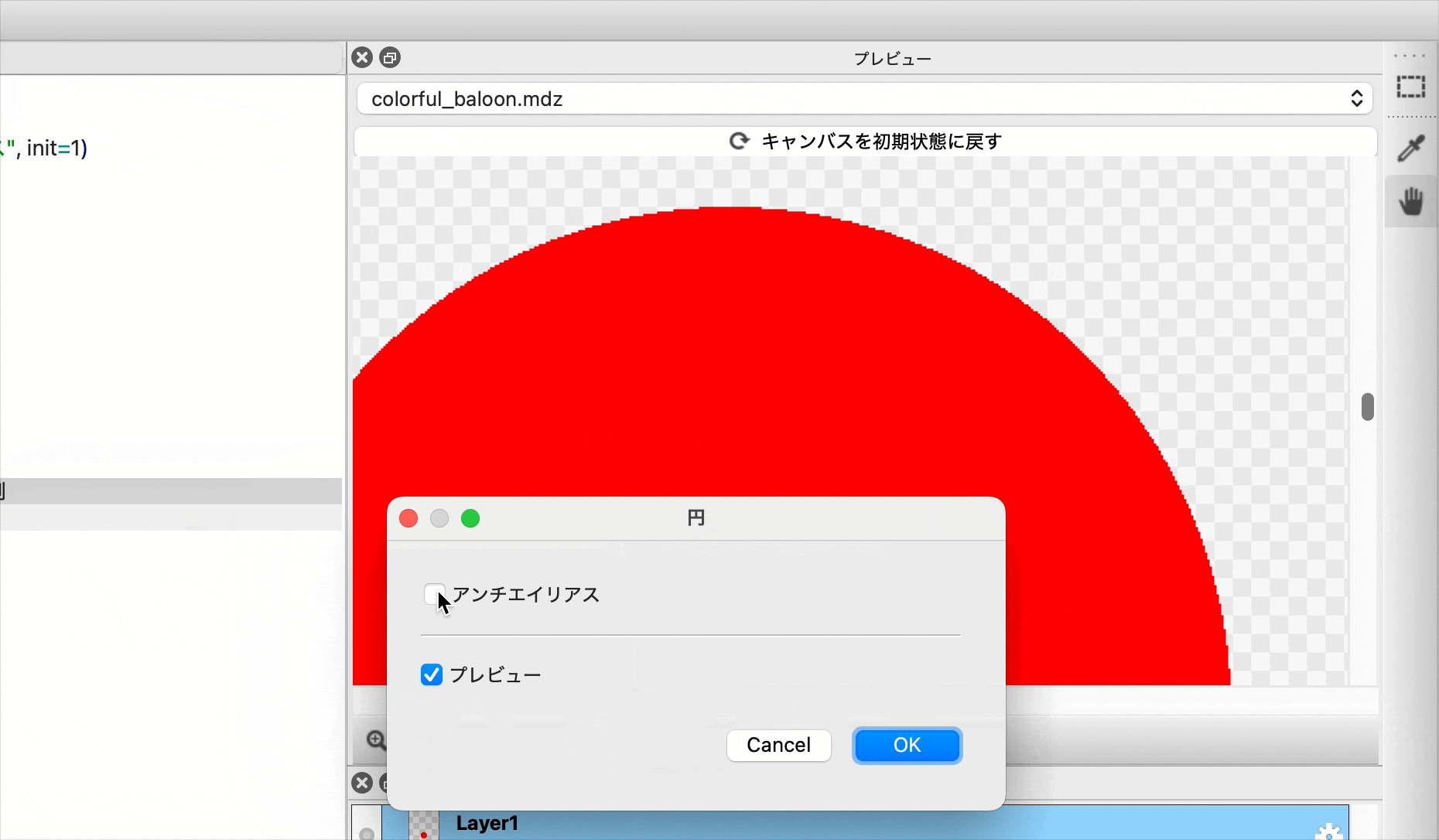
無事円になりました。

エイリアスを見てみる

円を拡大してみると、端がギザギザしています。

images/MFG_BasicShape/2025_0724_225557.png

これは、ピクセルというのは実際は点では無くて小さな四角形なのに、左上の点が入っているか入っていないかで全てを計算しているせいです。

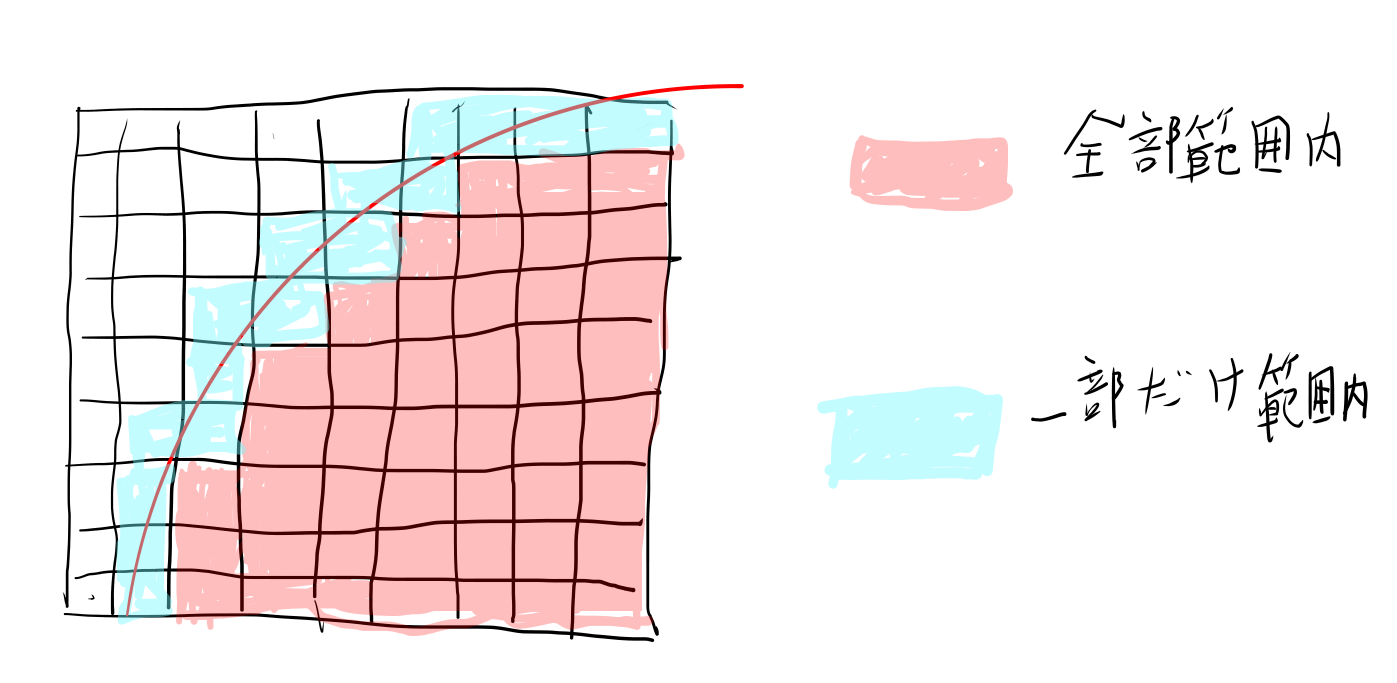
images/MFG_BasicShape/2025_0725_114546.png

この図の部分的に範囲に掛かっているピクセルは、本来はその入っている量に応じてアルファ値で処理すべき範囲になりますが、 現状のアルゴリズムでは0か1かになってしまいます。

サブピクセルでキレイな円を描く

部分的に掛かっているピクセルの被覆割合を計算する方法はいろいろ考えられますが、 元のアルゴリズムから一番変更が少なく単純なのはサブピクセルに分割する方法でしょう。

ピクセルを、例えば4x4の16分割をしてこれまでと同じ計算をし、引っかかる個数の割合を被覆割合とする、というものです。

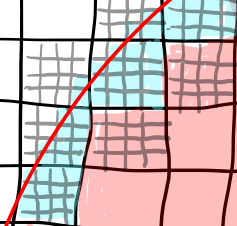
images/MFG_BasicShape/2025_0725_131151.png

サブピクセルに分けても、端に掛かっているサブピクセルが0か1かになってしまう事には代わりありませんが、1ピクセルの1/16程度のオーダーでは正確な被覆率となります。 やってみましょう。

このように一つのピクセルに対してループを実行する場合、MFGではrsumを使います。

let divNum = 4

def result_u8 |x, y| {
  let fxy = to_ncoord([x, y])
  let fwh = input_u8.extent() |> f32(...)
  let ratio = fwh.y/fwh.x
  let eps = 1.0/(fwh*divNum) # 1ピクセルあたりの差分を4分割
  let coverSum = rsum(0..<divNum, 0..<divNum) |rx, ry| {
    let fxy2 = fxy + f32[rx, ry]*eps
    # あとは先程と同じ
    let dxy = fxy2 - 0.5
    let dxy2 = dxy*[1.0, ratio]
    # 結果を色では無く0, 1で返して割合にする
    ifel( length(dxy2) < 0.1, 1.0, 0.0)
  }
  let coverRatio = coverSum/(divNum^2)
  [*fgcol.xyz, coverRatio*fgcol.w] |> to_u8color(...)
}

images/MFG_BasicShape/2025_0728_201048.png

キレイな円になりました。 拡大しているとすごくキレイという感じでも無いですが、ふつうのサイズだとキレイな円です。

このコードをぱっと見て理解するのはなかなか難しいですね。 ただ、良く見ると前のコードでfxyを使っていた所をfxy2にするだけ、という事を理解できれば、 fxy2をどうやって作っているかに着目すれば良くなります。

fxy2は以下のように作っています。

  let eps = 1.0/(fwh*divNum) # 1ピクセルあたりの差分を4分割
  # 中略
    let fxy2 = fxy + f32[rx, ry]*eps

epsというのは、ノーマライズされた座標で、1ピクセルの幅を4分割したものが幾つになるか、という値を表します。 そして rx, ry はrsumのループ変数なので、0から3までの値をとるので、これでサブピクセルのノーマライズされた座標を計算している事になります。

このサブピクセルで範囲に入っていれば1.0、入っていなければ0.0として足し合わせて、合計を4x4で割れば被覆率となります。 この被覆率でfgcolのアルファを変更しています。

[*fgcol.xyz, coverRatio*fgcol.w]

アスタリスクはspread演算子で、展開したものがタプルの要素となります。最後のw要素だけcoverRatioを掛けているのですね。

この手の処理をする場合、この処理をするかしないかでどのくらい違いがあるかを見てみると面白いので、 少しコードが複雑になりあｍすが、チェックボックスをつけてオンオフ出来るようにしてみましょう。 以下のようなコードになります。

@param_i32 ANTI_ON(CHECKBOX, label="アンチエイリアス", init=1)
# 以下同じ

def result_u8 |x, y| {
  # 前と同じ
  # 最後だけ以下に変更
  let coverRatio = coverSum/(divNum^2)
  let cr = ifel(ANTI_ON, coverRatio, step(0.99, coverRatio))
  [*fgcol.xyz, cr*fgcol.w] |> to_u8color(...)
}

ステップ関数の所は全部が範囲内だと1とするとか、0.5以上だと1とするか、全部0でなければ1とするか、どれもあり得る選択だと思います。

適当な拡大率でアンチエイリアスのある無しでどのくらい違うのかを見ると面白いです。

images/MFG_BasicShape/2025_0728_201808.gif

後編に続く

MFGで基本図形を描いてみよう（後編） - なーんだ、ただの水たまりじゃないか