勉強会向けIBの論文読み

[physics/0004057] The information bottleneck method

以前ざっと読んだが、勉強会でこれをやりたい、との事なので、今度はもっと真面目に計算とかを追う。

定理1の証明

式10が突然出てくるので、まずはここから。

とりあえずFの定義を書き下す。

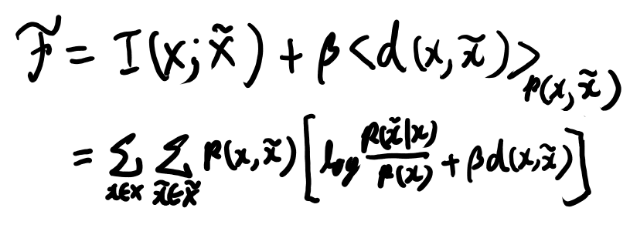
次にこれの、mapping（条件付き確率）による変分を考える。 ゆとりなので変分の公式がすぐに出てこないので、昔のブログを探す。

Cover and ThomasのMEの所か。 十二章〜最後までの最初のところ。

離散的なケースもまぁクロネッカーデルタと思っときゃいいんだろう、たぶん（ゆとり）。

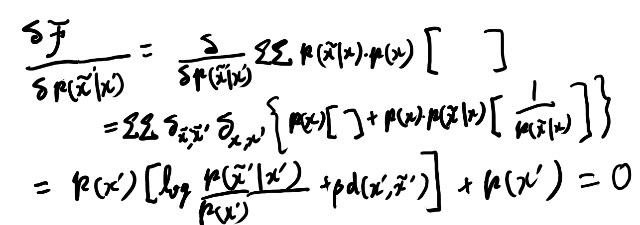
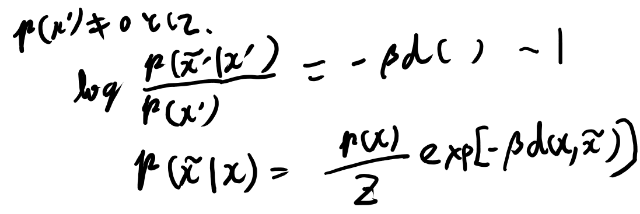
なんかあってそうに思ったが、そのあと式9を見るとベータが違いそうだな。

そうか、ノーマライズされなさそうだよな、これだと。 だから制約条件をLagrange multiplierで入れないとダメだよな。

制約としては、xの事前分布とxチルダの条件付き確率の規格化条件だよな。 で、変分で事前分布はどうせ消えるので、こうか？

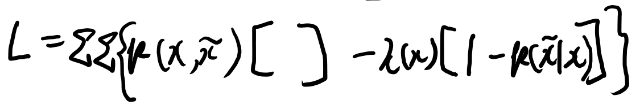
（追記: 上の式は間違いで、1じゃなくて1/(xチルダの要素数)が正解と思うが、結局変分で消えるので以後の結果は変わらない）

p(x)の制約が要らないかいまいち自信が持てないが。 変分してみよう。

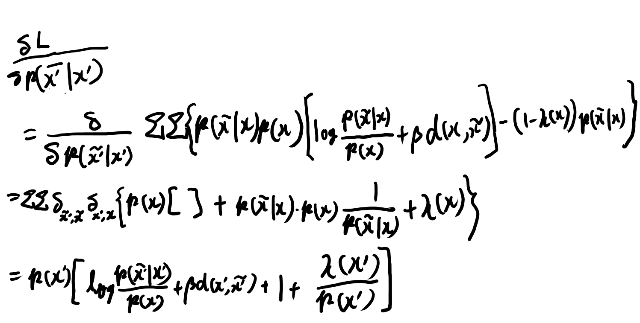
10式とは-1だけ（二行目第一項）ずれてるな。なぜだろう？

---

Slackで泣きついたところ、そもそも相互情報量の分母がチルダがついてたのを見落としてた事が判明。

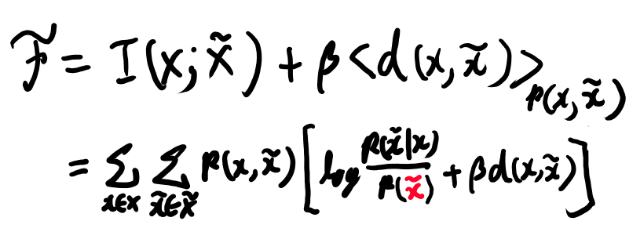
この場合、条件付き確率による変分の影響を考える為には、マージナライズの形に書き直せば良さそうか。

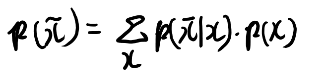
シグマが3つでデルタが2つなのでxについての和が残りそう。 なるほど、一致しそうだな。

関連する所だけ計算してみよう。

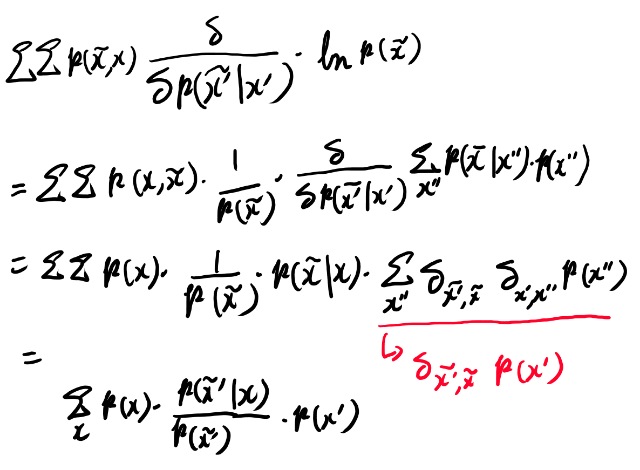
プライムの残り方がトリッキーだが最終的にはつじつまが合うようだ。見た目より難度高い計算だな。