MFGで高度なアンチエイリアス(MLAA)を実装してみよう(前編)
MFGはすぐに実際のアルゴリズムの実装に入れるため、GPUでの画像処理を学ぶのに非常に適しています。 ここでは実際に論文を実装してみる例として、高度なアンチエイリアスであるMLAA(MorphoLogical AntiAliasing)の実装を行ってみたいと思います。
なお、このブログの記事を書いていていくつかバグを見つけて修正したので、以下のコードを試す場合はMFGStudio v1.0.06(またはそれ以降)のバージョンで試してみてください。
アンチエイリアスとMLAA
エイリアスとは、感覚的な言い方をすれば画像をピクセルで扱う都合で生じる空間的な不連続さが、人間の目にとって目立って気になる現象です。
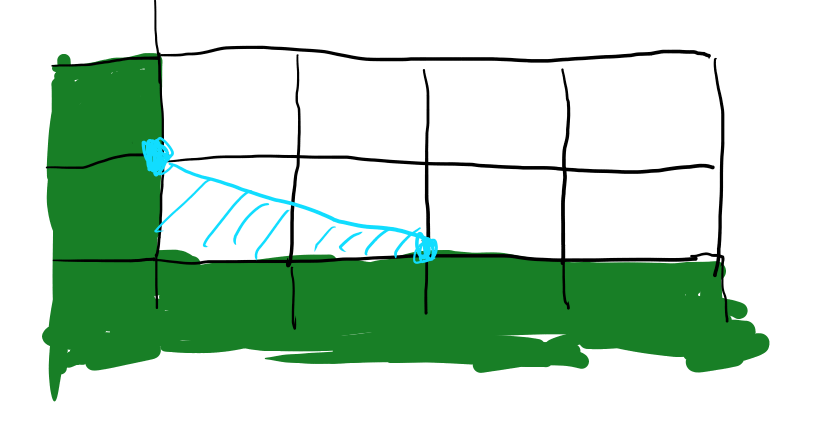
例えば斜めの線などを書く時に、アルファなどを使わずに段々で描くと、以下のようにエイリアスが出ます。

ガタガタしていていますね。
ピクセルの部分的に掛かる部分は、それに応じたアルファを指定することでこうしたガタガタをなめらかに出来ます。 このガタガタをなくす処理をアンチエイリアスといいます。 例えばこの記事で開発する予定のMLAAを適用すると以下になります。

ここでは、アンチエイリアスについての雑多な話と、現代的なGPUアンチエイリアスの基礎となっているMLAAについて実装をしつつ解説をしてみたいと思います。
いろいろなアンチエイリアス
アンチエイリアスは3D CGでは良く研究されている一大分野で、SIGGRAPHなどでも良く見かけるトピックです。
アンチエイリアスには、大きく
- 絵を生成する時に行うもの
- 既にある絵に対して行われるもの
があります。
絵を生成する時のアンチエイリアスは、これから描こうとしているものの、真の情報にアクセスすることが出来て、 それをもとにいつも正しいアンチエイリアスを行うことが出来ます。 CGの論文で良く出てくるものとしては、レイトレーシングや3Dのレンダリングパイプラインでのアンチエイリアスがあります。 反面、真の情報ごとに適切に実装する必要があり、また、真の情報が必要になるため、真の情報が失われている時にはうまく行きません。 また、レンダリングパイプラインの途中でシェーディングなどの処理を行いたい時に、 それらの結果発生するエイリアスなどに対処するには違うステージでの実装が必要になったり、 その計算量の予測が困難だったり、デメリットもあります。
例えば、先日やった 基本図形の描画 でやったような図形を描く時の、図形に応じたアンチエイリアス処理や、 ブラシで線を引く時などは、絵を生成する時に行うものです。
それに対して、最終的な結果の絵に対してpost processとして行うアンチエイリアスというものも多く研究されています。 3D CGではフィルターベースのアプローチとかpost processのアプローチとか言われたりします。 これは2次元の画像処理でも応用しやすく、解像度の荒い写真とか色数の少ない元画像を使いたいシチュエーションなど、 いろいろなシチュエーションで使うことが出来ます。 その反面、真のデータから行うものではないので、何かしらの経験則でたぶんエイリアスだろう、 と思う所を処理するため、その経験則に反した場所ではうまく行きません。
今回実装するMLAAは、後者のフィルターベースのアプローチのアンチエイリアスが流行り始めたきっかけとなった画期となる研究です。
MLAAの論文について
今回実装してみるアルゴリズムは、Intelの人が書いた、Morphological antialiasing、通称MLAAというアルゴリズムをベースに、 GPUでも動くように簡略化したものです。
Morphological antialiasing - Proceedings of the Conference on High Performance Graphics 2009
Intelのサイトで公開されているのですが、ちょこちょこURLが変わるようなのでGoogle Scholarなどでその都度検索した方がいいでしょう。 2009年の論文ですね。Google Scholarで2025年8月現在で131引用。なかなか引用されている論文。
以下のサイトに紹介ブログ記事があります。
Morphological Antialiasing - Real-Time Rendering
citeを見ると最近はニューラルネット系のものから引用されてそうですが、2010年代の前半に割と流行っていたトピックという印象です。
この論文ではCPUベースの実装となっていて、そのままではGPUでは実装出来ませんが、細部を少し変更すればGPUでも実装出来ます。 そのままの実装は見つかりませんでしたが、以下のAMDの実装がこの論文の実装を一部変更した上でDirectX 11で実装したものになっています。
GPUOpen-LibrariesAndSDKs/MLAA11: AMD morphological anti-aliasing (MLAA) sample based on DirectX 11
このコードを見ると既存のGPUプログラムの敷居の高さがわかりますね…
基本的なアイデア
フィルターベースのアンチエイリアスというのは、基本的にはエイリアスっぽい所を見つけて間を薄める、という処理になります。
エイリアスっぽいというのは、一番素朴には大きく色が変わる所、という事になりますが、 これだとすべての境界がただぼやけてしまうだけなので、エイリアスは減ってもシャープさがなくなってしまうという欠点があります。 くっきりとした垂直な直線の境界は、本来はエイリアスでは無いはずなのに、そういったところが全部ぼやっとしてしまうのはいまいちです。
そこで、エイリアスっぽい所だけをどうにか認識してそこだけ薄める感じの事がしたい。 MLAAとそれの後に続く発展的なアルゴリズムは、基本的にはこのエイリアスっぽいところとそうでない所をどう区別するか、という話になります。
なお、このアプローチでは、どのような複雑なアルゴリズムであれ、究極的には、エイリアスっぽいけれど実はエイリアスじゃない本当にギザギザした所などに間違ってアンチエイリアス処理が掛かる事は防げません。 どれだけそういったものに誤って掛かる事を防ぎつつ、エイリアスにはちゃんと掛かるようなアルゴリズムにするか、というのが工夫のしどころになります。
この論文では、色が大きく変わる所をシルエットの境界とみなした時に、 エイリアスが出るのは、境界の形が、以下の三種類:
- L
- Z
- U
であろう、というのが基本的なアイデアになります。
以下の図は論文より引用:
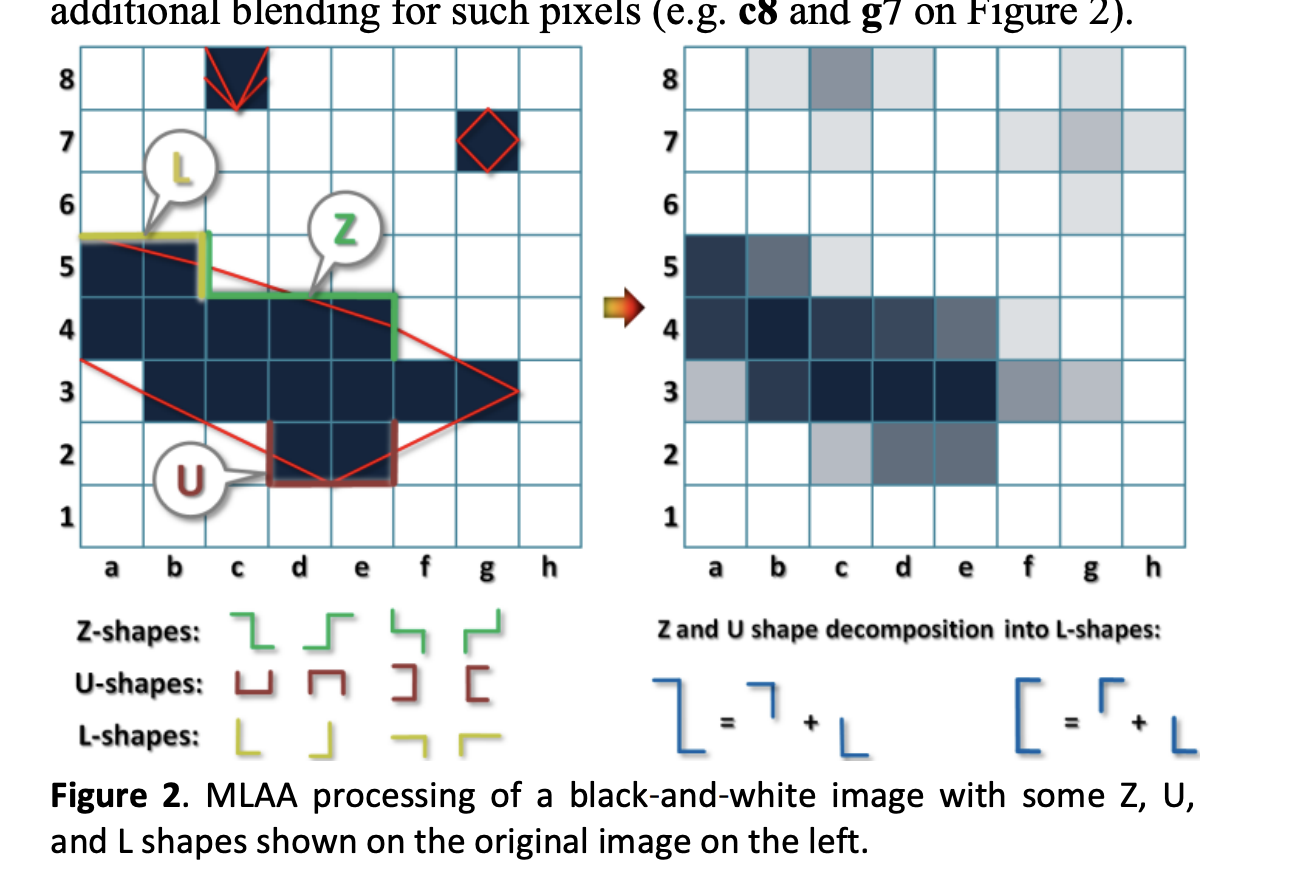
このZやUはL2つに分解出来て、結局全部Lの内側を薄める、という処理に帰着出来ます。
Lの内側はどう埋めるかというと、中点をつないだ三角形の面積を比に使ってブレンドする、という事が書いてあります。
中点なので、上の段のピクセルは一切補完されず、右側2つのピクセルも補完されません。 角の内側の狭い範囲だけ埋める感じですね。
具体的にどうやってこのLやZやUを求めていくのか、というのは実装の所で見ていきますが、基本的なアイデアはこんな所です。
このLの内側だけに限定する事で、線が全部ぼやけてしまう事なくエイリアスっぽいギザギザだけを処理する、という訳です。 当然ですがこのLにマッチしてしまえば、エイリアスじゃない所も埋められてしまうはずです。
今回の実装の、論文との差分
もともとの論文ではCPU実装なので、L字になるエッジの長さ(論文ではSeparation Lineと呼んでいる)はどこまでも探し続けるようになっていますが、 GPU実装では適当な長さで打ち切る必要があります。 とりあえず長さ7まで探してそこまでとする事にします(AMDの実装と同様)
また、カラーの場合はRGBAをそれぞれ別々に計算して、連続性のために三角形の面積を少し変える話がありますが、 RGBAを別々に計算して処理をするのはメトリックスペースでは無いので問題がある割には計算も楽では無いので、 この方法はとらず、単純にCIE XYZカラーを使う事にします。アルファも含めて、そのユークリッド距離の大きさで不連続を判断する事にします。
これはこれで問題のあるケースも考えうるとは思いますが、もともとのRGBを別々に計算するよりはおそらくマシだろう、という事で。 この辺はどこで割り切るか、という話で、GPU実装ではだいたいはそういう部分があるものです。
実際の実装: Separation Lineを求める
以下では具体的に実装を見ていきます。 まずは論文の2.1にあるfirst stepと書いてある部分の、 Separation Lineを求める、という事をやっていきたいと思います。
Separation Lineは2パスで求めます。 まず不連続な色の変化をしているピクセル間を検出します。 元論文にあるように、ピクセルの境界は2つのピクセルで共有しているため、 上下左右の4つのうち、上下のどちらか、左右のどちらか一方をすべて見ていけば十分となります。
ここでは、右と下だけ見ていく事にしましょう。なお、この場合は一番右の列と、一番下の行は調べる必要はありません。
隣接2ピクセルのSeparation Line(エッジ)の計算
まずは各ピクセルについて、その右隣りと下となりのピクセルとの色の差分を見て、閾値より大きければ1とするような計算をしてみましょう。 「隣接2ピクセル間のSeparation Line」は長いので「エッジ」と呼ぶ事にします。
let DIFF_THRESHOLD= 1.0/12.0 # これ以上RGB距離があればedgeとみなす。
# u8[right, bottom, 0, 0]を返す。
@bounds( (input_u8.extent(0)-1), (input_u8.extent(1)-1))
def edge |x, y|{
let col0 = input_u8(x, y) |> to_xyza(...)
let colRight = input_u8(x+1, y) |> to_xyza(...)
let colBottom = input_u8(x, y+1) |> to_xyza(...)
let eb = distance(colBottom, col0) > DIFF_THRESHOLD
let er = distance(colRight, col0) > DIFF_THRESHOLD
# 今の所u8v2よりu8v4の方が最適化が効くのでu8v4にしておく。
u8[er, eb, 0, 0]
}
CIE XYZカラーへの変換は以下のようにします。
let col0 = input_u8(x, y) |> to_xyza(...)
ネストが嫌でなければ、パイプライン演算子を使わずに以下のように書いても同じです。
let col0 = to_xyza(input_u8(x, y))
ではこのエッジが立つ所の色をつけてみましょう。エッジが立っているピクセルは、以下の三通りがあります。
- 右と下の両方がエッジ
- 右がエッジ
- 下がエッジ
それぞれ別の色をつけてみましょう。
let edgeEx = sampler<edge>(address=.ClampToEdge)
def result_u8 |x, y| {
let einfo = edgeEx(x, y)
ifel(einfo.x&&einfo.y,
u8[0, 0, 0xff, 0xff], #右も下もエッジ、赤
...)
elif(einfo.x,
u8[0, 0xff, 0, 0xff], #右だけエッジ、緑
...)
elif(einfo.y,
u8[0xff, 0, 0, 0xff], #下だけエッジ、青
...)
else(input_u8(x, y))
}
結果は以下です。

あってそうですが、少しわかりにくいですね。 もう少し単純な図形で試してみましょう。
以下の幾何学的な図形で試してみます。

これは以下のようになりました。

右がエッジだと緑、下がエッジだと青、両方がエッジだと赤になってそうです。
このアルゴリズムでは望ましく無さそうな場所
現時点でも、いくつかこのアルゴリズムの弱点のようなケースがわかります。 例えば以下の2つを比較してみましょう。

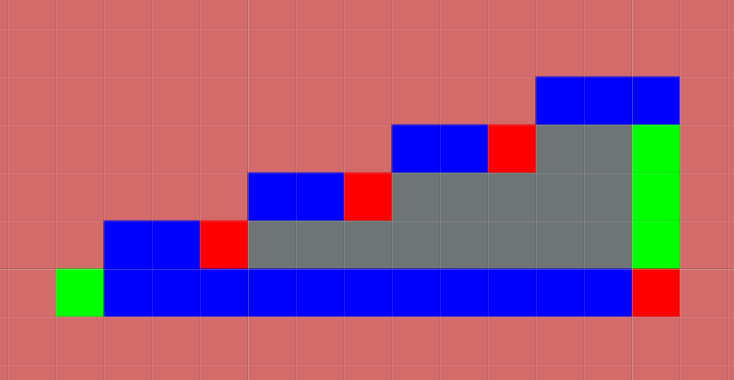
右下の角の所が赤になっています。でもここはエイリアスではなくて角ばってるだけです。 こういう角の所が少し薄められてしまう、という効果があるでしょう。
これはより改善する事が可能そうな所ですね。Lではなくもっとパターンを複雑にする事でこうしたいかにも角っぽいものは排除する、 というのはこの論文のあとに続いた関連研究で行われていたことのようです。
2パス目: 各Separation Lineに対して、それと直行しているSeparation Lineを探す
論文の「At the second step of the algorithm」から始まる所の説明の通り、 次のステップはある方向のsepration lineを見ていって、それと垂直のSeparation Lineと交わる所を探す、という事になります。
これは右、左、上、下のそれぞれに対して直行する線があって、全部同じ計算なので一気に計算出来るのですが、 かなりややこしい事になるので、単純にこのうちの一つだけ、 たとえば右に進んでいって垂直方向とぶつかる、というケースを考えていきましょう。
右に伸びるSeparation Lineが上方向のSeparation Lineとぶつかる所を探す
右に伸びる、というのは、先程作ったエッジのデータからするとbottom とrightのうちbottomの方になります。 rightじゃないのはややこしいですが、rightは右側が不連続なピクセルなので、右側を縦に走る線という事になります。

この図でいくと、横というのは赤い線をつなげたものになり、この赤の一つが前のデータでいう所のbottomになります。 ちなみに緑がrightです。
さて、垂直方向というと上方向と下方向の2つが考えられますが、 Lの内側、という事を考える場合、右のseparatin lineが下方向とぶつかるケースは、bottomではなく、一つ下のピクセルのトップと考える方が都合が良いのがあとの処理の段階で判明するので、 下方向のSeparation Lineとぶつかるのは上のエッジ、と考える事にします。
下の図では、

青のバツではなく、赤の丸の方のピクセルを考える時に処理する、という決まりとするという事です。
今回はピクセル下側のseparatin lineが右側のSeparation Lineとぶつかるケースだけを考える事にします。
各ピクセルが値を持つ
Separation Lineを求めるにあたり、どういう形で結果を持つか、という事も考えておきます。
CPUのプログラムだと、各線分ごとに長さを持つようなデータ構造をイメージすると思いますが、 GPUプログラムの場合は各ピクセルが長さのデータを持つ方が自然となります。 これはちょっと慣れていないとわかりにくいので、ここでどういうデータの持ち方になるかを考えてみましょう。
各ピクセルが、自身のbottomのエッジがどれだけ右に続くか、というデータを持つとします。 すると、図の上では以下のようになります(書いて無い所は全部0)
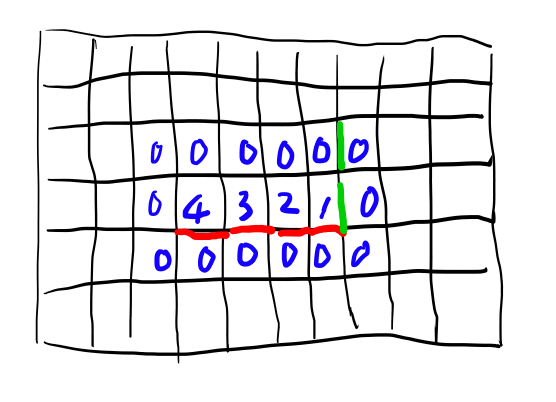
このように、4だけではなく3も2も1もある事に注意してください。
0と区別するため、自身のピクセルの右側が直行するエッジのケースは0ではなく1とする事にしましょう。
また、こういう処理をGPUでする時には固定の最大値が必要になります。 今回は8、として、SEP_MAX_LENGTHと呼ぶ事にします。
実際に水平方向のSeparation Lineの長さを求めてみよう
それでは現在のピクセルから7ピクセル横までを調べていき、bottomが続いているか、そして垂直のエッジとぶつかるかを計算してみましょう。 これにはreduceを使います。
大枠としては以下のようなコードになります。
let SEP_MAX_LENGTH = 8
# bottomを右に見ていって、右にいつぶつかるか
@bounds( (input_u8.extent(0)-1), (input_u8.extent(1)-1))
def sepLineLen1 |x, y|{
let eLenBPosi = reduce(init=0, 0..<SEP_MAX_LENGTH) |i, accm|{
#
# ここに処理を書く
# 現在のピクセルのbottomがまだあって、右がsepration lineかどうか、をチェックしてく
#
}
}
さて、このreduceの中のコメント部分を埋めていく訳ですが、 CPUでこのような処理をループで実装する場合、ループが見つからなければbreakをするのが普通です。
ですがMFGでは(というかGPUというのはそもそも)ループを途中で抜けるという事が出来ないので、 breakに相当するもう処理してないよ、という状態をフラグで表すのが良くやられる事です。 関数型言語のreduceでもたまにやりますね。 今回もそうしましょう。
ループの中のあるステップには、いくつかの状態があります。
- そもそも前のピクセルのbottmがエッジじゃなかった(処理しない)
- 既に前のピクセルまでの時点でrightのエッジに既にぶつかっている(処理しない)
- 前までのbottomがずっとエッジで、しかもまだrightのエッジにもぶつかっていない(処理する)
また、結果の長さには2つの種類がありそうです。
- 直行するエッジにぶつかって終わった
- 直行するエッジにぶつからずに終わった
2は一見すると0として良さそうに思いますが、反対側のエッジが立っている時にこの数字は意味があるので(後述)、 この種別も残す事にします。
するとフラグとしては、以下の三種類になりそうです。
- エッジにぶつかって終わった
- エッジにぶつからずに終わった
- まだ終わってない
フラグの値としては3種類ならなんでも良くて、今回のケースでは「エッジにぶつかって終わってない」が存在しないため、 1と2を2つの別のビットに割り当てる必要もありません。
単純に1のケースと2のケースをそれぞれ1, 2として、3のケースを0としましょう。
let END_NO_ORTHO = 1
let END_WITH_ORTHO = 2
let NOT_END = 0
するとreduceのinitも0ではなく、[0, 0]とフラグとlenをもたせるように変更します(これはいかにも8bitに収まりますが、そういう最適化は後ほど)
let eLenBPosi = reduce(init=[0, 0], 0..<SEP_MAX_LENGTH)
reduceのブロックの中の処理
この中は以下のような場合を考えれば良さそうでしょうか?
- A. フラグが立っている時(前のaccmをただ流すだけ)
- B. フラグが立っていない時
- B-1. bottomがエッジで無い時
- B-2. bottomがエッジの時
- B-2-1. rightがエッジでない時
- B-2-2. rightがエッジの時
言葉にすると複雑な条件ですね。恋愛サーキュレーションっぽい。 ただ一つ一つ分けて考えればそんなに複雑でも無さそう。
最初にそれぞれの条件を求めて、最後にifelで組み立てる感じで書きます。
#i, accm
let [flag, prevLen] = accm # 条件A
let [edgeR, edgeB] = edgeEx(x+i, y).xy
# 以下はそのままedgeRとedgeBでも良いけれど読みやすさのため機械的に各条件を変数にしていく
let curBottomEdge = edgeB # 条件B-2
let curRightEdge = edgeR # 条件B-2-2
ifel(flag != NOT_END, accm, ...)
elif(!curBottomEdge, [END_NO_ORTHO, prevLen], ...) # B-1, 垂直のエッジとぶつからずにbottomの端まで来た、一つ前までの長さとして終了フラグをセット
elif(curRightEdge, [END_WITH_ORTHO, prevLen+1], ...) # B-2-2
else([NOT_END, prevLen+1]) # B-2-1
ではこれをデバッグ表示してみましょう。
let SEP_MAX_LENGTH = 8
# bottomを右に見ていって、右にいつぶつかるか
@bounds( (input_u8.extent(0)-1), (input_u8.extent(1)-1))
def sepLineLen1 |x, y|{
let eLenBPosi = reduce(init=[0, 0], 0..<SEP_MAX_LENGTH) |i, accm|{
let [flag, prevLen] = accm # 条件A
let [edgeR, edgeB] = edgeEx(x+i, y).xy
# 以下はそのままedgeRとedgeBでも良いけれど読みやすさのため機械的に各条件を変数にしていく
let curBottomEdge = edgeB # 条件B-2
let curRightEdge = edgeR # 条件B-2-2
ifel(flag != NOT_END, accm, ...)
elif(!curBottomEdge, [END_NO_ORTHO, prevLen], ...) # B-1, 垂直のエッジとぶつからずにbottomの端まで来た、一つ前までの長さとして終了フラグをセット
elif(curRightEdge, [END_WITH_ORTHO, prevLen+1], ...) # B-2-2
else([NOT_END, prevLen+1]) # B-2-1
}
eLenBPosi
}
let sepLineLen1Ex = sampler<sepLineLen1>(address=.ClampToBorderValue, border_value=[0, 0])
def result_u8 |x, y| {
let [flag, sepLen0] = sepLineLen1Ex(x, y)
# 直行しているのにぶつからなかった時はゼロとしてデバッグ表示してみる。
let sepLen = ifel(flag == END_WITH_ORTHO, sepLen0, 0)
# sepLenは0から8。
# この結果をR成分としてデバッグ表示してみる。
# 0.0〜1.0を8等分してガンマ補正する。
# u8に戻すのは面倒なので
let r = 1.0*f32(sepLen)/f32(SEP_MAX_LENGTH)
let debVal = [0.0, 0.0, r, 1.0] |> lbgra_to_u8color(...)
ifel(sepLen > 0, debVal, input_u8(x, y))
}
すると以下のようになりました。

灰色のところの下辺の左側が赤くなっていない(最大長より遠くにエッジがある場合はL字の一部とはみなさない)所や、 黄色の段々の一番右側は赤くなっていない(右にいっても画面端まで行ってしまって直行するエッジにぶつからない)所などに注目してください。
Bottomの左側の処理をする
正の方向の処理が終わったので負の方向も考えてみます。 curとortho以外の処理はほとんど同じになるので、 一回dupして書き直したあとに、共通化出来そうな事を考えて一つにしてしまいます。
この時、フラグの計算とlenの計算を分けた方がベクトライズが少し減って理解しやすいので、 この2つの計算を分ける事にします。
すると、以下のようになりました。
let eLenB = reduce(init=[0, 0, 0, 0], 0..<SEP_MAX_LENGTH) |i, accm|{
let flag = accm.xy
let prevLen = accm.zw
# この辺が毎回変わる
let [ortho0, cur0] = edgeEx(x+i, y).xy |> i32(...)
let [_, cur1] = edgeEx(x-i, y).xy |> i32(...)
let [ortho1, _] = edgeEx(x-i-1, y).xy |> i32(...)
let cur = [cur0, cur1]
let ortho = [ortho0, ortho1]
let newF = ifel(flag != NOT_END, flag, ...)
elif((!cur), vec2(END_NO_ORTHO), ...)
elif(ortho, vec2(END_WITH_ORTHO), vec2(NOT_END))
let newL = ifel(flag != NOT_END, prevLen, ...)
elif(!cur, prevLen, ...)
else(prevLen+1)
[*newF, *newL]
}
newFとifelの所、つまり以下は、ベクトル演算になっています。
let newF = ifel(flag != NOT_END, flag, ...)
elif((!cur), vec2(END_NO_ORTHO), ...)
elif(ortho, vec2(END_WITH_ORTHO), vec2(NOT_END))
let newL = ifel(flag != NOT_END, prevLen, ...)
elif(!cur, prevLen, ...)
else(prevLen+1)
flagやcurなどの変数はすべて2次元になっていて、それぞれの次元を一気に計算しています。 newFのvec2(END_NO_ORTHO)はcurによっては片方だけが採用される事に注意してください。
この手のコードはシェーダーやRやMatlabなどの言語に慣れていないと少し驚くかもしれません。 MFGでifが文で無いのはこの辺との相性の良さが理由でもあります。
復数の処理を一つにまとめるべきか検討
さて、これとほぼ同じような作業をあと6つやる必要があります。 つまり以下です。
- bottomを右に伸ばしていってrightとぶつかるか?(<ーこれを既にやった)
- bottomを左に伸ばしていってleftとぶつかるか?(<ーこれを既にやった)
- topを右に伸ばしていってrightとぶつかるか?
- topを左に伸ばしていってleftとぶつかるか?
- rightを上に伸ばしていってtopとぶつかるか?
- rightを下に伸ばしていってbottomとぶつかるか?
- leftを上に伸ばしていってtopとぶつかるか?
- leftを下に伸ばしていってbottomとぶつかるか?
たぶん頑張ればこれらはすべて一つのreduceで処理出来そうです。 一方でそれはかなり複雑になりそう。 効率的には一つでやるのが一番良くなるとはいえ、メモリアクセスの回数はほとんど変わらないので、速度的には8個コピペして変更してもたぶん大差無い。
それよりも8個も似た重複があるのはコードの読みやすさや保守性の面できつい。 ただ、どれも基本的にはかなり似ていてちょっとだけ違うのだけれど、 そのちょっと違う違い方がそれぞれ違うので、全部共通の部分は実はかなり少ない。 いい感じに共通部分が多いものだけまとめる、というのは難しい。
おそらく取りうる選択肢は以下のどちらかと思います。
- 諦めて全部一つのreduceにまとめて複雑なコードを頑張る
- 適当な4つずつの2グループに分けてdup一回の処理にする
どちらも試しましたが、どっちもいまいちな感じになるので、どっちでも良さそうです。 今回は1の諦めて全部一つにまとめる、という方針でいきましょう。
世の中のシェーダーのコードはだいたいぜんぶ一つにまとめて複雑な暗号的なコードを受け入れる傾向が強いですね。
基本的には上から順番に一つdupして実装してみて、共通化出来ないか考える、を繰り返せば良さそう。
だいたいはcurとorthoを作る所だけが違っていて、他はだいたい同じコードとなります。
同じように全部まとめてしまうと、以下のようになります。
# i32を4ビットずつに分けてビッグエンディアンの8次元タプルとして返す。
fn split8 |v: i32| {
let e1 = v&0xf
let e2 = (v>>4)&0xf
let e3 = (v>>8)&0xf
let e4 = (v>>12)&0xf
let e5 = (v>>16)&0xf
let e6 = (v>>20)&0xf
let e7 = (v>>24)&0xf
let e8 = (v>>28)&0xf
i32[e8, e7, e6, e5, e4, e3, e2, e1]
}
# ベクトルの各要素を0xfまでの数値とみなして32ビットにパックする。(結果はi32)
# 並び順はsplit8と同じで、v2が上位ビット。
fn merge8 |v2: i32v4, v1: i32v4| {
let [e4, e3, e2, e1] = v1
let [e8, e7, e6, e5] = v2
(e8 << 28) | (e7 << 24) | (e6 << 20) | (e5 <<16 ) | (e4 << 12) | (e3 << 8) | (e2 << 4) | e1
}
let SEP_MAX_LENGTH = 8
let END_NO_ORTHO = 1
let END_WITH_ORTHO = 2
let NOT_END = 0
# vec8は無いのでvec4を2つ並べてspreadする。
let END_NO_ORTHO8 = [*vec4(END_NO_ORTHO), *vec4(END_NO_ORTHO)]
let END_WITH_ORTHO8 = [*vec4(END_WITH_ORTHO), *vec4(END_WITH_ORTHO)]
let NOT_END8 = [*vec4(NOT_END), *vec4(NOT_END)]
# Bottom, Right, Top, Left. Pos Neg each.
@bounds( (input_u8.extent(0)-1), (input_u8.extent(1)-1))
def sepLineLen |x, y|{
let eLenBRTL = reduce(init=[0, 0], 0..<SEP_MAX_LENGTH) |i, accm|{
# v8, bpos, bneg, rpos, rneg, toppos, topneg, leftpos, leftneg
let flag = split8(accm.x)
let prevLen = split8(accm.y)
let [ortho0, cur0] = edgeEx(x+i, y).xy |> i32(...)
let [_, cur1] = edgeEx(x-i, y).xy |> i32(...)
let [ortho1, _] = edgeEx(x-i-1, y).xy |> i32(...)
let [cur2, ortho2] = edgeEx(x, y+i).xy |> i32(...)
let [cur3, _] = edgeEx(x, y-i).xy |> i32(...)
let [_, ortho3] = edgeEx(x, y-i-1).xy |> i32(...)
# Top
let [_, cur4] = edgeEx(x+i, y-1).xy |> i32(...)
# Topと直行するrightは一つ下
# 以下だが、これはortho0と同じ
# let [ortho4, _] = edgeEx(x+i, y).xy |> i32(...)
let ortho4 = ortho0
# Top Negative方向
let [_, cur5] = edgeEx(x-i, y-1).xy |> i32(...)
# これはortho1と同じ
# let [ortho5, _] = edgeEx(x-i-1, y).xy |> i32(...)
let ortho5 = ortho1
# Left
let [cur6, _] = edgeEx(x-1, y+i).xy |> i32(...)
# Leftと直行するbottomは一つ右隣り、これはortho2と同じ
# let [_, ortho6] = edgeEx(x, y+i).xy |> i32(...)
let ortho6 = ortho2
# Left neg(上方向)
let [cur7, _] = edgeEx(x-1, y-i).xy |> i32(...)
# 以下はortho3と同じ
# let [_, ortho7] = edgeEx(x, y-i-1).xy |> i32(...)
let ortho7 = ortho3
let cur = [cur0, cur1, cur2, cur3, cur4, cur5, cur6, cur7]
let ortho = [ortho0, ortho1, ortho2, ortho3, ortho4, ortho5, ortho6, ortho7]
let newF = ifel(flag != NOT_END, flag, ...)
elif((!cur), END_NO_ORTHO8, ...)
elif(ortho, END_WITH_ORTHO8, NOT_END8)
let newL = ifel(flag != NOT_END, prevLen, ...)
elif(!cur, prevLen, ...)
else(prevLen+1)
# 8次元はベクトルとして扱えないので4次元ごとにバラす
let newF_Merge = merge8([newF.0, newF.1, newF.2, newF.3], [newF.4, newF.5, newF.6, newF.7])
let newL_Merge = merge8([newL.0, newL.1, newL.2, newL.3], [newL.4, newL.5, newL.6, newL.7])
[newF_Merge, newL_Merge]
}
eLenBRTL
}
これを解読するのは大変ですね。 結局は
- 下の正負
- 右の正負
- 上の正負
- 左の正負
の8通りについて、今の位置のエッジ(curXX)とそれと直行するエッジ(orthoXX)を求めて、あとは同じ計算となります。 newFとnewLの計算が一つの時と全く同じ形なのは、ベクトル演算の威力が出る所ですね。
MFGの多くの機能(swizzle演算子など)が4要素までを想定していて8要素とか16要素だとあまり取り回しが良くないので、 復数の要素を一つのi32にパックしています。 長さは最大で8なので4bitにおさまるため、i32に8個詰めています。
# i32を4ビットずつに分けてビッグエンディアンの8次元タプルとして返す。
fn split8 |v: i32| {
let e1 = v&0xf
let e2 = (v>>4)&0xf
let e3 = (v>>8)&0xf
let e4 = (v>>12)&0xf
let e5 = (v>>16)&0xf
let e6 = (v>>20)&0xf
let e7 = (v>>24)&0xf
let e8 = (v>>28)&0xf
i32[e8, e7, e6, e5, e4, e3, e2, e1]
}
# ベクトルの各要素を0xfまでの数値とみなして32ビットにパックする。(結果はi32)
# 並び順はsplit8と同じで、v2が上位ビット。
fn merge8 |v2: i32v4, v1: i32v4| {
let [e4, e3, e2, e1] = v1
let [e8, e7, e6, e5] = v2
(e8 << 28) | (e7 << 24) | (e6 << 20) | (e5 <<16 ) | (e4 << 12) | (e3 << 8) | (e2 << 4) | e1
}
ここではユーザー定義関数を使っています。
リファレンス: ユーザー定義関数と組み込み関数#ユーザー定義関数
MFGでは中間テンソルとブロック引数でだいたいは用が足りるので簡単なフィルタではあまり出番はありませんが、 こういう用途ではユーザー定義関数は便利ですね。
merge8の方は、本来はi32v8としたい所ですが、ベクトルは4要素まででi32v8という型は存在しないため、 i32v4を2つ渡す事にしています。
エンディアンはバイナリ処理に慣れているとリトルエンディアンで統一した方が読みやすい人も多いと思いますが、 今回はビッグエンディアンで並べています。
今回実装したコード全体
最後に今回実装したコードの全体を載せておきます。 結果はMFGStudioのnon_aa_color_shape.mdzに適用して確認すると分かりやすいと思います。
@title "MLAA Separation Line"
let DIFF_THRESHOLD= 1.0/12.0 # これ以上RGB距離があればedgeとみなす。
# u8[right, bottom, 0, 0]を返す。
@bounds( (input_u8.extent(0)-1), (input_u8.extent(1)-1))
def edge |x, y|{
let col0 = input_u8(x, y) |> to_xyza(...)
let colRight = input_u8(x+1, y) |> to_xyza(...)
let colBottom = input_u8(x, y+1) |> to_xyza(...)
let eb = distance(colBottom, col0) > DIFF_THRESHOLD
let er = distance(colRight, col0) > DIFF_THRESHOLD
# 今の所u8v2よりu8v4の方が最適化が効くのでu8v4にしておく。
u8[er, eb, 0, 0]
}
let edgeEx = sampler<edge>(address=.ClampToEdge)
# i32を4ビットずつに分けてビッグエンディアンの8次元タプルとして返す。
fn split8 |v: i32| {
let e1 = v&0xf
let e2 = (v>>4)&0xf
let e3 = (v>>8)&0xf
let e4 = (v>>12)&0xf
let e5 = (v>>16)&0xf
let e6 = (v>>20)&0xf
let e7 = (v>>24)&0xf
let e8 = (v>>28)&0xf
i32[e8, e7, e6, e5, e4, e3, e2, e1]
}
# ベクトルの各要素を0xfまでの数値とみなして32ビットにパックする。(結果はi32)
# 並び順はsplit8と同じで、v2が上位ビット。
fn merge8 |v2: i32v4, v1: i32v4| {
let [e4, e3, e2, e1] = v1
let [e8, e7, e6, e5] = v2
(e8 << 28) | (e7 << 24) | (e6 << 20) | (e5 <<16 ) | (e4 << 12) | (e3 << 8) | (e2 << 4) | e1
}
let SEP_MAX_LENGTH = 8
let END_NO_ORTHO = 1
let END_WITH_ORTHO = 2
let NOT_END = 0
# vec8は無いのでvec4を2つ並べてspreadする。
let END_NO_ORTHO8 = [*vec4(END_NO_ORTHO), *vec4(END_NO_ORTHO)]
let END_WITH_ORTHO8 = [*vec4(END_WITH_ORTHO), *vec4(END_WITH_ORTHO)]
let NOT_END8 = [*vec4(NOT_END), *vec4(NOT_END)]
@bounds( (input_u8.extent(0)-1), (input_u8.extent(1)-1))
def sepLineLen |x, y|{
let eLenBRTL = reduce(init=[0, 0], 0..<SEP_MAX_LENGTH) |i, accm|{
# v8, bpos, bneg, rpos, rneg, toppos, topneg, leftpos, leftneg
let flag = split8(accm.x)
let prevLen = split8(accm.y)
let [ortho0, cur0] = edgeEx(x+i, y).xy |> i32(...)
let [_, cur1] = edgeEx(x-i, y).xy |> i32(...)
let [ortho1, _] = edgeEx(x-i-1, y).xy |> i32(...)
let [cur2, ortho2] = edgeEx(x, y+i).xy |> i32(...)
let [cur3, _] = edgeEx(x, y-i).xy |> i32(...)
let [_, ortho3] = edgeEx(x, y-i-1).xy |> i32(...)
# Top
let [_, cur4] = edgeEx(x+i, y-1).xy |> i32(...)
# Topと直行するrightは一つ下
# 以下だが、これはortho0と同じ
# let [ortho4, _] = edgeEx(x+i, y).xy |> i32(...)
let ortho4 = ortho0
# Top Negative方向
let [_, cur5] = edgeEx(x-i, y-1).xy |> i32(...)
# これはortho1と同じ
# let [ortho5, _] = edgeEx(x-i-1, y).xy |> i32(...)
let ortho5 = ortho1
# Left
let [cur6, _] = edgeEx(x-1, y+i).xy |> i32(...)
# Leftと直行するbottomは一つ右隣り、これはortho2と同じ
# let [_, ortho6] = edgeEx(x, y+i).xy |> i32(...)
let ortho6 = ortho2
# Left neg(上方向)
let [cur7, _] = edgeEx(x-1, y-i).xy |> i32(...)
# 以下はortho3と同じ
# let [_, ortho7] = edgeEx(x, y-i-1).xy |> i32(...)
let ortho7 = ortho3
let cur = [cur0, cur1, cur2, cur3, cur4, cur5, cur6, cur7]
let ortho = [ortho0, ortho1, ortho2, ortho3, ortho4, ortho5, ortho6, ortho7]
let newF = ifel(flag != NOT_END, flag, ...)
elif((!cur), END_NO_ORTHO8, ...)
elif(ortho, END_WITH_ORTHO8, NOT_END8)
let newL = ifel(flag != NOT_END, prevLen, ...)
elif(!cur, prevLen, ...)
else(prevLen+1)
# 8次元はベクトルとして扱えないので4次元ごとにバラす
let newF_Merge = merge8([newF.0, newF.1, newF.2, newF.3], [newF.4, newF.5, newF.6, newF.7])
let newL_Merge = merge8([newL.0, newL.1, newL.2, newL.3], [newL.4, newL.5, newL.6, newL.7])
[newF_Merge, newL_Merge]
}
eLenBRTL
}
let sepLineLenEx = sampler<sepLineLen>(address=.ClampToBorderValue, border_value=[0, 0])
def result_u8 |x, y| {
let [flagM, lenM] = sepLineLenEx(x, y)
let flag = split8(flagM)
let sepLenO = split8(lenM)
# テスト確認用
let sepLen = ifel(flag.z == END_WITH_ORTHO, sepLenO.z, 0)
# sepLenは0から8。
# この結果をR成分としてデバッグ表示してみる。
# 0.0〜1.0を8等分してガンマ補正する。
# u8に戻すのは面倒なので
let r = 1.0*f32(sepLen)/f32(SEP_MAX_LENGTH)
let debVal = [0.0, 0.0, r, 1.0] |> lbgra_to_u8color(...)
ifel(sepLen > 0, debVal, input_u8(x, y))
}
前編まとめ
- MLAAは色の不連続な変化の形状に着目してエイリアスっぽい所を探すアンチエイリアスの手法だよ
- 不連続なピクセル境界をSeparation Lineと呼ぶ事にするよ
- Separation Lineとその直行するSeparation Lineの長さを求めたよ
- 結果は各ピクセルが持つ所がGPUのプログラム的だね
後編では、今回作ったSepration Lineの長さのデータを使って、どうアンチエイリアスを実装するかを見ていきます。