MFGのクリスタライズフィルタの修正

クリスタライズフィルタの端の処理がバグってるよ！と言われる。

確かに。という事でこれを直す過程をブログにしてみようと思う。

今回もMFGStudioで開発していく。

開発時のメモが以下にある

クリスタライズフィルタを作った当時の開発過程は、以下にノートがある。

MFG/docs/ja/study/Crystallize.md at main · karino2/MFG

ただ、上記ドキュメントは試行錯誤しながら書いているので、 結論が分かった今もう一度整理してみると、もう少しわかりやすくなるだろう。

バグがあるという事は上記のドキュメントに間違いもあるはずなので、 ドキュメントも整理して書き直してみるのは良いアイデアな気がする。 いい機会なのでデバッグの目的も兼ねてもう一度このフィルターを、このブログ記事で振り返る事にする。

クリスタライズフィルタは何をしているか？

バグ修正の前に、クリスタライスフィルタは何をしているか、という事から。 これはこんな感じのフィルタ作れない？と言われて適当に自分が考えたアルゴリズムなので、原典とかは無い。

目的の効果は、形はボロノイ図っぽいな、と思った。ボロノイ図 - Wikipedia

けれどボロノイ図は普通はCPU的なアルゴリズムだし、 そもそも一般のボロノイ図はクリスタルっぽくないケースも出てくるだろうから、 むしろ母点はランダムでは無くある程度の制約がある方が良さそう。

という事で格子の点を適当にランダムに動かした、perlinノイズと同じようなものに対してのボロノイ図はどうだろう？

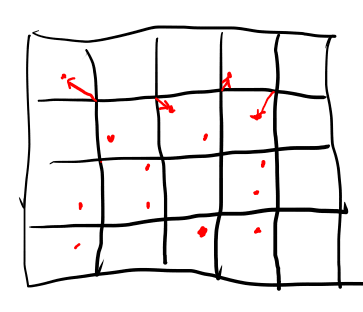
ランダムな度合いは+-0.5の範囲にしておけば、隣の点を追い越す事はたぶん無い。 という事で、任意の点は近隣の4点を調べればどこが一番近い母点かを確定させる事が出来るだろう。（あとでちゃんと考えたら12点考えないと駄目だった。後述）

これを簡易ボロノイ図、と呼ぶ事にする。

こうしてボロノイ図の領域を決めたら、その中をモザイクのように色を平均し、それを使えばいいんじゃないか。

母点となるランダムな格子を描いてみる（GPU的に考える必要性）

では簡易ボロノイ図を描くために、ランダムな格子点を描いてみよう。

適当なインターバルで分割した格子の交点をランダムにずらした点を打ってみよう。 これはランダムにずらすオフセットをテンソルにして、各交点を描く時にこのオフセットだけずらすのが良さそう（パーリンノイズではそうしている）。

描いてみよう。

ここでGPUとCPUの違いが出てくる所で、点を計算してその点を打つ、という風にはプログラム出来ない。 そうでは無く、ある点があった時に、それが目的の点に近いか？という風にプログラムしなくてはならない。

ある点があった時に格子点からずらした点のそばなのかどうかを考えるには、 直感的にはある点の周囲4つの格子を考えれば良さそうだが、良く考えたら4点よりも外が近くなる可能性がある事に気づいた。

つまり斜めは \(\sqrt{2} \times 0.5\) になってしまうため、0.5より大きく（遠く）なりうる。

というのを少し考えた所、以下の格子点から生まれた点を探せば十分っぽい、という結論になりました。

三角が考えているx, yでバツが格子点。 斜めの4隅は不要だけれど、プログラム的には調べた方がコードは簡単なので調べてしまう事にしましょう。

という事で前後の合計4つの点を縦横に見ていけばいいので、0..<4でrsumしてみよう。

@title "ランダムな格子点"

@param_i32 GRID_INTERVAL(SLIDER, label="Grid Size", min=10, max=256, init=50)
@param_f32 STRENGTH(SLIDER, label="Random Strength", min=0.1, max=1.0, init=1.0)

let [GRID_WIDTH, GRID_HEIGHT] = (input_u8.extent() -1)/GRID_INTERVAL + 1

@bounds(GRID_WIDTH, GRID_HEIGHT)
def gridOffset |x, y|{
  STRENGTH*[rand()-0.5, rand()-0.5]
}

let goffEx = sampler<gridOffset>(address=.ClampToBorderValue, border_value=[0.0, 0.0])

def result_u8 |x, y| {
  let go_xy = [x, y]/GRID_INTERVAL # x y of grid coordinate, upper left

  let nearest = reduce(init=[0, 0, 999999.0], 0..<4, 0..<4) |rx, ry, accm| {
    let gxy = go_xy + [-1, -1] + [rx, ry]
    let ggxy = gxy*GRID_INTERVAL + i32(goffEx(*gxy)*GRID_INTERVAL) # global coordinate
    let d = distance(f32([x, y]), f32(ggxy))
    ifel(d <accm.z, 
        [gxy.x, gxy.y, d],
        accm
    )
  }
  let d = nearest.z
  ifel( d < 5.0, u8[0, 0, 0xff, 0xff], u8(vec4(0)) )
}

格子も書かないと良く分からないな。こういう時は、２つのフィルタを順番に適用して、２つ目は目的の点以外はinput_u8を返すようにするとデバッグ出来る。 現状は一つのプロジェクトにmfgを追加する方法はMFGStudioには無いが、コンソールからtouchで作る。

@title "格子を描く"

@param_i32 GRID_INTERVAL(SLIDER, label="Grid Size", min=10, max=256, init=150)

def result_u8 |x, y| {
  let go_xy = [x, y]/GRID_INTERVAL # x y of grid coordinate, upper left
  let gxy = f32(go_xy*GRID_INTERVAL)
  let d = min(*abs(f32[x, y] - gxy))

  ifel( d < 5.0, u8[0, 0, 0xff, 0xff], u8(vec4(0)) )
}

dを求める所はabsをspreadしてminをとる、というちょっとエレガントなコードになってますね。こういうのはMFG力が出る所。 ついでにGRID_INTERVALは150くらいにしておきました。

これを実行して、その後に黒の点を打つフィルタを実行しましょう。 さっきのランダムな格子点の最後を以下のように変えます。

  ifel( d < 10.0, u8[0, 0, 0, 0xff], input_u8(x, y) )

黒にして、elseの方をinputにかえて、さらに点の大きさを倍くらいにしてみました（見づらかったので）。 フィルタを順番に適用すると以下のようになります。

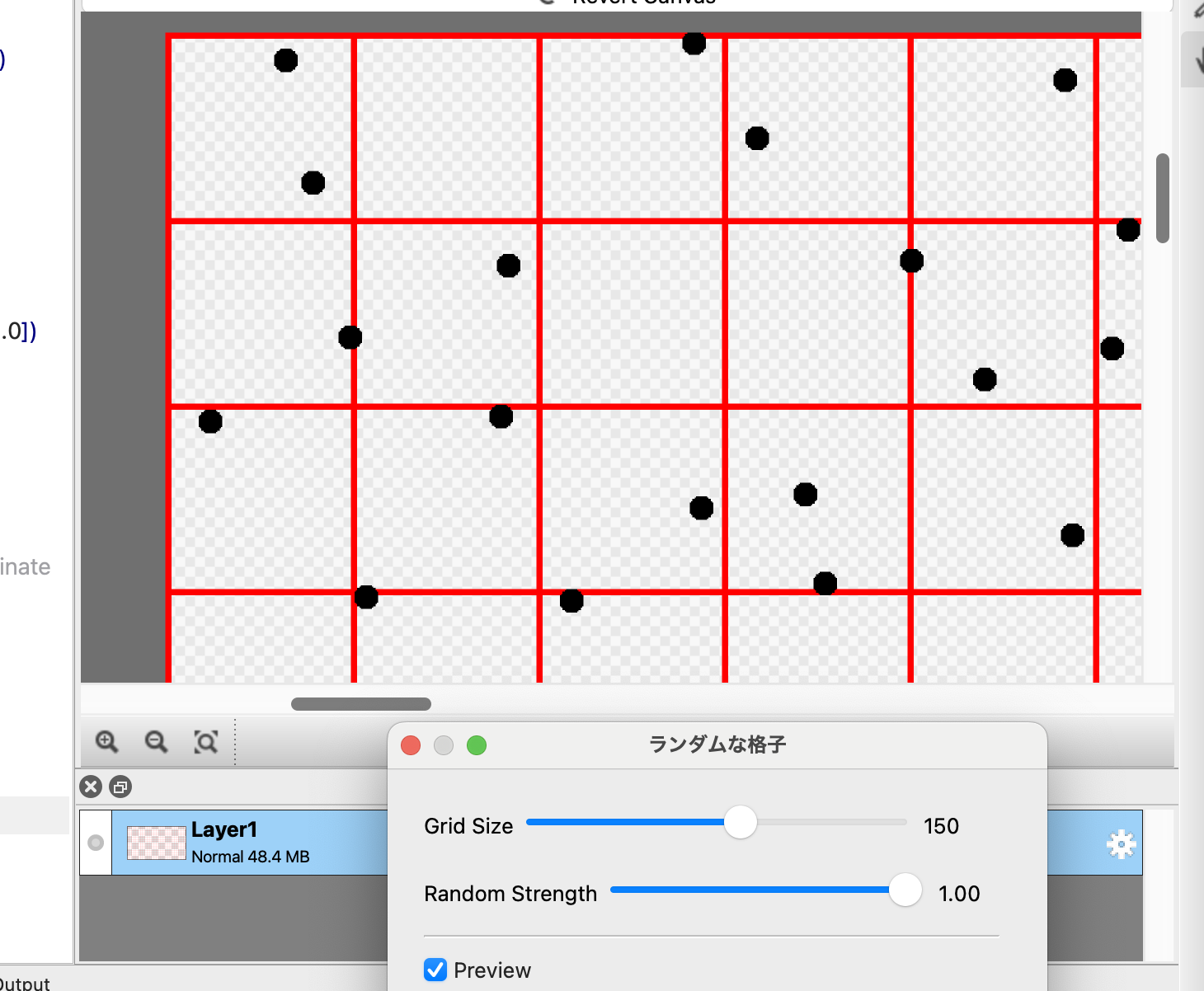
バグとしてはこれの画面端の所の処理が間違っていて母点がうまく行ってないのかなぁ、と予想する。 下の端を見ると以下。

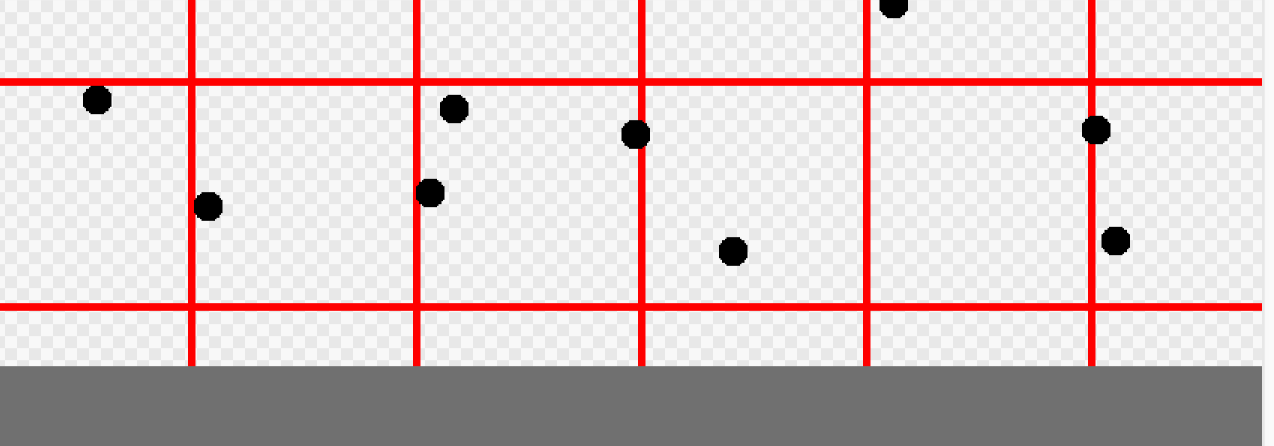
なんとなく最後のセルの母点は描けていない気がしますね。

簡易ボロノイ図を描いてみる

とりあえずバグはおいといて、これを元にボロノイ図を描いてみます。

前のプログラムのresult_u8の前半部分である、 最近傍の母点とその距離をnnというテンソルにしておこう（x, yはi32の座標でzはf32の距離）。

@bounds(input_u8.extent(0), input_u8.extent(1))
def nn |x, y| {
  let go_xy = [x, y]/GRID_INTERVAL # x y of grid coordinate, upper left

  let nearest = reduce(init=[0, 0, 999999.0], 0..<4, 0..<4) |rx, ry, accm| {
    let gxy = go_xy + [-1, -1] + [rx, ry]
    let ggxy = gxy*GRID_INTERVAL + i32(goffEx(*gxy)*GRID_INTERVAL) # global coordinate
    let d = distance(f32([x, y]), f32(ggxy))
    ifel(d <accm.z, 
        [gxy.x, gxy.y, d],
        accm
    )
  }
  nearest
}

def result_u8 |x, y| {
  let nearest = nn(x, y)
  let d = nearest.z
  ifel( d < 10.0, u8[0, 0, 0, 0xff], input_u8(x, y) )
}

nnはピクセルの数だけ作られてしまうので結構無駄ではありますが、このくらいの無駄はGPUプログラムでは良くある範囲です。 毎回result_u8で全部計算する方がパフォーマンスもメモリもたぶん良いですが、コードの可読性や保守性とのトレードオフなので、 まずは開発しやすさを優先する方がいいでしょう。

そしてもよりのnnの座標に応じて適当に色分けします。 真面目にやるなら4色問題とかそういう話になりますが、 母点のx, yから一意に、隣同士が大きく異なりそうな色を適当に振ればここでの目的としては十分でしょう。

def result_u8 |x, y| {
  let nearest = nn(x, y)
  let d = nearest.z

  let bxy = f32(nearest.xy)
  # 数字は適当
  let b = dot(bxy, f32[123456, 7891234])/255
  let g = dot(bxy, f32[567891, 23456])/255
  let r = dot(bxy, f32[78912, 34567])/255
  let col = u8[b, g, r, 255]
  ifel( d < 10.0, u8[0, 0, 0, 0xff], col )
}

最近傍の母点のxyに応じて適当ないろを作り、母点は黒で表示しています。

割と良さそうですね。 格子点の付近という簡易的なボロノイ図ですが、意外と形も多様で良さそうです。

一番下の境界もおかしい事は起きて無さそうに見えます。

ボロノイ図の領域を平均した色で置き換える

母点ごとに、上記の同じ色の領域をinput_u8を平均して得られる色を求めて母点にassignしたい。 これもGPU的に解く方法を考えないといけません。

感覚的には母点ごとのテンソルで、母点から候補になりそうな最大の範囲のピクセルを見て平均をとってやれば良さそう。

母点ごとに色をassignしてみる（バグ発見！）

まずは母点にさっきと同様の式で母点の座標に応じた色をassignして表示するようにプログラムを変えてみよう。 こんな感じか？

@bounds(GRID_WIDTH, GRID_HEIGHT)
def gridCol |x, y|{
  let bxy = f32[x, y]
  let b = dot(bxy, [123456.0, 7891234.0])/255
  let g = dot(bxy, [567891.0, 23456.0])/255
  let r = dot(bxy, [78912.0, 34567.0])/255
  u8[b, g, r, 255]
}

これでresult_u8を以下に変える。

  let col = gridCol(*nearest.xy)

すると以下のようになった。

おぉ、端がおかしいのが再現した。nearest.xyから直接色を計算していた時には再現しなかったので、 ようするにこのgridColの外側になってしまっているっぽいな。

ClampToEdgeにしてみよう。

let gridColEx = sampler<gridCol>(address=.ClampToEdge)

するとこうなった。

期待している結果とは違うが、やはり端のアクセスになってしまっているのは間違い無さそう。

最近傍の母点のxyの可能な範囲を考える

さて、GRID_WIDTHとGRID_HEIGHTで色をassignしたのが足りてないので、これに2とか適当に足せば良さそうだが、 マイナスの方も同じような事が起きているかもしれないので、真面目に範囲を考える。

nearestのxyを出しているのは以下だ。

let go_xy = [x, y]/GRID_INTERVAL # x y of grid coordinate, upper left

let nearest = reduce(init=[0, 0, 999999.0], 0..<4, 0..<4) |rx, ry, accm| {
  let gxy = go_xy + [-1, -1] + [rx, ry]
  let ggxy = gxy*GRID_INTERVAL + i32(goffEx(*gxy)*GRID_INTERVAL) # global coordinate
  let d = distance(f32([x, y]), f32(ggxy))
  ifel(d <accm.z, 
      [gxy.x, gxy.y, d],
      accm
  )
}

この go_xy はグリッドの格子点を左上を0として何番目かをそれぞれ表す。これを格子座標系と呼ぶ事にする。 次のgxyも格子座標系で、これは、

\[(-1, -1) \leq gxy \leq (gx_{max}+2, gy_{max}+2)\]

となっている。 母点はこの範囲になりうるので、色の平均もこの範囲で求めてやる必要があるか。

@bounds(GRID_WIDTH+3, GRID_HEIGHT+3)
def gridCol |x, y|{
  let bxy = f32[x, y]
  let b = dot(bxy, [123456.0, 7891234.0])/255
  let g = dot(bxy, [567891.0, 23456.0])/255
  let r = dot(bxy, [78912.0, 34567.0])/255
  u8[b, g, r, 255]
}

こうして、さらに-1からなので1を足してやれば、

  let col = gridCol(*(nearest.xy+[1, 1]))

こうなった。

よしよし、正しくなったね。

同じ母点の領域の最大範囲

では後はgridColを、座標から計算した色では無く同じ母点になる範囲のinput_u8の色の平均で置き換えてやれば完成だ。

ただCPUのケースと違って、input_u8の範囲をなめてgridColを作る、という事は出来ない。 gridColの範囲をなめて、その各格子点である程度の範囲を調べて、そのある程度の範囲がそれぞれオーバーラップする事で全体を覆う必要がある。

一つの格子点が担当すべき、最大の範囲はどのくらいだろうか？ボロノイ図を眺めていると、周辺の母点より外側になる事は無いので、 自分を中心に3x3の範囲くらいを見れば十分そうには見える。

以前開発した時に同じ事を考えていて、開発時のメモで、以下のように言っている。

「ある母点の足し合わせる範囲の最大の範囲を考えたい。 ある母点がランダムで動く範囲は最大で0.5だ。その一番動いたところでもっとも遠い最近接点の可能性を考えると、 周囲の8個の母点をそれぞれ0.5 intervalだけ広げた矩形になる、かな。」

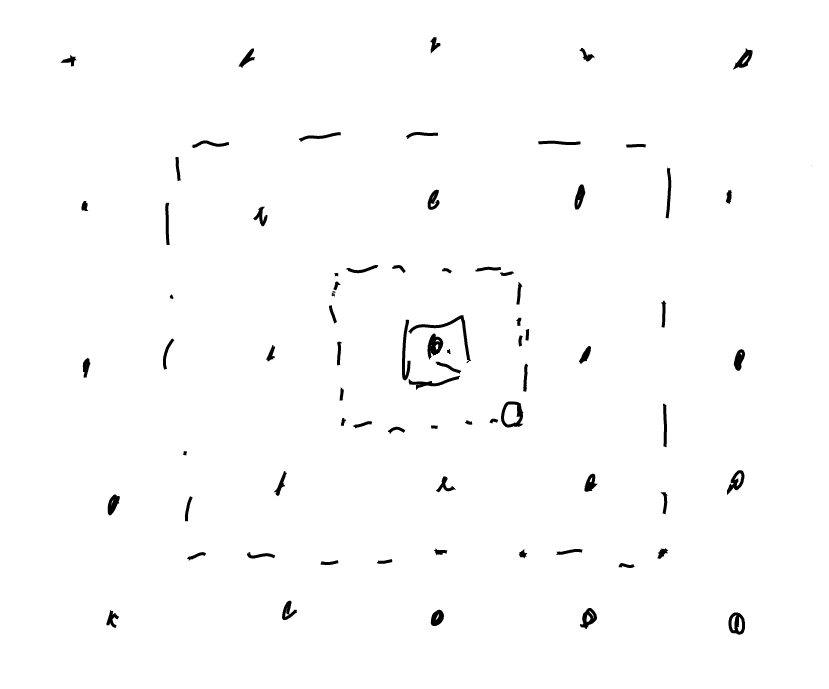
これはさきほど眺めた3x3くらいの範囲でだいたい十分だろう、という直観とも一致してそう。

上のメモでは、「-1.5 gridIntervalから +1.5 gridIntervalの範囲を計算すればいい」と結論づけている。正しそうに見えるのでこれで計算してみる。

各母点で担当候補の範囲を全部なめるコードは以下のようになるだろう。

@bounds(GRID_WIDTH+3, GRID_HEIGHT+3)
def gridCol |x, y|{
   # x, yは+1しているので-1して格子座標系に戻す。
   let gxy = [x, y] - 1

   # 格子のスクリーン座標での値
   let gs_xy0 =  gxy* GRID_INTERVAL

   # 一つの母点が担当すべき最大範囲
   let candW = 3*GRID_INTERVAL
   let [sb, sg, sr, sa, count] = rsum(0..<candW, 0..<candW) |rx, ry|{
      # 担当範囲のスクリーン座標でのピクセル位置
      let sxy = gs_xy0+[rx, ry] - i32(0.5*candW)

      # 1. このsxyの最近傍の母点がgxyなら平均に加える
   }
}

この1の部分を埋めれば良い。

同じ母点の領域の色の平均

上記のコードの平均部分は、examplesのモザイクなどと同じ処理でいいだろう。

ということでモザイクのコードを見てみる。

let clamped = sampler<input_u8>(address=.ClampToEdge)

@bounds( (input_u8.extent(0)-1)/MOSAIC_WIDTH+1, (input_u8.extent(1)-1)/MOSAIC_WIDTH+1)
def avg |x, y|{
  rsum(0..<MOSAIC_WIDTH, 0..<MOSAIC_WIDTH) |rx, ry|{
    let [b, g, r, a] = i32(clamped( MOSAIC_WIDTH*x+rx, MOSAIC_WIDTH*y+ry ))
    [*[b, g, r]*a, a]
  }
}

アルファを掛けて足し合わせて、こうして得られた値を最後に以下のようにアルファの和で割って、アルファ自体は平均にする。

  u8[*[b2, g2, r2]/a2, a2/(MOSAIC_WIDTH*MOSAIC_WIDTH)]

a2を割る範囲は、モザイクの場合は対象範囲がすべて足し合わせる範囲なのでこれでいいが、 母点が同じピクセルの面積はもう少し細工をしないと求められない。 母点が同じ時に1を返してそれをrsumで足したものになるだろう。

let g_nn = nnEx(*sxy)
let [b, g, r, a] = i32(inputEx( *sxy ))

# sxyに対応する母点のg_nnがgxyと同じだったらこのgridColの担当範囲
ifel( all(g_nn.xy == gxy),
    [*[b, g, r]*a, a, 1],
    [0, 0, 0, 0, 0]
)

これを先程のコードに入れると以下みたいな感じか。

@bounds(GRID_WIDTH+3, GRID_HEIGHT+3)
def gridCol |x, y|{
   let gxy = [x, y] - 1
   let gs_xy0 =  gxy* GRID_INTERVAL
   let candW = 3*GRID_INTERVAL

   let [sb, sg, sr, sa, count] = rsum(0..<candW, 0..<candW) |rx, ry|{
      let sxy = gs_xy0+[rx, ry] - i32(0.5*candW)

      let g_nn = nnEx(*sxy)
      let [b, g, r, a] = i32(inputEx( *sxy ))

      ifel( all(g_nn.xy == gxy),
         [*[b, g, r]*a, a, 1],
         [0, 0, 0, 0, 0]
      )
   }

  # countは母点が同じ領域の面積  
  ifel(sa==0,
    u8[0, 0, 0, 0],
    u8[*[sb, sg, sr]/sa, sa/count] )
}

これで以下のようになった。

端も綺麗に処理されるようになった。

最後に全体のコードを貼っておく。

@title "ランダムな格子"

@param_i32 GRID_INTERVAL(SLIDER, label="Grid Size", min=10, max=256, init=150)
@param_f32 STRENGTH(SLIDER, label="Random Strength", min=0.1, max=1.0, init=1.0)

let [GRID_WIDTH, GRID_HEIGHT] = (input_u8.extent() -1)/GRID_INTERVAL + 1

@bounds(GRID_WIDTH+3, GRID_HEIGHT+3)
def gridOffset |x, y|{
  STRENGTH*[rand()-0.5, rand()-0.5]
}

@bounds(input_u8.extent(0), input_u8.extent(1))
def nn |x, y| {
  let go_xy = [x, y]/GRID_INTERVAL # x y of grid coordinate, upper left

  let nearest = reduce(init=[0, 0, 999999.0], 0..<4, 0..<4) |rx, ry, accm| {
    let gxy = go_xy + [-1, -1] + [rx, ry]
    let ggxy = gxy*GRID_INTERVAL + i32(gridOffset(*(gxy+1))*GRID_INTERVAL) # global coordinate
    let d = distance(f32([x, y]), f32(ggxy))
    ifel(d <accm.z, 
        [gxy.x, gxy.y, d],
        accm
    )
  }
  nearest
}

let inputEx = sampler<input_u8>(address=.ClampToEdge)
let nnEx = sampler<nn>(address=.ClampToEdge)

@bounds(GRID_WIDTH+3, GRID_HEIGHT+3)
def gridCol |x, y|{
   let gxy = [x, y] - 1
   let gs_xy0 =  gxy* GRID_INTERVAL
   let candW = 3*GRID_INTERVAL
   let [sb, sg, sr, sa, count] = rsum(0..<candW, 0..<candW) |rx, ry|{
      let sxy = gs_xy0+[rx, ry] - i32(0.5*candW)
      let g_nn = nnEx(*sxy)
      let [b, g, r, a] = i32(inputEx( *sxy ))
      ifel( all(g_nn.xy == gxy),
         [*[b, g, r]*a, a, 1],
         [0, 0, 0, 0, 0]
      )
   }
  
  ifel(sa==0,
    u8[0, 0, 0, 0],
    u8[*[sb, sg, sr]/sa, sa/count] )
}

def result_u8 |x, y| {
  let nearest = nn(x, y)

  gridCol(*(nearest.xy+1))
}

無事バグが治ったヽ(´ー｀)ノ

見どころの振り返り

MFGの開発の実際を伝える事は出来ていると思うが、 なかなか複雑なコードなので、全部を追うのは読んでいるだけでは厳しいとも思う。

そういう訳でこの記事の見どころなどを最後に振り返りたい。 私としては、以下の２つの点が面白さではないか、と思う。

• 複雑なフィルターを、中間テンソルの動作を確認して開発していける
• ランダムな点や母点に対応する色の計算に現れるGPU的なロジックの必要性

複雑なフィルターを、中間テンソルの動作を確認して開発していける

最終的なフィルターはかなり複雑なものとなっている。これを読んで理解するのは結構たいへんだ。 これはGPUの実用的なフィルターでは良くある事に思う（むしろシェーダーの同種のコードよりは遥かに読みやすいと思う）。

だが、これらの最終的なコードというのは、書いている側は段階的に数十行程度の短いコードを確認しては続き、 という風に進めている。

MFGは中間テンソルを自由に定義出来るため、各中間テンソルでの動作を確認していく事で、 段階的に動作を確認して、それがそのまま最終コードに転用出来る。

さらに、MFGStudioで確認はその場で画像を拡大して、バグりがちな所の挙動を目視で対話的に調べる事が出来る。

また、少し補助線などが欲しい時に、別のフィルタとして格子を書いたりする例も示せたと思う。 こうしたコードを本体からは分離したファイルに作ってそれを適用する、という事が出来るのも、 対話的に作れるMFGStudioの良い所が出ていると思う。

実際のフィルター開発の過程を、ある程度示せたブログ記事になっているのでは無いか。

ランダムな点や母点に対応する色の計算に現れるGPU的なロジックの必要性

CPUとGPUの違いは、GPUプログラムでは最初に解説されるが具体的な所がわかりにくい事にも思う。

今回のケースでは、以下の２つのケースでGPU的なロジックが出てきている。

• 格子点をランダムにずらした点を打つ所
• 同じ母点を最近傍にする範囲の色の平均

前者などは、CPUなら格子点をfor文で回して対応する位置にPutPixel的な事をすれば済む。 疑似コードで表すと以下のような感じだろう。

for(格子のx, y) {
  // 1. x, yにその格子座標に対応したランダムなオフセットを足す
  // 2. それをスクリーン座標にし、その付近にPutPixelで黒を打つ
}

この、格子の位置を元にfor文を回して、打ちたい所にPutPixelする、という考えは、CPU的な考えで、GPUでは実現出来ない。

GPUではCPUプログラムでは打たれる側のピクセルが自分で黒だよ、と言わなくてはいけない。 一番原始的に考えると以下のようなコードになる。

for(全部のピクセルのx, y) {
  for(すべての格子点) {
    // 1. 対応する格子点のランダムにずらした位置を求める
    // 2. x, yと近くにあれば黒を返す
  }
}

だがこれでは、各ピクセルですべての格子点を探索しているため、時間がかかりすぎてタイムアウトになる。 だから、この二番目のfor文を、対応しそうな格子点の候補に絞り込む必要がある。

for(全部のピクセルのx, y) {
  for(xyの近くにありそうな格子点) {
    // ....
  }
}

これはランダムの範囲から3x3の範囲に収まるだろう、とか、\(-1.5 \times gridInterval\) に収まるだろう、とか、問題ごとに考えてやる必要がある。 これは問題によっては決められない事もあり、それがGPUでプログラム出来るアルゴリズムか出来ないアルゴリズムかを分ける所でもある。

こうした話は解説を読んでも良く分からない所だと思うが、実際に格子点からランダムにずらした点を打つコードを書いてみると良くわかる。 そうした事を数十行のコードですぐに試す事が出来るMFGStudioは、 やってみないと良く分からないGPUプログラムというものを学ぶのに向いているんじゃないか。