読書記録: Understanding and Using Linear Programming
最適輸送問題の本を読むと、いつもdualのあたりで挫折するので線形計画法を真面目に勉強する事にした。 この本は短くてKindleの評判も良いのでやってみる事にする。
2章は具体例。一見LPっぽく無い問題をちょっとした工夫でLPにする。 簡単でありながら自明じゃなくてなかなか面白い。
3章 Integer Programming
解に整数の制約を入れた物を扱う章。 ちょっとした話かと思ったが、意外と重要な章っぽい。
実数に拡張した問題との対応やマッチング問題を議論したりする。 この辺は最適輸送問題の基礎となる話だね。
LPに拡張した場合にバウンドを与えるケースやそもそも意味が無い結果しか返さない場合など、いろいろ見ていく。なかなか奥が深い事が伝わってくる。
定理 3.2.1 bipartiteのperfect matching
bipartiteのperfect matching問題では、LP relaxationしたfeasibleな解が存在すれば、その中に必ず整数の解が存在している。
なかなか凄い定理だな。 最初は任意の整数プログラムの問題でそうに読めて、そんなはずないだろ?と思ったが、bipartiteのperfect matchingの場合、という話っぽい。
4章 Theory of LP, 1st steps
2章、3章は使う側の視点の話だった。 4章からLP自体の理論的な話に入る。
前提とするLPの形式
LPのAとしては以下のような形を仮定。
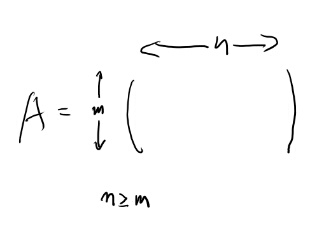
\(\bm{x}\)は\(x_1, x_2, \ldots, x_n\)。 さらに、線形独立で無い行は取り除いてあって、Aの行は線形独立とする。 そして解が少なくとも1つあるとする。
また、適当な列のインデックスのサブセットBを用いて、Aの部分行列\(A_B\) を定義する。 必ず正方行列になるように、Bはm要素。
例を以下に描いておく。
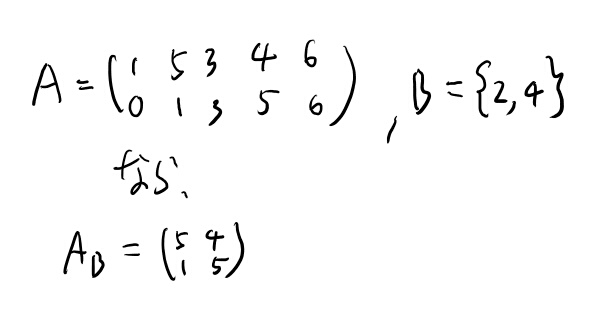
4.2 Basic feasible solution
いろいろな定義が出てくる節なので、メモを取っていく。
まずbasic feasible solutionの定義。以下のようにLPが定義されてるとする。
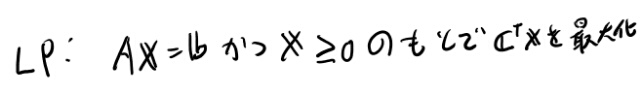
このLPのbasic feasible solutionとは、feasibie solutionのうち、以下のようなm要素のBが存在して、
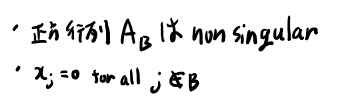
この時、\(j \in B\) な \(x_j\)をbasic variableと呼ぶ。 それ以外の変数をnon basic variableと呼ぶ。
次にbasis(基底)の定義。\(A_B\)が非特異なBの事。 Bを基底と呼ぶ事に注意。
そしてBが定める解が非負の制約を満たす時、このBをfeasible basisと呼ぶ。
basicの意味を考える
先に進んでいまいち分からなくなったので、ここで立ち止まってbasicの意味を考える。
まず、mよりも多くノンゼロのxがあったら、basic solutionが存在しない。
この状況をちゃんと理解するべく、4章の最初の具体例を考えよう。 以下のAとbに対して考える。
\[x_1+x_2+x_3 =1\]この場合nは3でmは1。 xはいろいろな値を取りうるな。 この時点ではcは出てこない。
いろいろなfeasibie solutionの中で、ゼロな変数を増やすという事を考えてみる。 大きく足し算と引き算の場合を考えてみればいいか?
足し算の場合:
\[x_i+x_j=1\]この場合、片方を大きくしていけば、どこかでもう片方はゼロになるだろう。
引き算の場合:
\[x_i-x_j=1\]この形の場合、2つの変数を共に大きくしていく事は出来る。
だが、片方を減らしていくともう片方はやがてゼロになるだろう。
feasible solutionに十分なゼロが無いのはむしろ普通な事だが、その解の中でゼロが十分あるのを探していく、という話か。 変数はxなのだな。
feasibleな解の中で0はどこまで増やせるか?は問題に依るか? Aのランクがmなので、基底はm次元に出来そうだからn-m個はゼロに出来そうな気がするな。
補題 4.2.1 Kの次元がmより低い時
補題4.2.1を考えてみる。 basicの定義のBでは、Bでない次元の変数は0な事を要求しているが、逆、つまりBの中のjで\(x_j =0\)は禁止していない。
そこでそれらの変数がある場合には、ノンゼロな軸だけ集めた時にm未満に出来る事がある。それが補題4.2.1で扱ってる場合か。
Kのrankだけ軸を取ったら、さらにm本まで列を増やしても、対応する変数は全部ゼロだからfeasibleなままのはず。さらにm本の基底が取れるはずだからBが作れるはず、という事か。
4.3と4.4 Convexity周りの定義
この辺の定義はわからなくなるので必要ならちゃんとノートとって練習問題もやっていくのだが、この本では4.3と4.4で使うだけで以後は要らない、との事。
それではサラサラ読んで雰囲気を知る程度でいいか、と思い、軽く読み飛ばす。
4.4ではbasic feasible solutionとvertexの関係とかなかなか興味深い事がいろいろ出てくるが、ちゃんと証明を追わないとしっかり理解するのは無理そうね。 そんな難しそうでも無いが、あとで出てこないならお話程度の理解でいいか、とサラサラ読み進める。ゆとり。
5章 Simplex法
LPの一つの目玉と思われるSimplex法の話に入る。 自分としては6章のdualの方が興味のある所ではあるが、Simplex法もLPをやったというからには理解しておきたい所。
5.1の具体例を実際にやる
この手のは手を動かさないと分からないので、やってみる。
最大化の対象 \(x_1+x_2\)
制約
\[-x_1+x_2 \leq 1 \\ x_1\leq 3 \\ x_2 \leq 2 \\ x_1,x_2\geq 0\]まずはこれをイコールformにする。
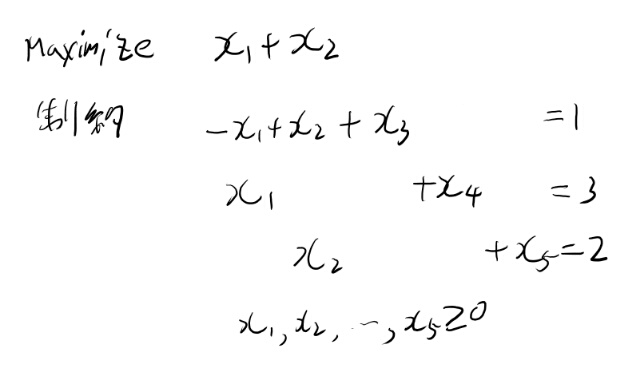
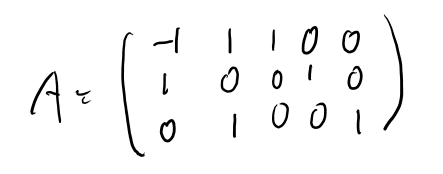
これを、Simplex表にする。
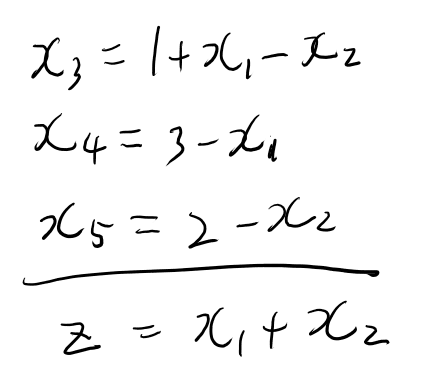
これは\(x_1, x_2=0\)となるbasic feasible solution を持つ。
ただこれ、こう簡単に分からない場合はどうなるんだろう? これはslack変数が等式の数だけあるからこう書けるのであって、最初から等式の場合はそうとは限らないはず。
とりあえず一般的な記述を読む時はその辺に注意するとして、今は先に進む。
ここから、pivotをする。zを大きくする為に\(x_1\)か\(x_2\)を大きくする。まずは\(x_1\)で。
これは2つ目の等式で3が最大か。 これで左辺を置き換えて、さらに\(x_1\)を消去する。
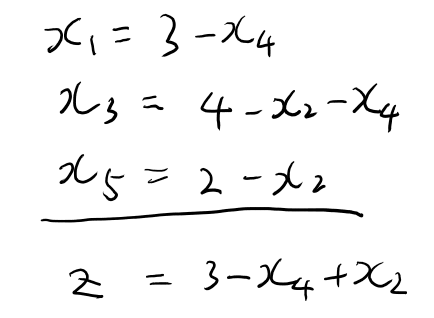
この手続きを少し考えてみる。
この手続きの前では、右辺の変数が全てゼロ、というbasic feasible solutionになっている。
この右辺の変数を一つ0じゃ無くす代わりに、新しい変数を一つ0にする。で、それだけで右辺を書くから、右辺に残る変数全てが0の解が必ずあり、これはbasic feasible solutionであり続けるな。 なるほど。
次に\(x_2\)を最大化しよう。 3つ目の式が一番強い制約で、2か。 では\(x_5\)と入れ替えよう。
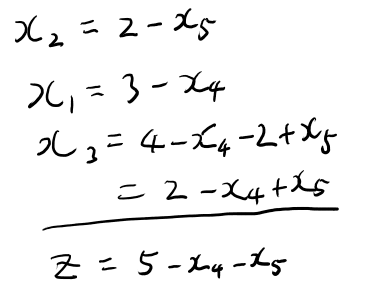
これで最大値は5という事になる。 何故かを少し考えてみる。
まずこれはbasic faasible solutionを持って、それは両方の変数が0の場合だ。 これが存在すればこれが最大なのは自明で、存在するのもbasic feasible solutionを保ったままの変形なので保証されている。
そしてこのz自体は元のzから完全に等価な変形だけで得られるので、任意のfeasible solutionで成り立つ。 よってfeasible solutionで最大の物はこれが0な物だけ、となる。
結果が最大なのはいいとして、この結果はどうして得られるのだろう?
pivotの意味を考えてみる。 zを大きくするように変数を置き換える時に、交換する変数は必ず負になる。 だが右辺に他の変数で正の物は残りうる。
有限回pivotをやった時に全部負に出来るかは分からない、というか出来ない場合はあるだろう。出来ない場合がunbound な場合のみかは良く分からないが、多分そうなっているのだろうなぁ。>そうとも限らないらしい。5.3の最後のサイクルの話参照。
Bの推移を考える。最初は3, 4, 5だった。 次に1, 3, 5になる。これは1と4を置き換えてる。 次に1, 2, 3に置き換えてる。
つまりBの軸をzを大きくするように変えている訳だな。
一般のSimplex法(5.5〜)
5.5から一般の話に進む。 説明が十分わかりやすいので、ここではメモを残す程度で。
一般のSimplex表(p65)
囲みの意味を軽く考える。
1つ目の式の形で表せる理由はなんだろうか? これは次ページのLemma 5.5.1の証明を見ながら考える方が良さそう。
\[A_B\bm{x}_B+A_N \bm{x}_N =\bm{b}\]を移行して、\(A_B^{-1}\)を掛ければ出る。 何かの定数でこう表せるのなら、zの右辺に代入することで\(\bm{x}_N\)だけの式に出来る。
ここで大切なのは、この式は単に恒等変換でたどり着ける、xの値に寄らない式という事。 だから任意の解xでこの式は成り立つ。 basic feasible solutionじゃなくてもfeasibleでさえあれば成り立つ。
次にこの解の最適条件、\(\bm{r} \leq 0\)の時について考える(p67)。 これが満たされていれば、zの式から\(z_0\)が最大なのは明らか。 というのはfeasible solutionなら\(z=z_0+\bm{r}^T\bm{x}_N\)が成り立ち、\(\bm{r}^T\bm{x}_N\)が負かゼロなので。
pivot関連の式のメモ
式5.3のあたりがぱっと見分からなかったのでメモ。
前ページのシグマで、右辺はenterしてくる以外は全部ゼロなのでシグマが消える。 enterしてくる係数だけが残る。
そして左辺はこれまではゼロじゃなかったが、このpivotでゼロになる。 すると\(x_l\)が5.3式の中括弧の形になる。 このうち一番小さい奴、というのが最初にboundされる制約という事になる。
追記: 分かりにくいのでちゃんと計算しておこう。
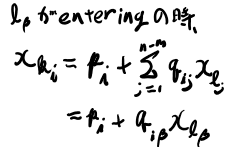
ここで、どれか一つの\(k_i\)がleaveする、つまり0になる。 これがnon negativeという条件で一番厳しくboundするものだけがleave出来る。 イコール0とおいて解くと、
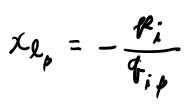
これが正のもののうち、一番小さいものがleave出来る。これが5.3式の表す事。
定理5.8.1 Bland’s pivot ruleはサイクルを生まない
そんなに重要そうにも思えない定理だが、重要だ、と書いてあるので見てみる。
記号がいろいろ出てくるので簡単にメモ。smplex表のパラメータは、
\[\bm{x}_B=\bm{p}+ Q\bm{x}_N \\ z=z_0+\bm{r}^T\bm{x}_N\]fickleな中で一番大きいインデックスvの前後を考えて矛盾を導く。
\(x_v\)がenterしてくるという事は、候補の中でvが一番小さい必要がある。 という事はvより小さいfickleのインデックスは全てこの時、zの係数は負かゼロという事になる。
この辺の事情をもとに、この時点の最適解と一致するような補助的な線形計画法の問題を考えて、これがunboundな事を証明する、というのがあらすじ。
unboundな所の条件がなぜ成り立つのかはあまりちゃんと理解出来てないが、そんな不思議でも無いのでまぁいいか。
Simplex法読み終わり
基本的な手法はちゃんと理解出来た。 多分実装もやれば出来そう。
背後にある深いトピックは雰囲気だけ感じ取ったくらいだが、この本はまさにそれを意図していると思うのでそれで良いと思う。
この本はとても良く書けているな。 非専門の人間が線形計画法を学ぶ時に必要な事が、非常にコンパクトかつ明解に書かれている。 先に進むと何があるのかがちょっと分かるのも良い。 これで自分の知らない事に出会った時の距離感というかどういう事をやらないと理解出来ないのかのあたりがつく。
6章 duality
dualityをちゃんと証明まで含めて理解する、というのは線形計画法を学ぶメインのモチベーションだったので、6章は楽しみ。
dualityの例
6.1が大変よく書けているが、先に進むと忘れがちなのでメモを書いておく。
最大化 \(2x_1+3x_2\)
制約
\[4x_1+8x_2 \leq 12 \\ 2x_1+x_2\leq 3 \\ 3x_1+2x_2\leq 4 \\ x_1, x_2 \geq 0\]という問題があった時、制約を足し引きする事で目的の式を上から抑える、という事を考える。
\(x_1\)の係数に着目すると、上から抑える条件は、非負のyを各式に掛けて足す事を思うと、以下の式が成立する。
\[4y_1+2y_2 +3y_3 \geq 2\]同様に、
\[8y_1+y_2+ 2y_3 \geq 3\]さらに、元の目的関数を上から抑える式は、制約にyを掛けて足し合わせると、
\[2x_1+3 x_2 \leq 12y_1+3y_2+4y_3\]この右辺を、制約を満たしつつなるべく小さくする、と考えると、この右辺がminimizeの目的関数となる。 これがdualな問題となる。
一般的なdualの形式
上記の例を眺めつつ、一般形を考える。 元の問題は、以下の形。
最大化 \(\bm{c}^T\times \bm{x}\)
制約 \(A\bm{x} \leq \bm{b} \\ \bm{x}\geq 0\)
dualな制約の係数はどこから出てきたかといえば、元のAだ。 不等式の右辺はc。 つまり、
\[A^T \bm{y} \geq \bm{c}\]これは元のobjectiveを、元の不等式の線形和で上から抑え込む事を考えた時に、不等式の左辺(の線形和)の各係数がobjectiveの各係数より大きい、という条件になっている。
最小化の目的関数は元の制約の右辺にyを掛けたもの、つまり以下になっている。
\[\bm{b}^T \bm{y}\]これが式D。 これは元の不等式の線形和の右辺で、これで上から抑え込めている。
この抑え込めている上限をなるべく小さくしていく、というのがdualの問題設定となる。
6.1.1 weak duality theorem
ちょこちょこ使うのでメモしておく。
dualの問題設定で、PとDの両方のfeasibleな解、xとyを考えると、以下の不等式が成り立つ。(yの式でバウンドされる)。
\[\bm{c}^T\bm{x}\leq\bm{b}^T\bm{y}\]もともとdualというのは、不等式制約の線形和でobjective functionを上から抑える、という話だったので、それを思うとこれは自明と言える。
より具体的には以下。
\[\bm{c}^T\bm{x}\leq \bm{y}^T A\bm{x} \leq \bm{y}^T \bm{b}\]Farkasのlemma
dualityを理解するにはこちらからの証明の方が良さそう。 という事でfarkasのlemma周辺のノートを簡単に作る。
6.4.1 Farkasのlemma
Aがm行n列の実行列とする。 そして\(\bm{b}\in\mathbb{R} ^m\)とする。
この場合、以下の2つのどちらかが必ず成り立つ
- \(\bm{x}\in\mathbb{R} ^n\) で \(A\bm{x}=\bm{b}\) かつ \(\bm{x}\geq 0\) なるものが存在する
- \(\bm{y} \in \mathbb{R} ^m\) で \(\bm{y}^TA\geq \bm{0}^T\) かつ \(\bm{y}^T\bm{b}<0\) なるものが存在する
6.4.2の幾何学的解釈がなかなか良い。 証明もだいたいこれに沿ってるので、これだけ理解しておけば雰囲気的には十分。
aの非負の係数の線形和でbが表せるか、表せないならコーンとbを分離する平面がある、という事。
6.4.3 Farkasのlemmaの3つの表現
- \(A\bm{x}=\bm{b}\) が非負の解を持つのは任意の\(\bm{y} \in \mathbb{R} ^m\) で \(\bm{y}^TA\geq \bm{0}^T\) ならば \(\bm{y}^T\bm{b}\geq0\) となる時だけ
- \(A\bm{x} \leq \bm{b}\) が非負の解を持つのは任意の非負の\(\bm{y} \in \mathbb{R} ^m\) で \(\bm{y}^TA\geq \bm{0}^T\) ならば \(\bm{y}^T\bm{b}\geq0\) となる時だけ
- \(A\bm{x} \leq \bm{b}\) が解を持つのは任意の非負の\(\bm{y} \in \mathbb{R} ^m\) で \(\bm{y}^TA= \bm{0}^T\) ならば \(\bm{y}^T\bm{b}\geq0\) となる時だけ
このうち2を使う。 1から2は、1を所与とすると2を変形して1に出来る、という事を使う。 これはm個の変数を足すというこれまでやってた話と同じ。
全体の感想
6章はまぁまぁ真面目に最後まで追った。 7章はざっと読んで、その先は読んでないが、6章まででいいかな、と思ったのでここでこの本は終わりとしておこう。
で、感想。とても良い本で感動した。
まず短い。短いからやる気が出る。
そして具体例や高校生レベルの初歩的な計算くらいでの話がかなり多い。 そのおかげで、難しい部分を追わなくてもほとんどの議論が理解出来る。 また難しい議論を追う時も具体例がとても助けになって追いやすい。
また、証明などを最短のルートでせずに、まず、簡単に分かる所と天下り的にlemmaを与える事を組み合わせて、 lemmaを飲み込めば簡単に理解出来る、という形を示す。 しかもlemmaの具体例とか直感的な理解とかも豊富に解説する。
で、そのあとにそのlemmaのちゃんとした説明をやる、というパターンが多い。 lemmaを感覚的に理解して証明の大筋を理解すればだいたいは事足りるし、ここまではかなり簡単に到達出来るように工夫されている。
この証明の途中で挫折する人にもなるべく多くを伝えたい、という姿勢が数学の本にしてはすごく珍しいと思った。 具体例とか、こうした遠回りとかが多いので、最短で簡潔に書かれている訳では無い。 むしろこんな冗長に書いてある数学書も珍しい。それでも全体としては短い、というのが本書が良く書けてると思う所だ。 トピックの取捨選択がすごく上手いのだろう。
また、線形計画法というもの自体がなかなか面白い。 問題設定は基礎的な線形代数の、実数行列とかでそんな難しさは無い。 ただ線形代数的な理解、例えば行列の各行や列をベクトルとみて線形和を取ったりする時の、元の行列の性質との関係とかが割とたくさん出できて、まるで線形代数の例題みたいにいろんな性質を使う。 この線形代数の強力さがいろいろな所で見れる所にまず面白さがある。
さらに、線形代数的な知識で話題が理解出来るのだが、その先の豊富な数学につながっているのも分かる所が面白い。
特に幾何学などは大学レベルで良く出てくるconvex polyhedraなどがバリバリ出てきて、高校生の入門的な簡単な式からどんどん数学の深い所につながっていく感じが、分野としてとても興味深いと思った。
大学一年生が線形代数を学び終えたあとに、先に進んでしまわずに一度こういう分野を学ぶと、数学の意義とかさらに学ぶ意欲とかが高まって良いよなぁ、と思った。
そしてそういった事を理解出来るように書かれている、というのはこの本の良い所と思う。 じぶんはこの本を読むまで、線形計画法とは大学受験の簡単な奴で出てくる程度の問題しか知らず、なんでこんな分野に独立した教科書が存在しているのか分からないレベルだったが、今はかなりこの分野の広がりというか、全体図の概要みたいなのは理解出来たと思う。
この本を読む人が期待するのはまさに線形計画法というのは何なのかという所だと思うので、そういう目的にはとてもオススメの本だと思う。 しかもちゃんと数学の教科書として書かれているので、読み終わったあとにちゃんとした教科書を読まないといけない、という感じでも無い。
線形計画法に興味がある人にはとてもオススメ出来る決定版のような教科書だ。私は大絶賛。