サイコロ本(Foundations of Statistical Natural Language Processing)、1章から10章まで
BERTがなかなか良さそうなので、次はNLPやろうかな、と思い、サイコロ本を読んでおこう、となる。
自分の認識だとこの本は定番の教科書だがニューラルネット以前の奴という位置づけ。 まぁembeddingsとかencoder-decoderとかは知ってるので、むしろこういう奴の方が自分には必要かな、と思い読む事に。
自分の前提知識
自分がこれまで読んだ本。
昔機械翻訳の研究をやろうか、と思った事があって、研究室を選ぶ為に教科書を学ぼう、と思った事があった。 seq2seqとかより前の頃。 で、この教科書読んでたら、自分がドクター取る頃にはこの問題片付いてそうだな、と思ってやめた。
トピックモデルが知りたくてこの本読んだ事がある。一応ちゃんと理解した(もう忘れたが)
ちゃんとRNN使った自然言語処理を理解したいと思って読んだ。結講真面目に読んだ気がする。
その他seq2seqとその周辺の論文とか、word2vecとかは一応読んで、だいたい理解してたと思う(もう忘れたが)
またグラフィカルモデルは結講真面目に勉強してて、HMMとかは実装も数学的な話は証明とかも割と真面目にやってて結講得意。
という事で何も知らないという訳でも無いがちゃんと勉強した、という訳でも無い状態なので、基礎をちゃんと勉強してみよう、と思った次第。
ただこの辺の式追うのはそんなに困ってないので、式変形とかを頑張って追うかは未定。読んでから考えます。
Road map
全4部構成で、Part1は数学とかlinguisticとかの入門らしい。さすがに飛ばし読みでいいか?
Part2はWord。 ここが一番真面目に読みたい所かな? collocation、disambiguation、attachment disambiguitiesとかが大切らしい。たぶん知らなさそう。
Part3が文法。 最近あんま見ない話題ね。
Part4が応用。 IRとかテキストのカテゴライズとかの話らしいので、意外と興味深いかも。
1章 イントロダクション
序盤の真の文法みたいなルールでは無くただ存在するテキストを確率的に扱うjustificationの所が難しい。 前置詞がどうとかの文法用語にあまり慣れてない上に英語のきわどい使い方についての話が多いので、自分の英語力では判断出来なかったり何を言いたいのか分からなかったりする。
英語力不足は仕方ないのでこの辺は読み飛ばすかなぁ。 そして現代機械学習屋としては、empiricismへの批判というのが良く理解出来ない。 確率モデルは簡単な事しか扱えないと誤解されがちとか言われても、そんな誤解してる奴はもはや居ないのでは…
なお、Corpusはテキストのbodyの事だ、と書いてある。bodyというのは本文という意味かね。 なんとなく語彙の辞書みたいな意味と思ってたが全然違った。
パースの方法とか単語のdisambiguationがどうとか言ってるが、最近のBERTは割とWittgenstein的な単語の意味とか文脈をそのまま学習してて、こういう要素は無い気がする。
こういう一つ一つを正しくやるのが極めて難しい物を積み重ねるって、いかにもあんまうまく行かなさそうだよな。
一回しか出ない単語をhapax legomenaって言うらしい。ギリシャ語。何故。
一回しか出ない単語が多い、という話。 この前見た論文はトリグラムのベクトルで単語を表してたな。bertはこの問題にどうアプローチしてるのかしら?
Zipf’s law
おお、ようやくなんか知ってた方が良さそうな話になってきた。 そうそう、こういう背景知識みたいなの知りたくてこの本読み始めたのだよね。
こういう既知の、言語に関する洞察は知っておくと良い事ありそうたよな。 この周辺の話は面白い。
1章を読み終わって
まず最初の印象として、英語の文法の知識が足りないな、という物。 文法用語も知らないし、英語のややこしい用法とかも分からない。 言葉的な事で勝負するならちゃんと英語の文法書とかは勉強した方が良いな、とは思った。 一章が特別そういう記述が多い、というのを期待したいが。
また、現代に役に立たなくなった事も多そうだな、という所。 これから学ぶという時に要らない物を判断する、というのは難しさもあるが、 要らなさそうな所で面倒な所は適度にサボって進めたい。将来何が役に立つかは分からない、という部分はあるが、費用対効果はやはり考えたい。
ただ現代でも役に立つ事も多く載っているな、とも思った。
2章 数学
確率論とかの話。シグマ集合体とかがinformalに導入されて、へーとは思ったが、さすがに知らない事は無いかなぁ。
Example2を解いてみる
簡単なベイズ統計の入門の話題だが、 たまにはやらないとカンが鈍るのでやってみる。 テストが陽性なのをテ、parasitic gapがある事をパと書く。
なお、parasitic gapがなんなのかは知らない。
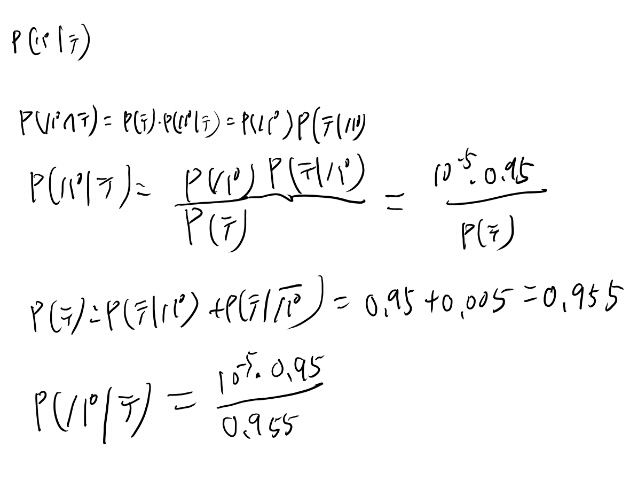
うむ、さすがにこの位は解けるな。よしよし。
エントロピー Example9
いい練習という事でエントロピーの計算をやっておこう。
まずH(C)を出す。
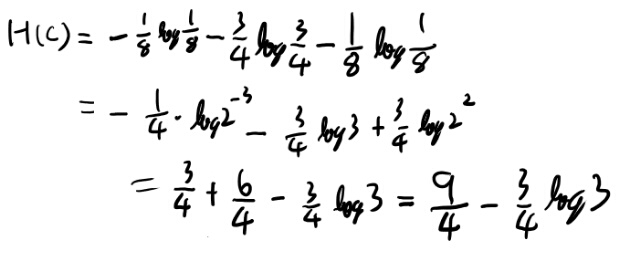
ふむ、問題無いな。次にV given Cのエントロピーを出そう。
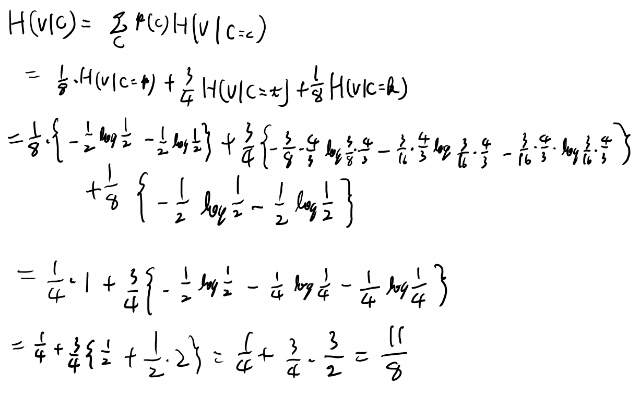
各場合で1に規格化しないと駄目なのね。
次に本では、H(C, V)を積の法則に相当する式で出している。 まずはこの式を自分でも証明しておこう。
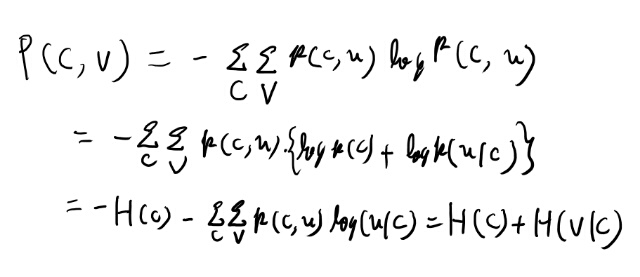
最後の等号は定義のような物だが、いまいちピンとこないので少し考えておく。
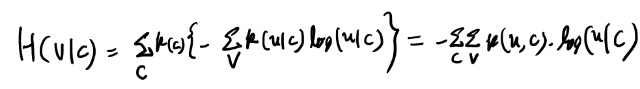
真ん中の式は中括弧内の期待値になってる。 各Cの値での条件付きエントロピーの期待値になってる訳だ。なるほど。
積の法則に対応するchain ruleは、ようするにCを送ってからCの値を使ったエンコードでVを送る時の平均ビット数、と考えると納得は出来るな。
さて、同時エントロピーはせっかくなので本とは別の方法で導出してみるか。 定義に従い、同時確率で出してみる。
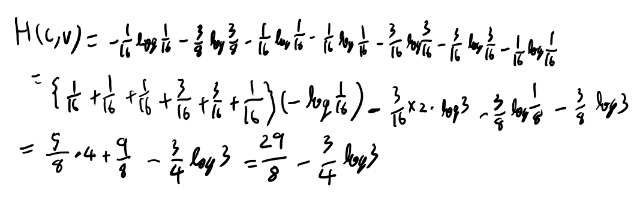
うむ、特に問題無いな。
Entropy rate
唐突にサブスクリプトでサブシーケンス表すノーテーションと同時に導入されるので分かりにくいが、単語がn個来る時の、n単語の同時エントロピーをnで割った物か。
同時エントロピーのランダム変数をどんどん増やすとどんな感じかイメージするのは難しいが、何かその極限が表す概念に意味がある事があるのだな。 これは先に出てくるのだろう。
2.2.3 Mutual information
初めて見る気がする話だな。ただなんか見覚えはあるので昔どっかでやったのかもしれない。 何にせよ覚えてはいないな。
情報理論っていまだにちゃんとやった事無いんだよな。 そろそろやっても良い頃な気はする。
この本でもCover and Thomasが薦められてるな。Goodfellow本でもこの本が薦められてたのでこれ読むかなぁ。
2.2.4 noisy channelと翻訳
おぉ、Encoder-decoderモデルっぽい! 本来はこういう背景を元にRNNで実装したのがEncoder-decoderモデルなんだろうけど。
逆にこういう定式化の汎用性の高さは、汎用noisy channelモデルが出来たらこれだけの応用がある、という事だよな。 それは数年以来に来そうな未来だやね。 楽しみだ。
2.2.6 cross entropyの話(が分からない)
式2.48がいまいち分からない。H(L, m)という奴。Lがなんなのか分かってないな。
まず定義式を真面目に見よう。
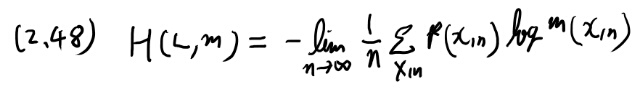
良く分からないので、limitを取る前の適当なnについて考えてみよう。
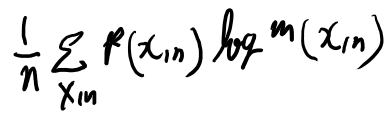
和は何について取ってるか?というと、X1, X2, … , Xn までのランダム変数のシーケンスだよな。
ややこしいが、各ランダム変数は単語を表す実数値なのだろう。 ようするにこれで単語がn個連なった文を表す訳だな。
pの中もmの中も同時分布を表しているのだろう。 だから前後関係とかは関係ある。
シグマの中を考えてみよう。 pはそんな単語列の文が現れる確率だな。 これはたぶん長さnの文、というのを母集団としててその中で規格化されてるのだろう。
logの中もpだったらこれは単なるエントロピーだな。 それを言語モデルmに置き換えてるのだから、ようするにpとmのクロスエントロピーか。
あー、文とは限らないか。むしろ文と文をつなげて、そういう文が連続すればOKなんだな。とにかくどこまでも続く単語の列を見ていく訳か。
凄く大きなNという数字でこれを考えると、なんかずーっと続く文をN単語目まで見る、をいろんな文書などで繰り返す訳だ。 で、それらの単語の列がそれぞれ現れる可能性をpとして、言語モデルでその単語の列が現れる可能性をmとしてそのクロスエントロピーを出すのだな。
さて、次の2.49は、niceな性質なら成立する、と言ってるがniceってなんやねん。
とりあえず式の意味を考えると、十分に長い一文の同時確率と、十分に長い単語列をいろいろ集めた時の同時確率の期待値が一致する、と言っている。 つまり十分に大きな数Nを固定して、このN個の単語列をたくさん集めると、どの単語列の出てくる確率も一緒と言ってるんだな。
それが何を意味するのかは分からないが、そんな不自然な事でも無い気はする。
追記: あとでこのniceな性質に言及があって、Shanon-McMillan-Breimanの定理と言うらしい。
2.2.8 Perplexity
分からない記述があるのでメモを残しておく。 2.53の右辺は以下のように、Hの中は小文字になってる。

こんなのの定義はあったっけ?と前を見直したが見つけられなかった(探し方が不十分かもしれない)。
確率変数に対しての定義は、式2.46にある。 書いておくと、確率分布pに従う確率変数Xと、pとは別のpmfであるqに対して、Xとqのクロスエントロピーとは以下の式で定義される。
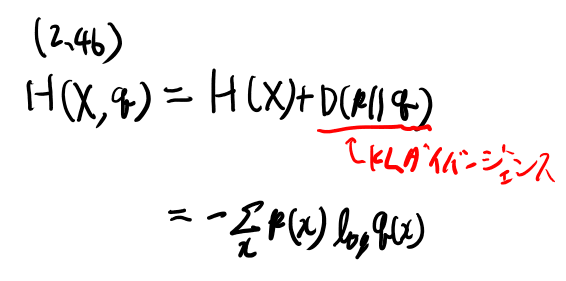
これは普通のクロスエントロピーの式だが、Xとqで表記されてるので注意が必要。
さて、式2.53の右辺はこのポイントワイズ版に見える。 2.54式から逆算して考えると定義は以下か。
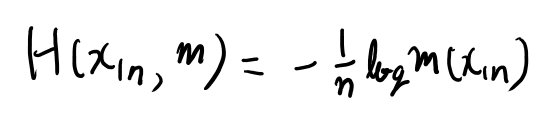
あ、式2.50の右辺だな。この式にこういうノーテーションを与えたのかな。 これは式2.50によればLとmのクロスエントロピーの近似値だ。
つまり2.53はLとmのクロスエントロピーの近似値とperplexityの関係か。
perplexityがkの時は、基本的に各単語を、毎回「次はこのk通りのうちのどれかだな」と思って見てる事に相当するらしい。
2.54の右辺をk乗して、積の法則で一文字ずつ見ていく時の条件付き確率の積とすればそうなってるな。
2章読み終わり。勉強になった!
最初は読む意味無いかな、と思ってたが、Information theory周辺はとても勉強になった。Information theoryやらんとのぅ。
perplexityとか良く評価の所で出てくるが分かってなかったので、今回ちゃんと理解出来て良かった。
2018年現在でも、なかなかこの本は読む価値があるな。続きも楽しみ。
3章 Linguistic Essentials
英語の文法の専門的な話で、予想以上に辛い。 話題にしている内容が英語の特殊な用法とかだったりするので、そもそも知らなかったり、知っててもあまり詳しくはない場合もある。
文法用語も知らないのが多く、非ネイティブは不利な分野だなぁ、とか思う。
ただ意外と義務教育でやった英語はこういう話が多く、全く歯が立たない訳でも無い。 英語の文法の参考書とかって向こうの文法書とかを参考に作られてたんだね。当たり前か。
英語の勉強と前向きにとらえて頑張って読む。
3.1 品詞とか
Parts of speechと言うらしい。 名詞とか形容詞とか動詞とかをいろいろ説明し、Brown tagでは何が割り当てられているか、を説明している。 細かい分類は良く理解出来ているとは言い難いが、どんなタグが割り振られているかの雰囲気はつかめた。 大変辛かった。
3.2 文の構造的な話
文法の木のあたりで略語が良く分からなくなってきたのでメモ。
NPはnoun phrase、VPはverb phrase、PPはprepositional phrases、APはAdjective phrase(形容詞句か)。
さらに前節のBrown tagが混ざってるのか。Table 4.5に一覧があるのでこれを見ながら頑張るのね。
文法用語に慣れてきたせいか受験英語程度の文法知識で対応出来るからか、とにかく3.2の方が読めるな。 文法用語の勉強として読むか、と自分の中にモチベーションが作れたせいかもしれない。
ドメインの知識について
SVMくらいまでの機械学習というのは、ドメインの知識をモデルに入れ込むのが重要だった気がする。 サイコロ本の三章などもそういう事の基礎に思う。
一方でXGBoost以降だと、ドメインの知識を学習出来るように問題設定を考える方がよくなったよなぁ。
BERTやencoder-decoderなど、ドメインの知識はあまりモデルの構造には入ってないし、 そちらの方が筋が良い、と我らも感覚的に感じる。
なんかそこには時代の違いがある気がするね。名前つけても良さそうだが。
4章 Corpusとかプログラムとか
3章の辛さが嘘のようにスラスラ読めるな。 エディタはemacsがいいぜ、とか、正規表現便利だぜ、とか、Cは速くていいがPerlも前処理とかには楽だぜ、とか、話題が突然知ってる話になるからだな。
4.2 トークナイズの話とかは辛い
コンピュータに扱うのが難しいケースは非母国語話者にも難しいな…と思う例が多い。 難しい英文をたくさん読むので大変疲れる。 しかも幾つかは分からなかったりもする。
NLPの話では無いと思うがこういうのはサイコロ本辛いよなぁ。
5章 コロケーション
英語の例文の難易度は相変わらず高くて辛いが、コロケーションという現象とそれをどう扱うかという話自体はそんなに英語の文法知識は要らないので、3章や4章よりは大分楽に読める。
5.3.1 t検定
おぉ、コロケーションの判定の為に、t分布で検定とかしてる。 なんかこういう昔ながらの統計の話って最近まったく見ないよねぇ。 練習として解いてみても良いかと思ったが、必要な数がどんどんあとから出てくるからやめ。
基本的なアイデアとしては、
- 単語の頻度からそれぞれの単語の出る確率を出し、積を同時確率とする
- new companiesの出現をバイグラム群からのこの確率によるベルヌーイ試行とみなして平均、分散を計算
- 実際の登場確率をサンプル誤差としてt検定を行う
という感じ。
なお、そのあとにstop wordを消すとだいたい有意になる、みたいな話が書いてある。 単語はランダムじゃないからだ、みたいな事言ってる。 で、検定で有意かどうかじゃなくてランキングとして使え、と書いてあって、それの統計的意味付けとは…とかいう気分になる。
これなら普通に事後確率をスコアとする方がクリアだよなぁ。
5.3.3 ピアソンのカイ二乗検定
なんか懐かしい物が続くな。 いい機会なので昔勉強した統計の入門書の該当箇所を読み直すなどする。 統計は自炊するようになったあとに本格的に勉強しはじめたので、この辺もギリギリ電子化されてるのだった。
と思ったが式5.7は無いな。導出するか。
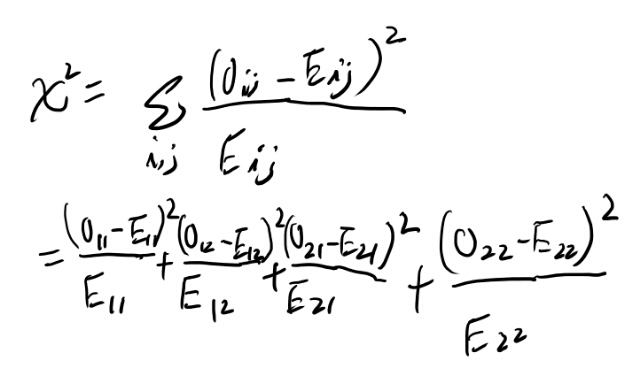
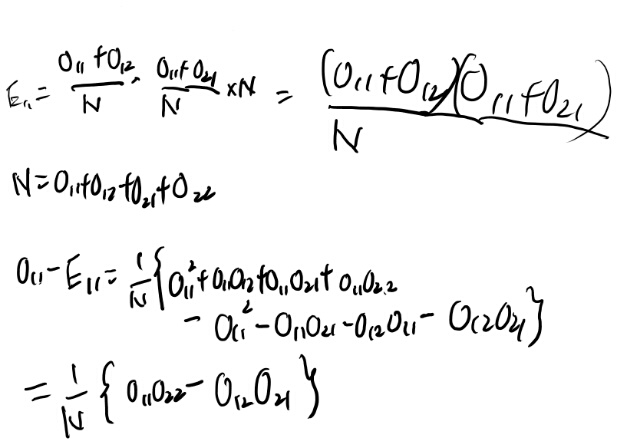
う、これはなりそうな気がするが、めんどくさいな。 まぁ頑張るか。
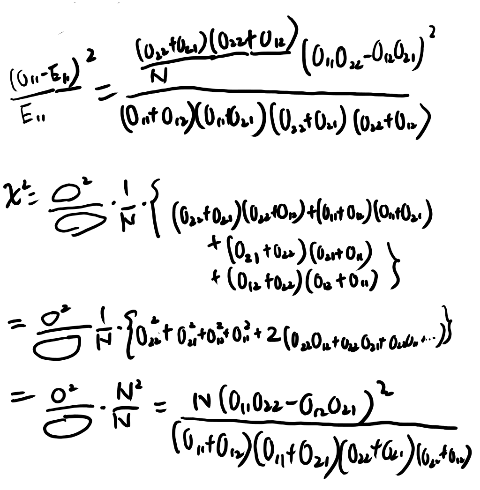
頑張った。なりそうね。 なんか昔証明したことあるな、これ。
tfのカイ二乗スコアで類似度を測る
こんなやり方あるのね。知らなんだ。 ただこれだけだとその言語の比率を表してる場合もあるので、一般的な比率とも比較しないといまいちな気がするが。
なんにせよ、corpusの類似度は現代でも興味深い問題ではある。
5.3.4 Likelihood ratios
Likelihoodは慣れたもんだが、Lがなんなのか分かりにくいね。 これはそれぞれの前提で、w2がc2回観測される尤度なんだな。
L(H1)は、
- 「c1個のw1から、c12が得られる尤度」
- 「N-c1個のそれ以外の単語からc2-c12が得られる尤度」
で、その積でw2がc2個得られる尤度を求めてる訳だ。 L(H2)も同様。 pやp1, p2から二項分布を仮定して尤度出す所と、このLがなんなのか、というところで二箇所難しい場所があるので、この解説読んでさくっと理解するのはなかなか難度高いな。
c1は所与というか、その尤度は考えてない。当然2つの仮説で同じだから正しいのだけど、ちょっと説明無いのは不親切ね。
5.4 Mutual information
5.11でpoint wiseなmutual informationの定義が出てくるのだが、そんな値が何に使えるんだ?というのが良く分からない。
で、先を読んでくと、やはりいまいちでその理由が書いてあるが、そもそもこの値を何を期待して使ってたのかの方が良く分からない。
結論としても、uncertaintyのreductionの度合いは別に興味深いコロケーションを示唆する訳じゃない、と言ってて、定義からそりゃ明らかだろう、という気もしてしまう。 わざわざそんな事に言及するのは、なんかこういうのが誤って良く使われてた時期があるのかね?
5章読み終わり
この辺から英語の文法のお勉強感は減ってくるね。 コロケーションはskip-gramとかと近い話なので割と馴染みはある。
やけに検定にこだわる所が最近の本とは違うなぁ、と思うが、結果を単にスコアとしてソートするなら検定の枠組みにこだわる必要は無いのでは… 別にカイ二乗のスコアが高い方が関連が深いことを意味する訳じゃ無いのだし。
そういう訳で解法はどれもあまり凄いアイデアとは感じなかったが、問題を理解しておくのは現代でも有意義と思うので、読む価値はあった気がする。
ついでに検定の復習にはなった。最近検定とかやらんからね。
6章 言語モデル
n-gramで言語モデル作ってみる、という話。 この辺は自分でも同じ事やった事はあるし別に難しい事は無い。
6.2 n-gramの言語モデルいろいろ
出てこなかっかバイグラムが多すぎてナイーブに扱うと問題が出る、という話から始まり、ふんふん、と読んでいく。
なんかいろいろなモデルが出てくるが、何故か導出が無い。適当なprior置いて簡単に定式化出来そうなのに。 なんかそういうの真面目にやる本と思ってたが違った?
まぁどれも割と素朴なモデルなのでいいか、と読んでいくと、最終的にはGood Turing Estimatorがいいぜ、と言ってくる。
なるほど、と読んでいくと、スムージングしたカーブをなんかアドホックにつなげる、とあるがいまいち詳細が良く分からない。 そのあと具体例で計算してみるぜ、と続くので気合入れて読むか、と思ったら、 実際の計算はwebにあげておいたプログラムでやったぜ、とかいって解説が無い…
えー!?詳細はwebで!って奴!?そりゃ無いよ…
Good Turing Estimatorのコードを読む
6章のwebはここか。 そこからCのコードへのリンクが貼られている。
最初は入力をテキストと思ってたので意味が分からなかったが、どうも入力は、文中で言う所のrとNrを一行につきスペース区切りでひとつずつ書いた物ってぽい。 rの昇順っぽい。
あとで読み直す時の為に軽く説明を書いておくと、rはCorpus内でn-gramが何回出てくるかを表す。
例えばabが10回出てくるならrは10となる。 Nrはrがr回のn-gramの数。 つまり、N_10なら、10回出てくるn-gramが幾つあるか、という事。
readValidInputではこれらの空白区切りの数を読んでいって、配列rに何回出てくるかを、配列nに文中のNrを入れている。
rはだいたい0, 1, 2,と順番になりそうだが、理論上は5回出てくるn-gramと7回出てくるn-gramはあっても6回は無い、という事がありそう。
で、これでセットアップした配列を使ってanaylseInputを呼ぶ。 これが実際の仕事をする関数っぽい。
bigNはCorpus内の、重複もカウントしたn-gramの個数だな。 PZeroはなんだろう? 一回だけ出てくるn-gramの比率に見えるが…
row(1)という関数はrが1のインデックスを返しそう。普通に考えれば1なのでは? (データが猛烈に多い場合のバイグラムとかならrが0な物が無い場合もありえるかもしれないが)。
そう考えるとPZeroはN1/Nに見える。 N1はNrのrが1の物という意味ね。
次のfor文ではlog Zとlog rをキャッシュしていく。 log rはいいとして、Zってなんぞや?
コードが読みにくいが、端以外では、iは一つ前のr、kは一つあとのrが入っている。 つまり、
\[Z_j = \frac{2 \times N_j}{r_{j+1}-r_{j-1}}\]っぽい。(注: 今サイトのバグで数式が出てません。来週日本帰ったら直します)
分母は普通2だよな。するとzは普通はNiと一致するのか。 どういう時一致しないか?というとrが飛び飛びの時だよな。
例えばr=5で、その下が4、その上が7としよう。 するとこの分母は3となる。
N5を2/3した物という事になる。
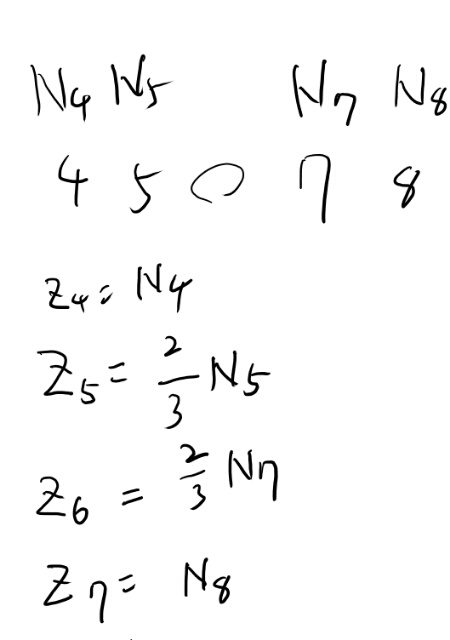
こんな感じになるが、このZはなにをしたいのだろうか。 最終的にはrからNrをもとめる回帰式を求めたいのだよな。
分からん。
findBestFitを見るとlog rとlog Zの単純な線形回帰をしているようにみえる。
抜けてる所を何かしてるように見えるが、回帰のx側はrを使ってるので、4, 5, 7, 8のままなのだよな。
5と7が少し小さくなるみたいだが何故だろう?分からん。
仕方ないのでそのまま進む。 smoothedが先程いったように線形回帰した結果。
281行目のyは教科書にもある推定値だな。
その次の283行目のif文とindiffValsSeenとはなんだろう?
rowという関数は、引数の値と同じrを持つrowのインデックスを返す。 rj+1が無いとは、この次が抜け番の場合か、最後の場合の処理だよな。
xはSrじゃなくてNrを使った場合の推計値か。 if文の条件は読みにくくて泣いちゃうな。
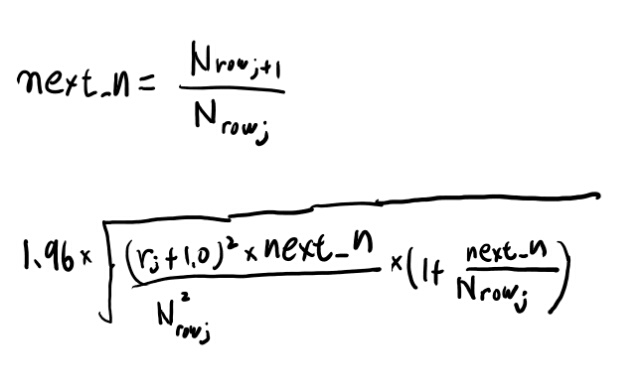
だいたいこんな感じか? この最後の式が、回帰版の推計値のyと実測値版の推計値xとの差より大きいとxを使うらしい。
この条件がどこから出てきたかは良く分からないが、本文でrが小さい時は推計値じゃなくて実測値を使え、と書いてある、その条件なのだろう。
ソースの概要を理解して、細かい所に分からない所はあるがだいたいどう実装するかは理解した。先に進もう。
追記: 6章の最後を見てたら、注12にこの式とおぼしきものが載ってた。 これは標準偏差との事。 教科書の数値は1.65となっていてコードの1.96とは違うが、まぁそこはいいだろう。
なんでこれが標準偏差になるかはちょっと考えただけでは分からなかったが、それっぽい形なので導出は頑張らないで鵜呑みにする。
6.21式のメモ
式の意味が良く分からなかったがあとの例を見て分かったので解説を書いておく。
分子は対象とするn-gramの出現回数で、分母はそのn-gramの次の単語がどれくらい多様かを表している。
of thatは178回出ているが、of thatの次の単語はバラバラで115通りある。 つまりこのバイグラムのあとに文法的にありえない、という単語はあまり無い。 この2つの数を割った178/115は1.55。
一方great dealも178回だが、その次の単語はより限られていて36種類しか無いらしい。 だからこのバイグラムのあとは文法的にありえない組み合わせが多そう。 178/36は4.94。
この1.55とか4.94に応じてグルーピングし、それぞれのグループごとに一つのラムダを割り当てて、それらの値を6.20式としてEM法で最適化する、という事だと思う。 historyをこのグルーピングの値を計算するのにだけ使う、という事か。
イマドキのスコアと比較してみよう
n-gramの洗練されたモデルにより、perplexityが240という洗練したスコアを達成した!
という事でイマドキのモデルでのスコアを冷やかしてみよう。 同じデータセットで比較しろよ、と言われそうだが旅先だしね。
で、bertはそれっぽい物を見つけられなかった(Table 6のpplは4前後っぽい気もするがテストセットでのスコアじゃないよな、これ)ので、一つ前のOpenAI GPTで。これもTarnsformer時代の相当強いモデル。
で、この人達のcorpusでは18.4だって! 一桁小さいね。 次の単語を予測する時、だいたい平均18択くらいには絞れる、という事らしい。 ほんとにそんな低いのかな?試してみたいね。
6章のn-gramモデルを読んで
バイグラムの分布をかなり正しく予測出来る、というのは分かった。 モデルはかなり原始的で、変な調整が入ってるにせよ、単純にr回出現するn-gramの数から割とストレートに予測している。
これはこれで一つの結果とは思うが、言語モデルとしては貧弱だなぁ、という印象も拭えない。 結局n-gramでは、大半は見たこと無い物になってしまうので、良くある物とユニグラムの組み合わせみたくなっちゃう。
単語の前後関係から何かを学習してくれないとねぇ。
ただ単純なモデルなので、問題を理解する為のスタート地点としては良いね。 やはり最初は簡単な問題から始めないとね。
7章 Word sense disambiguation
複数の意味のある単語のうち、どの意味かを当てる、みたいな話。 こうやってここの要素を積み上げるって2018年の感覚だといかにも上手く行かないやり方だが、教養として知っておく事には意味はありそう。
7.2.1 ナイーブベイズ
ふんふん、と読んでたらナイーブベイズが。懐かしいな。 ただどこでやったのかが少し調べたが出てこない。たぶんCourseraのPGMかな。 他でもやった気がするが…
やはりdaphneのPGM本には載ってるな。 この本はadobe DRMでビュワーが腐ってるから開くの嫌なんだよな…
今だとKindle版があるので世界は平和だね。 3.1.3.2がナイーブベイズ(p49)。
とりあえずグラフィカルモデルを書いておこう。
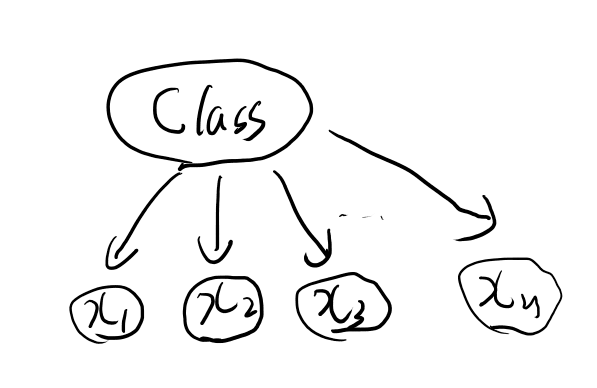
ナイーブベイズは、目的の事後確率である条件つき確率の、条件がcondititionalyにindepenentという事かね。 この時のcondititionalyはベイズルールで反転した、つまり目的とするskの事だ。
お、式3.6でそう書いてあるな。
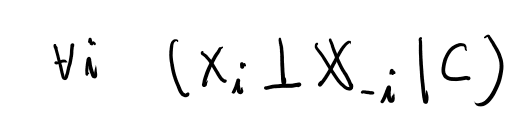
この仮定を置くと、単純な各単語の尤度の積になるのでバイグラムをカウントするだけで簡単に推計できる。
この頃のモデルは簡単でいいね…
7.2.2 Information theoretic approach
お、例のフランス語の意味が分かる! フランス語の多義語の話をしてるが、ここはフランス語知らないと分かりにくいな。ふふん、俺様教養人なのでこのくらいの単語は分かるぜ。 という事でちょっと分かりやすくて得した気分。
このmutual informationというのはあまり良く理解してないが、式の意味は確率論的にとらえてもここでのアルゴリズムは問題無さそうなので深く考えずに読む。
具体例を挙げてくれているのでこれを追ってみよう。 まず前提から。
prendreの意味を推測するタスクを解きたい。 候補はt1からtmで、この場合はtake, make, rise, speakのどれか。
で、ヒントになりうる単語はx1からxn で、この場合はmeasure, note, example,. decision, paroleのどれからしい。
paroleは知らない単語だな。 辞書を引くと「言葉、発言」などの意味で、「prendre la parole」で「発言する」という慣用句らしい。へー。知らなんだ。
なお、英語もrise to speakで立ち上がって話しかける、みたいな慣用句らしい。こちらも知らんがな。
事実をまとめると以下だな。
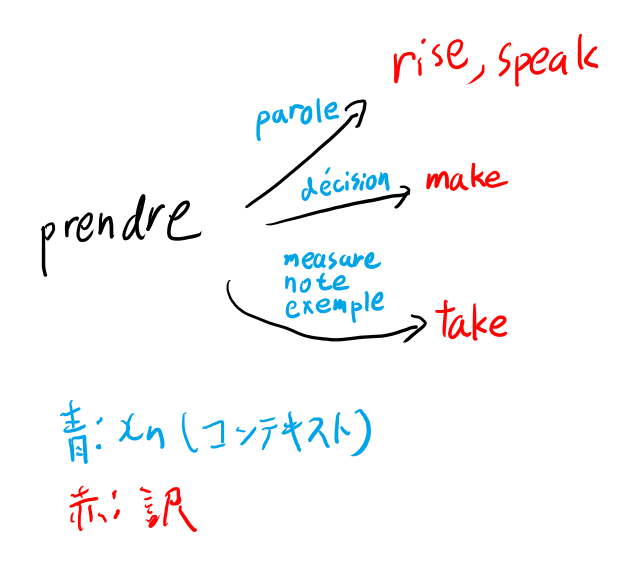
で、FlipFlopアルゴリズムはまず赤文字を2つのグループにランダムにわけて、これをP1, P2と呼ぶ。
最初は
- P1 … take, rise
- P2 … make, speak
と分ける。riseとspeakが別なのは残念だが、ランダムなのでそういう事もある。
で、次にこれとのmutual informationが最大になる青文字の分割を考える。 つまりヒントとして何があれば一番P1とP2のどちらか見分けやすいか、と考えれば感覚的にはいいかな。
riseとspeakはどうせ区別出来ないので、take とmakeだけ考えると、
- Q1 … measure, note, exemple
- Q2 … decisision
で、parole どっちでも良い。テキストではQ2に含めている。
次にこのQ1とQ2を固定としてPの方の分割を見直す訳だ。 これはQ1から確実に推測できるグループとそれ以外、という分割になり、P1はtake、 P2はそれ以外になるな。
なんかEM法っぽいね。
このやり方だと2グループのケースしかやってないが、確実に独立な物が作れればそれを取り除いて再帰的にやれば良さそうだし、何か工夫もあるかもしれん。
そのあと、この分割方法はexponential timeがかかっちゃうが、もっと効率的に分割を探すアルゴリズムがある、と言って詳細は説明してない。 意外とぬるい本だな。ゆとりには安心。
7.3.1 辞書を使ったambiguation
Vjという物の定義がわかりにくかったのでメモ。(数式はブログのトラブルで出てない。後で直す)
\(V_j\)とwの近いが分かりにくい。 \(V_j\)はw以外の一般の単語、という事か。 例えばcの中の各単語、とか。
すると \(E_{V_j}\) はこの\(V_j\)の辞書での意味のunionか。
例えばTable 7.4では、\(V_j\)は、Thisとかcigarとかburnsとかを表すのかな。 このテーブルには\(E_{V_j}\) は無い気がする。 \(V_j\)と\(D_k\)のunionをカウントしている気がする。
シソーラスを使ったYarowskyのアルゴリズム(Fig 7.5)
7.3.2のYarowskyのアルゴリズム、Figure 7.5の周辺は結講数式の誤植があるな。 これまでもちらほらあったが、ここは特に多い気がする。たぶんKindle版だけだろうが。
\(t_l\)がちょくちょく間違って\(t_1\)と書かれるんだよなぁ。
見れば分かるのだけど、まぁまぁ込み入ってるのでこの手の誤植で気が散ると理解にちょっと苦労する。
またVの大文字と小文字がちょこちょこ間違ってるのは数は少ないがより解読が困難な誤植だな。
Fig 7.5にコードが載ってる。 \(V_j\)と\(T_l\)がなんなのなが鍵と思う。
\(V_j\)は全コンテキストをなめて、単語\(v_j\)が入ってるコンテキストの一覧を集めたもの。
\(T_l\)はコンテキスト\(t_l\)とのスコアがアルファ以上の全コンテキスト。
この2つのインターセクションの濃度は、つまり\(v_j\)の関わるコンテキストと\(t_l\)と近いコンテキストが幾つくらい交わってるかという事。 これを擬似的な同時確率とみなしている訳だよな。
なお、\(t(s_k)\)は意味\(s_k\)のサブジェクトコード。
なかなかこのアルゴリズムは良く出来てる気がする。 1992年にこんな洗練されたアルゴリズムを作ってるとは。やるな、Yarowsky。
7.4 Uesupervised Disambiguation
ここは前のセクションへの参照がいくつかあってメモを取りたくなったのでメモを書く。
7.2.2のBrownらのアプローチ、というのは、情報理論的なアプローチという奴で、訳とコンテキストのグルーピングをEM法っぽく交互に更新していく奴だ。
7.2.1のGaleらのモデル、というのはナイーブベイズの事。
で、ここでやってるのはまんまEM法だな。
Eステップでは単語の仮定された分布でコンテキストが生成される事後分布を求める。
Mステップではこのコンテキストの事後確率を使って単語の分布を再計算する。
Kはどうするのさ、という気がするが、こいつはハイパーパラメータの模様。 それはどうなんだろう。
7章はなかなか良かった
7章読み終わって。なかなか良かった。 アルゴリズムは単純だが現代のアルゴリズムの元となってるのも感じられて、しかもいろいろな記号に慣れる事も出来て、思った以上に勉強になった。
今の時代はword sensのdisambiguationという問題自体あまり扱わない、というかもっとend2endにした方がきっと良いだろうな、という気がするけれど、また将来トレンドが変わる事もあるかもしれないし、またこの問題自体は直接解かなくてもこれらの洞察を反映する事もあるかもしれない。
偶然misreading chatでセンテンスピースの話してて、また菊田さんもbertにセンテンスピースくっつける話してたので元論文を読んだのだが、この時のEM法はこの7章でやってる奴と似ている。 だからこの本でこうした手法に慣れていると読みやすいと思った。
この位なら教養として読んでおいてもいいかな、と思える章だった。 思ったよりも現代でも役に立ちそうね。 序盤の英語の込み入った文法の話は辛いが。
なお、EM法とかは別の所でやってから読む方が良い気がした。 あとの方に解説があるらしいが。 この辺、機械学習そんなやってない人には辛いね。
8章 Lexical Acquisition
lexical acquisitionとはなんぞや?と訳をググってみると、語彙獲得、という訳かな。
lexiconは語彙目録か。
この章の概要
最初に書いてあるのでメモしておく。
まずはlexical acquisitionの手法の評価方法。
次に、
- verb subcategorization
- attachment ambiguity
- selectional preferences
- 単語間のsemantic similarity
をやるとの事。 下2つはいいとして上2つは説明が要りそう。
verb subcategorizationは動詞とその対象との関係、具体的には補語とか目的語とかとの関係というか構造を指すっぽい?
attachment ambiguityはate the cake with…という英語に対してwith以下がate にかかるかcakeにかかるかを判別する、みたいな事。
追記: 8.1はprecisionとかrecallとかの話だった。一応読んだが知らない事は無し。
Kindleの数式誤植
ちょくちょく\(H_0\)とHoが混在したりするのだが、Kindleってなんでこういう数式ミスがあるのが多いのだろう?
数式が出ないならわかるのだが、混在してるという事は\(H_0\)は出る訳で。 見直せばすぐ潰せると思うのだけど、見直す人が居ないのかしら?
それともなんか自動変換的なソフトウェアがあってそれがやってるのかしら?
8.2 Verb subcategorization
なんかあんまり大した事してないので軽く。
何かのCue(手がかり)みたいなのを正規表現とかパターンマッチ的なので決めて、ある動詞について全コーパスで動詞の出現頻度とCueの共起頻度を集計して、Cueの出現頻度から動詞のsubcategorizationの確率を与えて統計の検定をしている。
8.3 attachment ambiguity
前置詞句が動詞にかかるか目的語の名詞にかかるかの議論。
単純に頻度だけでやると句が近いかどうかを無視してしまうので良くない、という話があって、それを改善する為に確率モデル的な扱いをする、という話から8.3.1に入る。
8.3.1 HindleとRooth(1993)
なんかモデルの仮定が特殊なのでメモを残しておく。
前置詞句が複数あった時に最初の前置詞句だけをモデル化したい。 前置詞句は必ず動詞か名詞のどちらかだけに掛かるとする。
そしてランダム変数としては最初かどうかを気にせずにある前置詞pに導かれる句が動詞にかかるかどうかを \(VA_p=1\)で、目的語にかかるかを\(NA_p=1\)で表す。
このpはカウントだけで位置を見ないので、例えば一文にonが2つあると、\(VA_p=1\)はどっちのonかは分からない。
このどっちか分からないランダム変数で最初の前置詞句の確率モデルを考える、というのが変わってる。(簡単化の為と思われる)。
なお、VP NP PP1 PP2という並びでPP1が動詞にかかってPP2が名詞にかかる事は無いらしい。 これをcrossing bracketというとか。 ググってもそれっぽい事は書いてないが、構文のツリーがまたぐのは禁止されてるらしい。へー。
その辺の事を使って、最初のpがNPに掛かる確率は\(VA_p\)に依存しないが、最初のpがVPに掛かる確率は\(NA_p\)に依存する、という非対称性がある。(なお各ランダム変数の条件付き独立は仮定されている)。
あと式でわかりにくいのが、C(v, p)などがここでは共起では無くてpがvにattchされたカウントになってる所。
この頃は課題山積みだな
8.3.2から先程のやり方の問題点をいろいろ挙げているがどれも重要な物ばかりで、これではソフトウェアで解決出来るのはtoy exampleだけでは無いか、という気分になる。
一方でここで述べられている問題の多くについてbertなどの最近のモデルはある程度はアプローチ出来ていて隔世の感がある。
こうして考えると、seq2seqはまだ翻訳のようなマッチングが出来る対象だけにしか使えない分、ここでの問題はまだまだ壁としてたちはだかってた気がする。
transformerモデルは相当エポックメイキングだよなぁ。 bertよりもtransformerとpositional encodeが真のブレークスルーだった気がする。
8.4 Selectional Preferences
動詞がどういうクラスの目的語を好むのか、という問題についての話。
目的語のクラスの事前確率と動詞がgivenの同クラスの条件付き確率のKL divergenceで選好の強さを表現する、とか。ちょっと面白いね。
特定のクラスじゃなくて動詞のpreferenceの強さはこれを目的語のクラスでマージなライズしたもので、Sと呼んでいる。(8.28)
associationはこの動詞のSに対する特定のクラスの寄与みたいな定義になってる(8.29)
8章は興味深いテーマに素朴なやり方
8章を読み終わった印象としては、やろうとしている事はなかなか興味深いが結果としてやっている事は単純過ぎて実用化は遠いな…というもの。
勉強という点ではやってる事は単純なので分かりやすくて良い。
ただ現代的にはこういう事を学習させようとするよりは、DNNにとって必要な事を勝手に学ばせるように設計する方が良さそうだよな。 章末の将来の方向性はpriorとかをもっと織り込む方向を考えてそうだが、現時点ではそちらには未来は無さそうに見える。
ただ将来また何か進展があってこうした事を学習させる日が来る可能性は十分あるので、トピックとして知っておくのは悪くない気がした。
9章 Markov Models
今更HMMの話とかされてもなぁ、という気分だが、一応読んでおく。
9.2 HMMのcrazy soft drink machine
Example 1がわかりにくかったのでメモ。 遷移は買ったあとと書いてあるが式は買う前に遷移してる気がする。 状態をカタカナ、出てくる物をローマ字で書く。
まずコーラからどこに遷移するかで二通り、コーラに留まる場合は0.7で、その時のlemが出てくる確率は0.3。 つまり0.7x0.3
この場合には、次にコーラに留まる場合が0.7、アイスティーになるのは0.3で、その状態でice_tがでてくるのはそれぞれ、0.1、 0.7なので、
「最初がコーラに留まる場合」
- 0.7x0.3x0.7x0.1
- 0.7x0.3x0.3x0.7
次に最初にアイスティーに遷移する場合、その遷移は0.3で、さらにその状態でlemが出てくるのは0.2。 さらにそこから留まるのが0.5で起こってその場合のice_tは0.7で起こる。 コーラへの遷移は0.5でこの場合ice_tは0.1。
「最初にアイスティーに遷移する場合」
- 0.3x0.2x0.5x0.7
- 0.3x0.2x0.5x0.1
あれ?回答間違ってない?
では買った後に遷移するとしてみよう。 すると最初のlemは0.3だ。
そして
- 0.7でコーラに留まってその場合のice_tは0.1
- 0.3でアイスティーに遷移してその場合は0.7
となる。以上を合わせると、
- 0.3x0.7x0.1
- 0.3x0.3x0.7
となる。 これはよく見ると答えを変形したものになってるな。 わかりにくいが、買ったあとの状態で場合分けしてるのか。それは出てくる物には影響を与えないので足すといつも1になる。例えば最初2つの式は、
- 0.7x0.3x0.7x0.1+0.7x0.3x0.3x0.1
は、以下のようにくくれるという事。
- 0.7x0.3x(0.7+0.3)x0.1
買った後の遷移を先に書くのでなお一層分かりにくいが、答えはあってた。 なんでこんな分かりにくい書き方してるかは分からないが、あとで一般的なケースがこう書ける、とかなのかなぁ。
追記: そうっぽい。遷移の間で文字がemitされる、と考えるのが良いらしい。先に説明が欲しいな…
9.2.1のn-gramのinterpolationの例が分からん
\(\lambda_iab\) が何を表すのかいまいち分からん。なんだろ?これ。
遷移図を見ていると、\(\lambda_1\)でユニグラムに行く訳だよな。 これ以外のパラメータが要る気がしないのだが。
Errata見ても無いし、ググッても誰も何も言ってない。うーん、分からん。
まぁいいや。孤の\(\lambda_1\)とかが、\(\lambda_1ab\)と書く気の誤植だった、と考えて先に進もう。
9.3 HMMで知りたい3つの問題
この節の構成に対応してそうなのでメモしておく。
- モデルが与えられた時に、ある観測が得られる確率
- モデルと観測が与えられた時にもっとも良いhidden stateの系列を選ぶ方法
- 観測データからモデルのパラメータの推計
違う書き方をしてるがようするにこういう事だろう。
fowardとbackward procedureのメモ
つらつら読んでたらベータの定義が分からなくなったのでメモしておく。
\(\beta_i(t)\)は、tの時点でstateがiの時に、tよりあとの観測が得られる確率。 暗黙にoのtからTまでは固定されている。 oの特定の系列の確率を求める問題なので。
ついでにアルファもメモしておこう。 \(\alpha_i(t)\)は、1からt-1までの観測が指定されたoの系列で、かつtの時点で状態がiになる確率。
Table 9.2のforwardとbackward をやってみる
こういうのは自分で計算してみないとね。 という事でやってみよう。
まず問題で使う図9.2とかテーブルを書いておくか。
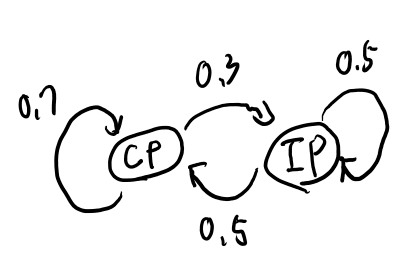
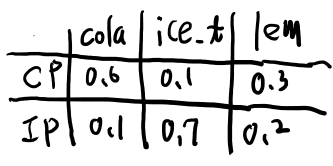
で、lem, ice_t, colaが得られる確率だ。
これをまずforward procedureで計算する。 \(\alpha_CP(1)\)は1だ。
で、2に行く時に今回はlemがemitされる。
2の状態として考えられるのはCPとIP。
CPには0.7の確率で行き、lemは0.3で得られる。
IPは0.3の確率で行き、lemは0.2。
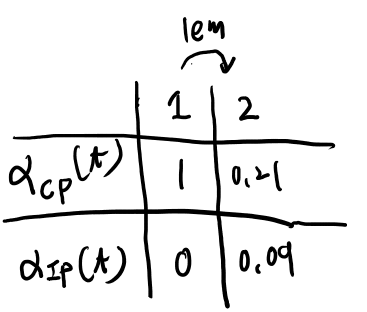
なるほど、するとtが3の時を考える時には、前の状態との関係とこの\(\alpha_i(t)\)だけでわかるのか。 というのはその状態まで来る全てのパスは既に計算されているから。
もう理解したから続きはやらんでいいか。 なんかこの計算、前もやったなぁ。
9.3.2 Viterbiアルゴリズムでhidden state を推計
毎回忘れるViterbiアルゴリズム。 今回も忘れてるのでちゃんと追う。
\(\delta_j(t)\)はt時の状態がjになるような、もっともありえそうなt-1までの系列を保存した物。
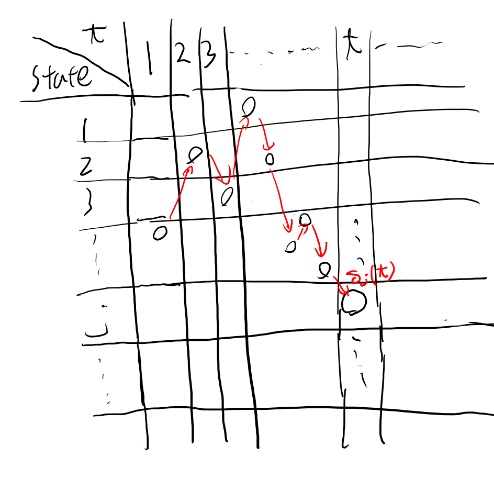
あるtの時点を考えると、その時点での状態はN個あるのでデルタもN個ある。 それぞれの状態での、そこにいたる最大の確率のパスだけ覚える。
そしてその次のt+1時点の状態を考える。 例えばkの状態を考える。 kの状態になる最大のパスは、t時からの遷移の確率とそこまでの系列のでやすさの両方に依る。 例えばt期のjからt+1期のkになる確率を考える。
t期にjが出るもっとも出やすい確率はデルタで与えられているので、そのjからt+1期にkへと遷移する確率を掛ければ、jからやってくる一番高い確率となる系列は出てくる。
遷移の確率は\(b_{ { j k { o_t} }}\)となる。
t+1期にkである為にはt期のどれかの状態から遷移する必要はあるので、上記の計算を全状態について行えば、その最大値が\(\delta_k(t+1)\)となる。
\(\Psi_j(t+1)\)は、この最大の系列が分かった後にある状態から一つ前にたどる為の、一つ前の状態を覚えておくもの。 t+1期に状態jとなる、もっとも確率の高い系列の、t期の状態。
この\(\Psi_j(t+1)\)を一つずつ遡っていけば、このもっとも実現確率の高い系列の状態列を得る事が出来る。
Viterbiアルゴリズム、手計算してみよう
やはり自分で計算しないと分からないので、手で求めてみる。 まずは\(\delta_j(1)\)を事前分布で初期化。 この場合はCPと知ってるので、\(\delta_CP(1)\)が1でIPの方が0か。 プサイはこの時点では無い。
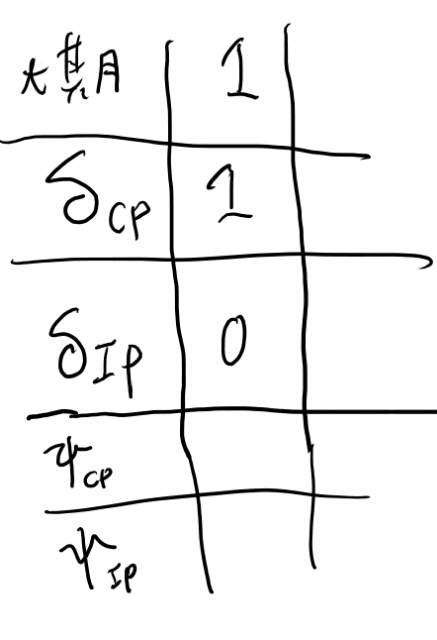
次に\(\delta_CP(2)\)を求めよう。 CPから遷移して2になりつつlemをemitする確率は、そもそも前の状態はCPしか無いので、0.7x0.3か。
次に\(\delta_IP(2)\)を求めてみよう。 これも前の状態はCPしか無いので、遷移の0.3にlemをemitする確率を掛けて、、、ってemitする時点ではCPなのでこの場合も0.3か。つまり0.3x0.3だな。
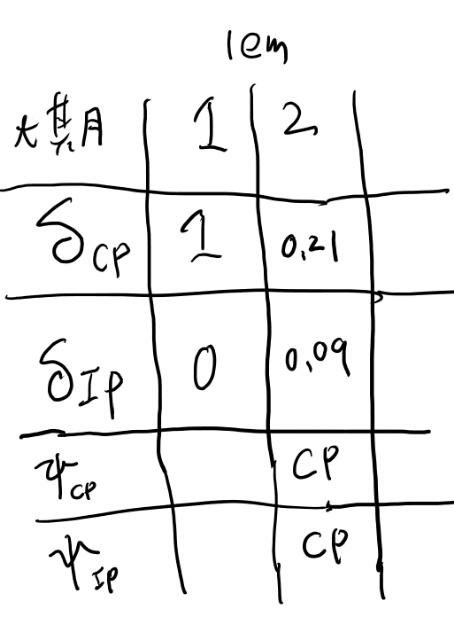
次に\(\delta_CP(3)\)を求めよう。 3でCPに遷移しつつice_tを出す確率を考える。 前がCPの場合とIPの場合の確率を別々に出して大きい方を採用だな。
前がCPの場合、 0.21x0.1x0.7だな。つまり0.0147か。
前がIPの場合、0.09x0.7x0.5だな。 つまり0.0325か。
という事は\(\delta_CP(3)\)0.325で、IPから来たケースだな。
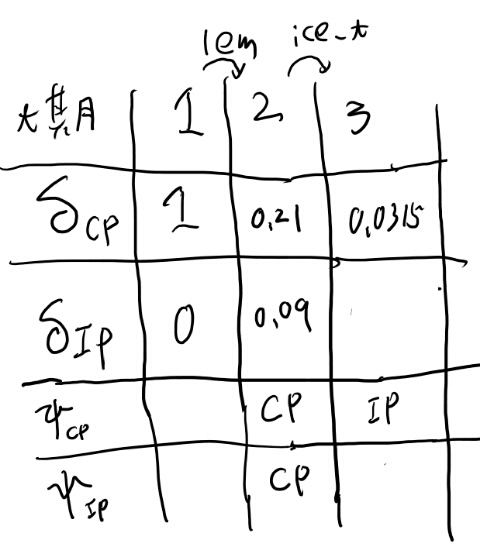
なるほど、プサイは前のどのデルタを見ればいいのかを教えてくれる訳か。
次に\(\delta_IP(3)\)を求めよう。
前がCPの場合、0.21x0.1x0.3で、0.0063。
前がIPの場合、0.09x0.7x0.5で、0.0315。 お、前がIPの方が高いね。表を埋めよう。
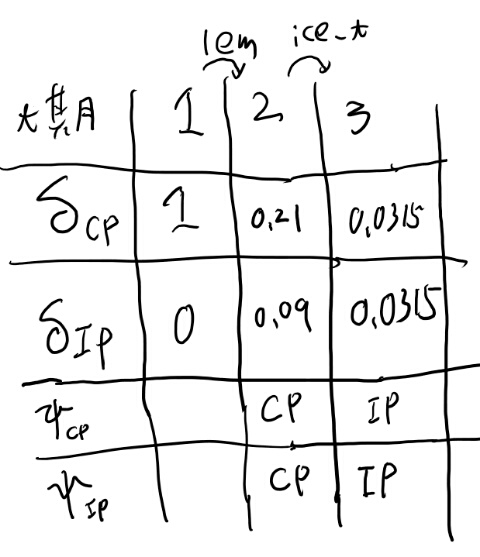
よし、だいたい理解出来たぜ。
最大のパスを覚えていくだけだと、遷移確率が凄い低い状態の観測が出た時にまずい。 だが一つ前の全状態について、そこまで来る最大のパスを覚えておけば、そこまでの実現確率はやや低めでもそこからの遷移の確率が高いパスへと移行出来る、という事だ。
まぁまた半年後には忘れてるんだろうが。
9.3.3 パラメータ推計
EM法で求める、という話なのだけど、Kindle版は数式のレイアウトがちょっと壊れてて分かりにくいのでメモを書いておく。
まず、\(p_t(i, j)\)は与えられた観測で、t期にi、t+1期にjを通る確率。
そしてresponsibilityだっけ?\(\gamma_i(t)\)。 これは\(p_t(i, j)\)をjでマージナライズしたものとなっている。 つまりt期にiを通る期待値だな。
で、パラメータのアップデートの手順は
- パラメータをなんかに決める
- そのパラメータで\(\alpha_i(t)\)と\(\beta_i(t)\)を計算する
- \(\alpha_i(t)\)と\(\beta_i(t)\)と最初に決めたパラメータを使って\(p_t(i, j)\)を求める
- 各期で\(p_t(i, j)\)のjをマージナライズして\(\gamma_i(t)\)を求める
- 4で求めた2つを使ってパラメータを更新
- 更新されたパラメータでまた1からやる
という手順になる。5のパラメータの更新は教科書の9.17, 9.18, 9.19を使えば良い。 この式の解釈を考えてみる。
まず事前分布の更新には\(\gamma_i(1)\)を使うと言っている。 これは1期にiを通り2期にjを通る確率を、全jについて足し合わせたものだ。 この\(p_t(i, j)\)をどう求めたかというと、backward procadureで\(\beta_i(t+1)\)を求めて、元のパラメータである事前分布と遷移確率を\(\beta_i(t+1)\)とあわせて求める。
遷移と事前分布は所与として、実際に観測されたデータに合うt+1期の状態の分布の推計が\(\beta_i(t+1)\)だな。
なかなか難しいな。図を描いてみよう。
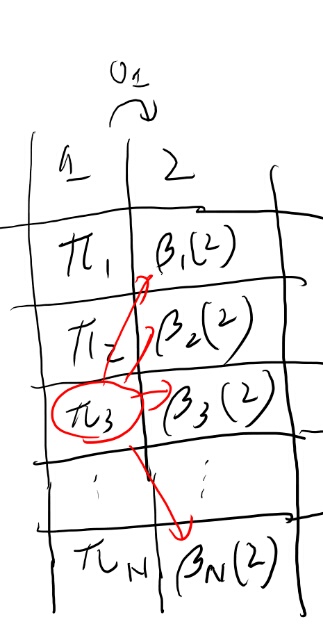
うーむ、よく分からんな。素直にベイズルールで直接求めてみよう。
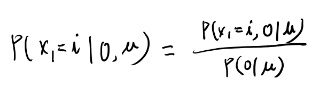
なんかこのまま行くとEM法を証明する、みたいな話になっちゃうよなぁ…
間違った方向に進んでる気がするが、少しこのまま計算してみよう。
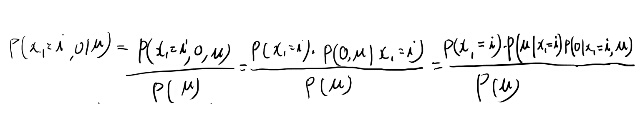
パラメータの事後分布の意味する物は良くわからないが、分子の最後の項は\(x_1\)がiの時に観測が得られる確率だよな。それはiから2期まで遷移して\(o_1\)が出る確率と遷移する確率を全部足し合わせた物で、それはまさに\(\gamma_i(1)\)の式の分子のアルファより先の項が表すものか。
パラメータの事後分布と事前分布の比がなんなのかは良く分からないが、これを1と近似すれば更新式9.17になってそう。
PRMLのEM法を読み直す
なんか良く理解できないので、PRMLの9.3あたりを読み直そう。 バラメータとhidden stateがある時に観測結果の尤度を最大化するパラメータを選ぶ、という話。
今回はhidden stateはそのままHMMの各stateと解釈出来る。これをZと呼んでる。
- E-step 古いパラメータを使ってZの分布を求める
- M-step Qを最大化する新しいパラメータを求める。Qは以下の式
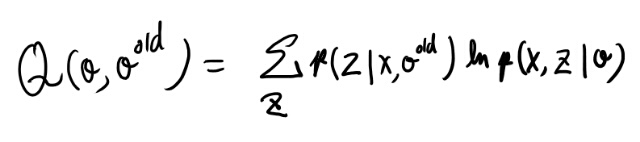
古いパラメータと観測結果からZの分布を求める、というのは、アルファとベータの計算に対応していそう。 XとZの同時確率はどうなっているのか? Viterbiアルゴリズムで求めた最適経路での確率だよな。
で、このパラメータの更新式は13章で計算してたはず、とp617を読み直すと、Exercise 13.5になってる、、、 仕方ない、まず解いてみよう。
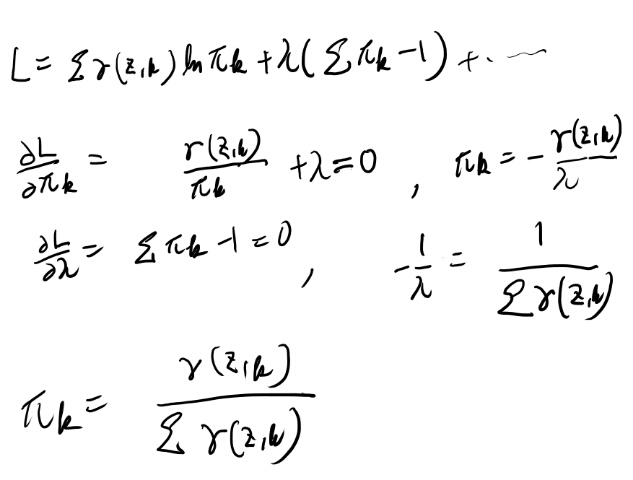
このガンマというのはXと古いパラメータの元での\(z_n\)がk を取る確率だな。 ってそれが知りたいんだよ。ぐぬぬ。
13章をもう少し読み直してみた。p621の13.37が今知りたい事と同じ話をしている。 この話を元に、サイコロ本のノーテーションで書いてみよう。
パラメータが既知だとすると、同時確率は以下のように表される。
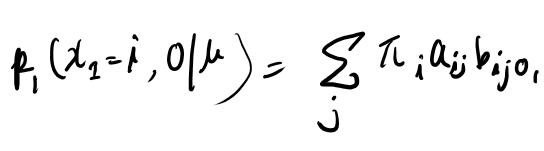
ここでこのパラメータは自由に動くパラメータ。 次に古いパラメータでのhidden stateの分布を求める。この2つがあればQが求まるので、あとはこれをラグランジュの未定定数法で解けるのは先程やった通りだ。
古いパラメータでのhidden stateの分布というのは、式としては以下を求めたい。
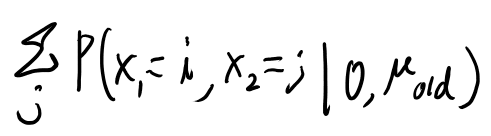
お?これは見覚えがあるな。 \(\gamma_i(1)\)か。
つまりこれは、古いパラメータで1期のhidden stateを推計したものだな。
それは一見すると\(\pi_i\)に思えるのがややこしい所だが、それは事後確率では無い。観測を得たあとの事後確率は、まさに9.16でやってる変形だな。
お、全てを理解した。 \(a_{ { i j }}\)と\(b_{ { i j { o_t} }}\)の更新式はPRMLの13.17式に相当する物を出してラグランジュの未定定数法で解く必要があるが、これはやれば出来るだろうからもういいか。
一応感覚的な解釈はしておく。
9.18は、各tでのiからjに遷移する確率を、tについて平均を取ってるのだろうな。 分母の\(\gamma_i(t)\)は、ようするに状態iになる確率。分子はiからtへの遷移が起こる確率。 その比を取ると、iという状態を所与とした時にjへと遷移する確率の平均が得られる。
9.19はi, jの遷移が起きた時にkがemitする確率を求めていて、これはi, j遷移が起きる確率と、i, j遷移が起きてなおかつkがemitする確率の比となるので、それをそのまま計算している。
どちらも感覚的には分かりやすいが、これが何をしているかはちゃんとEM法の枠組みで考えないとわかった気がしながら全然分かってない、となりがちなので注意だな。
9章、勉強にはなったがこの本単体では分からん
読み終わったので感想。 HMMに実際の数字をあてはめて手計算出来る。これは素晴らしい。
ただ、EM法の解説が後に回されていて結果だけ使われているので、解説は理解できないと思う。 しかもその最終結果が感覚的には分かる気がするのがタチが悪い。 どちらのパラメータを使った何を求めているのか、を相当気をつけて読まないと理解出来ないが、その辺の解説が無い。
ただ、PRML片手に復習として読むと詳しく書かれているし、何より実際の数字と答えがあるのは良いね。 計算してみて理解を深める事が出来る。 HMMの解説としてもすっきりとした構成で、昔理解したことをちゃんと整理して思い出すのに良い。
という事で最初に読む本としてはいまいちだな、と思うが、EM法を一度どこかでちゃんと勉強した人にとっては良い内容だと思った。
10章 Part of Speech tagging
この本の時点でaccuracyが96%から97%と言ってるので現在はどのくらい行くのかな? とググったが、あんま変わってないな。 まぁこのタスク自体をそんな真剣に取り組む人が減ったのだとは思うが。 transformer型のモデルではやってなさそうだし。
10.2.1 Markov Model Taggersの確率モデル
教師データとしてPoSタグがあり、PoSタグからemitする確率は他に依存せず決まる、さらにPoSタグは一つ前のPoSタグにしか依存しない、という前提でHMMのパラメータを推計する。
HMMといいつつPoSが単なるバイグラムなので、単にカウントするだけでPoSの遷移確率は決まる。 PoSのタグがついているので、emitされる単語の分布も単に特定のPoSタグの遷移を全部探して、そこでemitする単語を数えるだけ。
タグの遷移の確率とemitする確率がテーブルとして得られたら、あとはテストセットに対しては単語の列からタグの列を、10.7式に従い決める事が出来る。 といってもこのargmaxはそんな簡単では無い。Viterbiアルゴリズムが要る奴やね。
10.4 Transformaiton based tagging
各単語のもっとも確率の高いタグをまず適用し、そのあとtransformationのルールを適用して修正していく。 このtransformationのルールのうちどれを適用するかの順番を学習するっぽい。
transformationのルール自体は人間が与えるのかな?それだとがっかりだが。>そうっぽい
10章は9章の応用っぽい
9章をちゃんと理解していると、10章はあまり難しい所は無い。 HMMの練習問題のような気持ちで読めるし、9章の理解が深まって良い。
一方でこのタギング、流行ったのは伝わってくるが、いまいち必要性に説得力が無いな。 最後の方でpartial parsingは結局タグ使わずに生のテキスト使う方が精度が良い、とか言われてしまうと。
この頃はNLPの実アプリケーションへの応用は凄く大変で、ちょっとの応用しかなかったのだろうなぁ、と歴史に思いを馳せる、みたいな内容になってしまってる。
11章から先
ファイル大きすぎと言われたので分割。